Колебания. Свободные колебания. Параметры, описывающие колебательное движение. Гармонические колебания, уравнение гармонических колебаний

Колебания – явления или процессы, имеющие ту или иную степень повторяемости во времени.

Свободные колебания – колебания в системе, возникающие после выведения ее из положения равновесия.

Условия возникновения свободных колебаний: 1) наличие у системы положения устойчивого равновесия; 2) возникновение возвращающей силы, направленной к положению равновесия; 3) малое трение.

Параметры, описывающие колебательное движение:

1. Период (Т) – время одного полного колебания (измеряется в секундах).

2. Частота (ν) – физическая величина, показывающая, сколько полных колебаний система совершает в единицу времени (измеряется в Гц (1Гц = с^-1)).

3. Циклическая частота колебаний (ω) – физическая величина, показывающая, сколько полных колебаний система совершает за 2π секунд (измеряется в Гц).

4. Амплитуда (х_m или S_m) – максимальное отклонение системы от положения равновесия (измеряется в метрах).

5. Мгновенное значение отклонения системы от положения равновесия (х или S) – отклонение системы от положения равновесия в данный момент времени (измеряется в метрах).

Зависимости между параметрами: ; .

Гармонические колебания – колебания, происходящие по закону синуса или косинуса.

Уравнение гармонических колебаний:

, где x– мгновенное отклонение от положения равновесия, х_m – амплитуда, ω_о – циклическая частота свободных колебаний, ν_о – частота свободных колебаний, Т – период колебаний, φ_о – начальная фаза колебаний, – фаза колебаний.

Фаза колебаний – физическая величина, определяющая положение колеблющегося тела в какой-либо определенный момент времени (измеряется в радианах).

Начальная фаза колебаний – физическая величина, определяющая положение колеблющегося тела в начальный момент времени (t = 0).

Математический и пружинный маятники (дифференциальное уравнение их колебаний, решение дифференциального уравнения, скорость, ускорение, частота и период колебаний). Потенциальная, кинетическая и полная энергия колебаний маятника; их зависимость от времени. Превращение энергии при колебательном движении

Математический маятник – материальная точка, подвешенная на невесомой и нерастяжимой нити.

Дифференциальное уравнение колебаний математического маятника:

, где ω_о – циклическая частота колебаний (, где g – ускорение свободного падения, ℓ – длина нити (подвеса)), S – смещение маятника из положения равновесия (длина дуги), а_τ – ускорение маятника вдоль касательной к траектории в данной точке (тангенциальное ускорение).

Решение дифференциального уравнения:

, гдеS_m – амплитуда колебаний.

Скорость маятника изменяется со временем по закону: ,где = ω₀S_m – амплитудное (максимальное) значение скорости маятника.

Тангенциальное ускорение маятника изменяется со временем по закону: , где 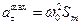– амплитудное (максимальное) значение ускорения маятника.

Формулы для расчета частоты ν ₀ и периода Т колебаний математического маятника:

.

Период колебаний математического маятника не зависит от: 1) массы подвешенной материальной точки; 2) амплитуды.

Формулы для расчета потенциальной Е_р и кинетической Е_к энергий математического маятника: , , где m – масса подвешенной материальной точки.

Формула для расчета полной механической энергии математического маятника: .

Пружинный маятник – тело, скрепленное с пружиной.

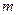Дифференциальное уравнение колебаний пружинного маятника: , где – ускорение тела вдоль координатной оси х, – циклическая частота колебаний маятника ( – жесткость пружины, – масса тела, скрепленного с пружиной), х – смещение маятника из положения равновесия (вдоль прямой).

Решение дифференциального уравнения:

, где –амплитуда колебаний.

Скорость маятника изменяется со временем по закону:

,где = ω_ox_m – амплитудное (максимальное) значение скорости маятника.

Ускорение маятника изменяется со временем по закону:

, где – амплитудное (максимальное) значение ускорения маятника.

Формулы для расчета частоты ν ₀ и периода Т колебаний пружинного маятника:

; .

Период колебаний пружинного маятника зависит от: 1) массы скрепленного с пружиной тела; 2) жесткости пружины.

Формулы для расчета потенциальной Е_р и кинетической Е_к энергий пружинного маятника: ; ,где 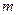– масса подвешенной материальной точки.

Формула для расчета полной механической энергии пружинного маятника:

Превращения механической энергии при колебаниях математического и пружинного маятников: 1) каждые четверть периода потенциальная энергия превращается в кинетическую и обратно; 2) в любой момент времени сумма потенциальной и кинетической энергии маятника (полная энергия колебаний) неизменна.

Date: 2016-06-09; view: 615; Нарушение авторских прав