Первый закон Ньютона. Инерциальные системы отсчета. Принцип относительности Галилея, преобразования Галилея

I закон Ньютона: существуют такие системы отсчета, относительно которых поступательно движущееся тело сохраняет свою скорость неизменной, если на него не действуют другие тела или действие других тел скомпенсировано.

Инерциальные системы отсчета – системы отсчета, в которых выполняется I закон Ньютона.

Любая система отсчета, движущаяся равномерно прямолинейно относительно данной инерциальной системы отсчета, также является инерциальной.

Принцип относительности Галилея: все механические явления протекают одинаково во всех инерциальных системах отсчета.

Инерция – явление сохранения скорости тела (состояния покоя) при отсутствии внешних воздействий на тело или при их компенсации.

Преобразования Галилея:

1. Преобразование координат (связь между координатами x, y, z некоторой точки P в системе отсчета К и координатами x', y', z' этой же точки в системе отсчета К', движущейся относительно системы К с постоянной скоростью так, что координатные оси xи x' обеих систем отсчета совпадают, а оси у и y', а также z и z' параллельны друг другу):

х = х' + ut; y = y'; z = z', где x', y', z' – координаты точки относительно подвижной системы отсчета; x, y, z – координаты точки относительно неподвижной системы отсчета; u – скорость подвижной системы отсчета относительно неподвижной.

Предполагается, что отсчет времени (t = 0) начат в тот момент, когда начала координат обеих систем совпадали друг с другом.

2. Преобразование скоростей: 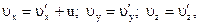где 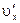– проекция на ось х скорости точки относительно подвижной системы отсчета (системы К'), υ_x – проекция на ось х скорости точки относительно неподвижной системы отсчета (системы К).

3. Одинаковое значение ускорения точки в обеих системах отсчета: а_х = а ' _х.

4. Сохранение длины отрезка: ℓ = ℓ´.

5. Одинаковое течение времени в обеих системах отсчета: Dt = Dt'.

Date: 2016-06-09; view: 1133; Нарушение авторских прав