Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Прогнозное значение определяется путем подстановки в уравнение регрессии соответствующего прогнозного значения Затем вычисляется средняя стандартная ошибка прогноза
|
|
где 
и строится доверительный интервал прогноза
Интервал может быть достаточно широк за счет малого объема наблюдений.
Регрессии, нелинейные по включенным переменным, приводятся к линейному виду простой заменой переменных, а дальнейшая оценка параметров производится с помощью МНК.
Гиперболическая регрессия: 
Линеаризующее преобразование: 
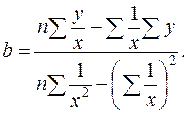
Регрессии, нелинейные по оцениваемым параметрам, делятся на два типа: внутренне нелинейные 
и т.п. (к линейному виду не приводятся) и внутренне линейные (приводятся к линейному виду с помощью соответствующих преобразований), например:
Экспоненциальная регрессия: 
Линеаризующее преобразование: 
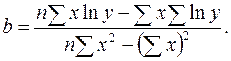
Степенная регрессия: 
Линеаризующее преобразование: 
Показательная регрессия: 
Линеаризующее преобразование:
Логарифмическая регрессия: 
Линеаризующее преобразование: 
2. Решение типовых задач
Пример 1.1. По 15 предприятиям отрасли (табл. 1.1) известны: 
– объем произведенной продукции (тыс. ед.) и 
– затраты на выпуск этой продукции (тыс. ден. ед.). Необходимо:
1) определить зависимость от 
2) построить корреляционные поля и график уравнения линейной регрессии на
3) сделать вывод о качестве модели и рассчитать прогнозное значение при прогнозном значении 
составляющем 107% от среднего уровня.
Таблица 1.1
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| x | 2,7 | 1,5 | 8,2 | 4,5 | 3,3 | 5,8 | 3,0 | 7,1 | 1,2 | 10,4 | 4,9 | 5,2 | 11,5 | 9,4 | 6,5 |
| y |
Решение:
1) В Excel составим вспомогательную таблицу 1.2.
Таблица 1.2
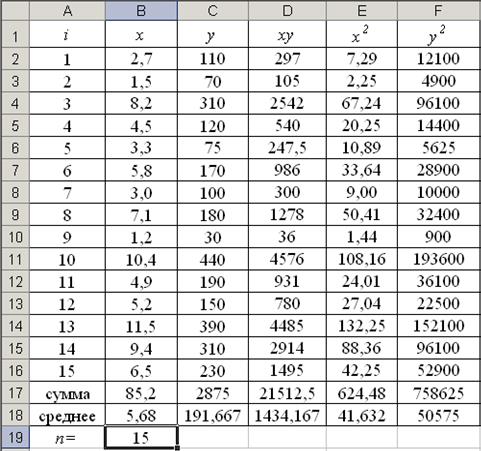
Вычислим количество измерений 
Для этого в ячейку В19 поместим = СЧЁТ(A2:A16).
С помощью функции ∑ (Автосумма) на панели инструментов Стандартная найдем сумму всех (ячейка В17) и (ячейка С17).
Вычислим выборочные средние: 
=5,68;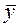 
=191,67. Таким образом, средний объем произведенной продукции по 15 предприятиям отрасли составляет 5,68 тыс. ед., а средние затраты на выпуск этой продукции – 191,67 тыс. ден. ед.
Заполним столбцы D, E, F. Например, в ячейку D2 поместим = B2*C2, затем на клавиатуре нажмем ENTER. Щелкнем левой кнопкой мыши по ячейке D2 и, ухватив за правый нижний угол этой ячейки (черный плюсик), потянем вниз до ячейки D16. Произойдет автоматическое заполнение диапазона D3 – D16.
Для вычисления в ыборочной ковариации между и используем формулу 
т.е. в ячейку B21 поместим = D18-B18*C18 и получим 345,5 (рис. 1.1).
Выборочную дисперсию для найдем по формуле 
т.е. в ячейку B22 поместим = E18-B18*B18 и получим 9,37 (рис. 1.1). Аналогично определяем 
=13838,89.
Рис. 1.1. Решение примера 1.1 в Excel
Выборочный коэффициент корреляции 
=0,96 очень высокий, что указывает на прямую и весьма сильную связь между и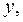 
т.е. с ростом объема произведенной продукции 
увеличиваются затраты на выпуск этой продукции 
Выборочный коэффициент линейной регрессии 
=36,87; параметр 
=-17,78. Значит, уравнение парной линейной регрессии имеет вид 
=-17,78+36,87 
Коэффициент 
показывает, что при увеличении объема произведенной продукции на 1 тыс. ед. затраты на выпуск этой продукции 
в среднем увеличатся на 36,87 тыс. ден. ед.
2) Подставляя в найденное уравнение регрессии фактические значения определим теоретические (расчетные) значения в столбце G.
С помощью Мастера диаграмм строим корреляционные поля (выделяя столбцы со значениями и ) и уравнение линейной регрессии (выделяя столбцы со значениями и ). Выбираем тип диаграммы – Точечная и, следуя рекомендациям Мастера диаграмм, вводим нужные параметры (название, подписи к осям, легенду и т.п.). В результате получим рис. 1.2.
Рис. 1.2. График зависимости объема произведенной продукции
от теоретических и фактических затрат на выпуск этой продукции
3) Для оценки качества построенной модели регрессии вычислим:
• коэффициент детерминации 
=0,92, который показывает, что изменение затрат на выпуск продукции на 92% объясняется изменением объема произведенной продукции 
а 8% приходится на долю неучтенных в модели факторов, что указывает на качественность построенной регрессионной модели;
• среднюю ошибку аппроксимации. Для этого в столбце H вычислим 
а в столбце I – выражение 
(рис. 1.1). При умножении среднего значения (ячейка I18) на 100% получим 
18,2%. Следовательно, в среднем теоретические значения отклоняются от фактических на 18,2%.
С помощью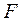 
-критерия Фишераоценим значимость уравнения регрессии в целом: 
150,74.
На уровне значимости 0,05 
=4,67 определяем по таблице 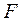-критерия Фишера (таблица 1 приложения) либо с помощью встроенной статистической функции FРАСПОБР (рис. 1.3).
Так как 
то уравнение регрессии значимо при 
=0,05.
Рис. 1.3. Диалоговое окно функции FРАСПОБР
Средний коэффициент эластичности 
=1,09 показывает, что с ростом объема произведенной продукции на 1% затраты на выпуск этой продукции в среднем по совокупности возрастут на 1,09%.
Рассчитаем прогнозное значение 
путем подстановки в уравнение регрессии =-17,78+36,87 
прогнозного значения фактора 
= 
1,07=6,08. Получим =206,33. Следовательно, при выпуске продукции в количестве 6,08 тыс. ед. затраты на производство этой продукции составят 206,33 тыс. ден. ед.
Найдем 
=35,606 поместив в ячейку F23 = КОРЕНЬ(J17/(B19-2)).
Средняя стандартная ошибка прогноза:
=36,79.
На уровне значимости =0,05 либо по таблице 
- критерия Стьюдента (таблица 2 приложения) либо с помощью встроенной статистической функции СТЬЮДРАСПОБР определим 
=2,1604 и вычислим предельную ошибку прогноза, которая в 95% случаев не будет превышать 
=79,48.
Доверительный интервал прогноза:
206,33-79,48 
206,33+79,48 или 126,85 285,81.
Выполненный прогноз затрат на выпуск продукции оказался надежным (1-0,05=0,95), но неточным, так как диапазон верхней и нижней границ доверительного интервала составляет 
=2,25 раза. Это произошло за счет малого объема наблюдений.
3. Решение задач с помощью электронных таблиц Excel
Решение эконометрических задач можно упростить, используя встроенные функции. Активизируем Мастер функций любым из способов:
• в главном меню выбрать Вставка / Функция;
• на панели инструментов Стандартная щелкнуть по кнопке 
Вставка функции.
Для вычисления выборочных средних используем функцию СРЗНАЧ(число1:числоN) из категории Статистические.
Выборочная ковариация между и находится с помощью функции КОВАР(массив X;массив Y) из категории Статистические.
Выборочные дисперсии определяются статистической функцией ДИСПР(число1:числоN).
Выборочный коэффициент корреляции между и вычисляется с помощью статистической функции КОРРЕЛ(массив X;массив Y).
Параметры линейной регрессии 
в Excel можно определить несколькими способами.
1 способ) С помощью встроенной функции ЛИНЕЙН. Порядок действий следующий:
1. Выделить область пустых ячеек 5x2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики или область 1x2 – для получения только коэффициентов регрессии.
2. С помощью Мастера функций среди Статистических выбрать функцию ЛИНЕЙН и заполнить ее аргументы (рис. 1.4):
Рис. 1.4. Диалоговое окно ввода аргументов функции ЛИНЕЙН
Известные_значения_y – диапазон, содержащий данные результативного признака Y;
Известные_значения_x – диапазон, содержащий данные объясняющего признака X;
Конст – логическое значение (1 или 0), которое указывает на наличие или отсутствие свободного члена в уравнении; ставим 1;
Статистика – логическое значение (1 или 0), которое указывает, выводить дополнительную информацию по регрессионному анализу или нет; ставим 1.
3. В левой верхней ячейке выделенной области появится первое число таблицы. Для раскрытия всей таблицы нужно нажать на клавишу <F2>, а затем – на комбинацию клавиш <CTRL> + <SHIFT> + <ENTER>.
Дополнительная регрессионная статистика будет выведена в виде (табл. 1.3):
Таблица 1.3
| Значение коэффициента
| Значение коэффициента 
|
| Среднеквадратическое отклонение
| Среднеквадратическое отклонение
|
Коэффициент детерминации 
| Среднеквадратическое отклонение
|
 -статистика 
| Число степеней свободы |
| Регрессионная сумма квадратов | Остаточная сумма квадратов |
В результате применения функции ЛИНЕЙН получим:
| 36,87 | -17,78 |
| 3,003 | 19,379 |
| 0,9206 | 35,606 |
| 150,74 | |
| 191102,48 | 16480,9 |
(2 способ) С помощью инструмента анализа данных Регрессия можно получить результаты регрессионной статистики, дисперсионного анализа, доверительные интервалы, остатки, графики подбора линий регрессии, графики остатков и нормальной вероятности. Порядок действий следующий:
1. Необходимо проверить доступ к Пакету анализа. Для этого в главном меню нужно выбрать Сервис / Настройки и напротив Пакета анализа установить флажок.
2. Выбрать в главном меню Сервис / Анализ данных / Регрессия и заполнить диалоговое окно (рис. 1.5):
Входной интервал Y – диапазон, содержащий данные результативного признака Y;
Входной интервал X – диапазон, содержащий данные объясняющего признака X;
Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Константа-ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении;
Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;
Новый рабочий лист – можно задать произвольное имя нового листа, на который будут выведены результаты.
Для получения информации об остатках, графиков остатков, подбора и нормальной вероятности нужно установить соответствующие флажки в диалоговом окне. В результате получим итоги как на рис. 1.6.
Рис. 1.5. Диалоговое окно ввода параметров инструмента Регрессии
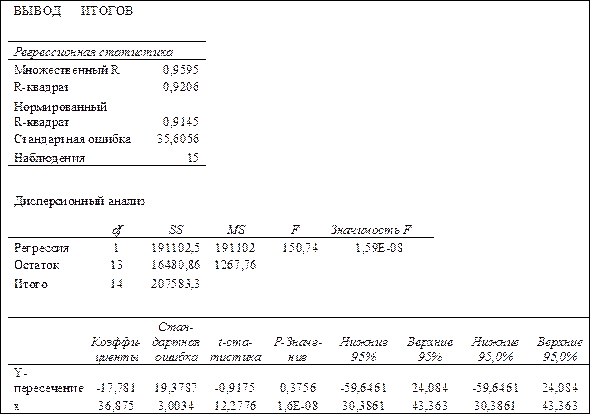
Рис. 1.6. Результаты применения инструмента Регрессия
В Excel линия тренда может быть добавлена в диаграмму с областями гистограммы или в график. Для этого:
1. Необходимо выделить область построения диаграммы и в главном меню выбрать Диаграмма / Добавить линию тренда.
2. В появившемся диалоговом окне (рис. 1.7) выбрать вид линии тренда и задать соответствующие параметры.
Рис. 1.7. Диалоговое окно типов линии тренда
Для полиноминального тренда необходимо задать степень аппроксимирующего полинома, для линейной фильтрации – количество точек усреднения.
Выбираем Линейная для построения уравнения линейной регрессии.
В качестве дополнительной информации можно показать уравнение на диаграмме и поместить на диаграмму величину 
установив соответствующие флажки на закладке Параметры (рис. 1.8).
В результате получим линейный тренд (рис. 1.9).
Рис. 1.8. Диалоговое окно параметров линии тренда
Рис. 1.9. Линейный тренд
Нелинейные модели регрессии иллюстрируются при вычислении параметров уравнения 
с применением выбранной в Excel статистической функции ЛГРФПРИБЛ. Порядок вычислений аналогичен применению функции ЛИНЕЙН.
Ii. Модель множественной регрессии
1. Основные определения и формулы
Множественная регрессия – регрессия между переменными и 
т.е. модель вида: 
где – зависимая переменная (результативный признак);
– независимые объясняющие переменные;
– возмущение или стохастическая переменная, включающая влияние неучтенных в модели факторов;
– число параметров при переменных 
Основная цель множественной регрессии – построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также совокупное их воздействие на моделируемый показатель.
Уравнение множественной линейной регрессии в случае независимых переменных имеет вид 
а в случае двух независимых переменных – 
(двухфакторное уравнение).
Для оценки параметров уравнения множественной регрессии применяют метод наименьших квадратов. Строится система нормальных уравнений:
Решение этой системы позволяет получить оценки параметров регрессии с помощью метода определителей
…, 
где 
– определитель системы;
– частные определители, которые получаются путем замены соответствующего столбца матрицы определителя системы данными правой части системы.
Для двухфакторного уравнения коэффициенты множественной линейной регрессии можно вычислить по формулам:
Частные уравнения регрессии характеризуют изолированное влияние фактора на результат, ибо другие факторы закреплены на неизменном уровне. Эффекты влияния других факторов присоединены в них к свободному члену уравнения множественной регрессии. Это позволяет на основе частных уравнений регрессии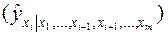 
определять частные коэффициенты эластичности:
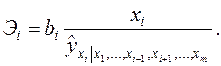
Средние коэффициентами эластичности показывают на сколько процентов в среднем изменится результат при изменении соответствующего фактора на 1%:
Их можно сравнивать друг с другом и соответственно ранжировать факторы по силе их воздействия на результат.
Тесноту совместного влияния факторов на результат оценивает коэффициент (индекс) множественной корреляции:
Величина индекса множественной корреляции лежит в пределах от 0 до 1 и должна быть больше или равна максимальному парному индексу корреляции: 
Чем ближе значение индекса множественной корреляции к 1, тем теснее связь результативного признака со всем набором исследуемых факторов.
Сравнивая индексы множественной и парной корреляции, можно сделать вывод о целесообразности (величина индекса множественной корреляции существенно отличается от индекса парной корреляции) включения в уравнение регрессии того или иного фактора.
При линейной зависимости совокупный коэффициент множественной корреляции определяется через матрицу парных коэффициентов корреляции:
где 
– определитель матрицы парных коэффициентов корреляции;
– определитель матрицы межфакторной корреляции.
Частные коэффициенты корреляции характеризуют тесноту линейной зависимости между результатом и соответствующим фактором при устранении влияния других факторов. Если вычисляется, например, 
(частный коэффициент корреляции между 
и 
при фиксированном влиянии 
), это означает, что определяется количественная мера линейной зависимости между и 
которая будет иметь место, если устранить влияние на эти признаки фактора 
Частные коэффициенты корреляции, измеряющие влияние на фактора 
при неизменном уровне других факторов, можно определить как:
или по рекуррентной формуле:
Для двухфакторного уравнения:
или
Частные коэффициенты корреляции изменяются в пределах от -1 до +1.
Сравнение значений парного и частного коэффициентов корреляции показывает направление воздействия фиксируемого фактора. Если частный коэффициент корреляции получится меньше, чем соответствующий парный коэффициент 
значит взаимосвязь признаков и в некоторой степени обусловлена воздействием на них фиксируемой переменной И наоборот, большее значение частного коэффициента по сравнению с парным свидетельствует о том, что фиксируемая переменная ослабляет своим воздействием связь и 
Порядок частного коэффициента корреляции определяется количеством факторов, влияние которых исключается. Например, – коэффициент частной корреляции первого порядка.
Зная частные коэффициенты корреляции (последовательно первого, второго и более высокого порядка), можно определить совокупный коэффициент множественной корреляции:
Качество построенной модели в целом оценивает коэффициент (индекс) множественной детерминации, который рассчитывается как квадрат индекса множественной корреляции: 
Индекс множественной детерминации фиксирует долю объясненной вариации результативного признака за счет рассматриваемых в регрессии факторов. Влияние других, не учтенных в модели факторов, оценивается как 
Если число параметров при близко к объему наблюдений, то коэффициент множественной корреляции приблизится к единице даже при слабой связи факторов с результатом. Для того чтобы не допустить возможного преувеличения тесноты связи, используется скорректированный индекс множественной корреляции, который содержит поправку на число степеней свободы:
Чем больше величина 
тем сильнее различия 
и 
Значимость частных коэффициентов корреляции проверяется аналогично случаю парных коэффициентов корреляции. Единственным отличием является число степеней свободы, которое следует брать равным 
= 
- -2.
Значимость уравнения множественной регрессии в целом, так же как и в парной регрессии, оценивается с помощью 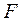- критерия Фишера:
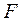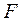Мерой для оценки включения фактора в модель служит частный -критерий. В общем виде для фактора частный -критерий определяется как
Для двухфакторного уравнения частные 
-критерии имеют вид:
Если фактическое значение 
превышает табличное, то дополнительное включение фактора в модель статистически оправданно и коэффициент чистой регрессии 
при факторе статистически значим. Если же фактическое значение меньше табличного, то фактор нецелесообразно включать в модель, а коэффициент регрессии при данном факторе в этом случае статистически незначим.
Для оценки значимости коэффициентов чистой регрессии по 
-критерию Стьюдента используется формула:
где – коэффициент чистой регрессии при факторе 
– средняя квадратическая (стандартная) ошибка коэффициента регрессии 
которая может быть определена по формуле:
При дополнительном включении в регрессию нового фактора коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться. Если это не так, то включаемый в анализ новый фактор не улучшает модель и практически является лишним фактором. Насыщение модели лишними факторами не только не снижает величину остаточной дисперсии и не увеличивает показатель детерминации, но и приводит к статистической незначимости параметров регрессии по -критерию Стьюдента.
При построении уравнения множественной регрессии может возникнуть проблема мультиколлинеарности факторов. Считается, что две переменные явно коллинеарны, т.е. находятся между собой в линейной зависимости, если 
Если факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии. Предпочтение при этом отдается не фактору, более тесно связанному с результатом, а тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами.
Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами. Чем ближе к 0 определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И наоборот, чем ближе к 1 определитель, тем меньше мультиколлинеарность факторов.
Для применения МНК требуется, чтобы дисперсия остатков была гомоскедастичной. Это означает, что для каждого значения фактора 
остатки 
имеют одинаковую дисперсию. Если это условие применения МНК не соблюдается, то имеет место гетероскедастичность. При нарушении гомоскедастичности выполняются неравенства 
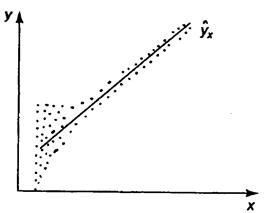
Наличие гетероскедастичности можно наглядно видеть из поля корреляции (рис. 2.1).
а) б)
в)
Рис. 2.1.Примеры гетероскедастичности:
а) дисперсия остатков растет по мере увеличения 
б) дисперсия остатков достигает максимальной величины при средних значениях переменной и уменьшается при минимальных и максимальных значениях
в) максимальная дисперсия остатков при малых значениях 
и дисперсия остатков однородна по мере увеличения значений 
Для проверки выборки на гетероскедастичность можно использовать метод Гольдфельда-Квандта (при малом объеме выборки) или критерий Бартлетта (при большом объеме выборки).
Последовательность применения теста Гольдфельда-Квандта:
1) Упорядочить данные по убыванию той независимой переменной, относительно которой есть подозрение на гетероскедастичность.
2) Исключить из рассмотрения 
центральных наблюдений. При этом 
где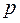 
– число оцениваемых параметров. Из экспериментальных расчетов для случая однофакторного уравнения регрессии рекомендовано при 
=30 принимать =8, а при =60 соответственно =16.
3) Разделить совокупность из 
наблюдений на две группы (соответственно с малыми и большими значениями фактора ) и определить по каждой из групп уравнение регрессии.
4) Вычислить остаточную сумму квадратов для первой 
и второй 
групп и найти их отношение 
где 
При выполнении нулевой гипотезы о гомоскедастичности отношение 
будет удовлетворять 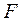-критерию Фишера со степенями свободы 
для каждой остаточной суммы квадратов. Чем больше величина превышает 
тем более нарушена предпосылка о равенстве дисперсий остаточных величин.
Если необходимо включить в модель факторы, имеющие два или более качественных уровней (пол, профессия, образование, климатические условия, принадлежность к определенному региону и т.д.), то им должны быть присвоены цифровые метки, т.е. качественные переменные преобразованы в количественные. Такого вида сконструированные переменные называют фиктивными (искусственными) переменными.
Коэффициент регрессии при фиктивной переменной интерпретируется как среднее изменение зависимой переменной при переходе от одной категории к другой при неизменных значениях остальных параметров. Значимость влияния фиктивной переменной проверяется с помощью -критерия Стьюдента.
2. Решение типовых задач
Пример 2.1. По 15 предприятиям отрасли (табл. 2.1) изучается зависимость затрат на выпуск продукции (тыс. ден. ед.) от объема произведенной продукции 
(тыс. ед.) и расходов на сырье 
(тыс. ден. ед). Необходимо:
1) Построить уравнение множественной линейной регрессии.
2) Вычислить и интерпретировать:
• средние коэффициенты эластичности;
• парные коэффициенты корреляции, оценить их значимость на уровне 0,05;
• частные коэффициенты корреляции;
• коэффициент множественной корреляции, множественный коэффициент детерминации, скорректированный коэффициент детерминации.
3) Оценить надежность построенного уравнения регрессии и целесообразность включения фактора после фактора и после 
Таблица 2.1
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| x1 | 2,7 | 1,5 | 8,2 | 4,5 | 3,3 | 5,8 | 3,0 | 7,1 |
| x2 | 55,7 | 52,0 | 120,1 | 80,3 | 29,8 | 110,5 | 90,4 | 118,2 |
| y |
| i | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
| x1 | 1,2 | 10,4 | 4,9 | 5,2 | 11,5 | 9,4 | 6,5 | |
| x2 | 24,7 | 298,9 | 58,2 | 120,3 | 224,7 | 271,2 | 102,0 | |
| y |
Решение:
1) В Excel составим вспомогательную таблицу 2.2.
Таблица 2.2
Аналогично примеру 1.1 вычислим: 
=345,5; 
=13838,89; 
=8515,78; 
=219,315; 
=9,37; 
=6558,08.
Затем найдем коэффициенты множественной линейной регрессии и оформим вывод результатов как на рис. 2.2.
Например, для вычисления значения коэффициента 
в ячейку F20 поместим формулу =(B20*B24-B21*B22)/(B23*B24-B22*B22) и получим 29,83. В ячейке F21 найдем 
=0,3 как =(B21*B23-B20*B22)/(B23*B24-B22*B22). Коэффициент =-13,02 вычислим по формуле =D18-B18*F20-C18*F21.
Уравнение множественной линейной регрессии примет вид:
=-13,02+29,83 
+0,3 
Таким образом, при увеличении объема произведенной продукции 
на 1 тыс. ед. затраты на выпуск этой продукции 
в среднем увеличатся на 29,83 тыс. ден. ед., а при увеличении расходов на сырье 
на 1 тыс. ден. ед. затраты увеличатся в среднем на 0,3 тыс. ден. ед.
Рис. 2.2. Решение примера 2.1 в Excel
2) Для вычисления средних коэффициентов эластичности воспользуемся формулой: Вычисляем: 
=0,88 и =0,18. Т.е. увеличение только объема произведенной продукции (от своего среднего значения) или только расходов на сырье на 1% увеличивает в среднем затраты на выпуск продукции на 0,88% или 0,18% соответственно. Таким образом, фактор оказывает большее влияние на результат, чем фактор 
Найдем значения парных коэффициентов корреляции:
=0,96; 
=0,89;
=0,88.
Значения парных коэффициентов корреляции указывают на весьма тесную связь с и на тесную связь с В то же время межфакторная связь 
очень сильная ( =0,88>0,7), что говорит о том, что один из факторов является неинформативным, т.е. в модель необходимо включать или 
или
Значимость парных коэффициентов корреляции оценим с помощью -критерия Стьюдента. =2,1604 определяем по таблице - критерия Стьюдента (таблица 2 приложения) взяв =0,05 и 
= -2=13 либо с помощью встроенной статистической функции СТЬЮДРАСПОБР с такими же параметрами.
Фактическое значение -критерия Стьюдента для каждого парного коэффициента определим по формулам: 
Получим 
=12,28; 
=7,19; 
=6,84.
Так как фактические значения -статистики превосходят табличные, то парные коэффициенты корреляции 
не случайно отличаются от нуля, а статистически значимы.
Вычислим частные коэффициенты корреляции по формулам:
Получим 
=0,38; 
=0,34; 
=0,21. Таким образом, фактор оказывает немного более сильное влияние на результат, чем
При сравнении значений коэффициентов парной и частной корреляции приходим к выводу, что из-за сильной межфакторной связи коэффициенты парной и частной корреляции отличаются довольно значительно.
Date: 2016-06-09; view: 13530; Нарушение авторских прав