Коэффициент детерминации

или

показывает долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака Соответственно, величина характеризует долю дисперсии показателя 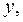вызванную влиянием неучтенных в модели факторов и прочих причин.

Чем ближе к 1, тем качественнее регрессионная модель, т.е. построенная модель хорошо аппроксимирует исходные данные.

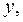Средняя ошибка аппроксимации – это среднее относительное отклонение теоретических значений от фактических т.е.

Построенное уравнение регрессии считается удовлетворительным, если значение не превышает 10-12%.

Для линейной регрессии средний коэффициент эластичности находится по формуле:

Средний коэффициент эластичности показывает на сколько процентов в среднем по совокупности изменится результат от своей величины при изменении фактора на 1% от своего значения.

Оценка значимости уравнения регрессии в целом дается с помощью 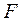-критерия Фишера, который заключается в проверке гипотезы о статис­ти­чес­кой незначимости уравнения регрессии. Для этого выполняется сравнение фактического и критического (табличного) значений 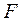- крите­рия Фишера.

определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы, т.е.

– максимально возможное значение критерия под влиянием случайных факторов при степенях свободы =1, = -2 и уровне значимости находится из таблицы 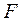-критерия Фишера (таблица 1 приложения).

Уровень значимости – это вероятность отвергнуть правильную гипотезу при условии, что она верна.

Если то гипотеза об отсутствии связи изучаемого показателя с фактором отклоняется и делается вывод о существенности этой связи с уровнем значимости (т.е. уравнение регрессии значимо).

Если то гипотеза принимается и признается статистическая незначимость и ненадежность уравнения регрессии.

Для линейной регрессии значимость коэффициентов регрессии оценивают с помощью - критерия Стьюдента, согласно которому выдвигается гипотеза о случайной природе показателей, т.е. о незначимом их отличии от нуля. Далее рассчитываются фактические значения критерия для каждого из оцениваемых коэффициентов регрессии, т.е.

где и – стандартные ошибки параметров линейной регрессии определяются по формулам:

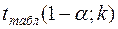– максимально возможное значение критерия Стьюдента под влиянием случайных факторов при данной степени свободы = -2 и уровне значимости находится из таблицы критерия Стьюдента (таблица 2 приложения).

Если то гипотеза о несущественности коэффициента регрессии отклоняется с уровнем значимости т.е. коэффициент ( или )не случайно отличается от нуля и сформировался под влиянием систематически действующего фактора

Если то гипотеза не отклоняется и признается случайная природа формирования параметра.

Значимость линейного коэффициента корреляции также проверяется с помощью - критерия Стьюдента, т.е.

Гипотеза о несущественности коэффициента корреляции отклоняется с уровнем значимости если

Замечание. Для линейной парной регрессии проверки гипотез о значимости коэффициента и коэффициента корреляции равносильны проверке гипотезы о существенности уравнения регрессии в целом, т.е.

Для расчета доверительного интервала определяют предельную ошибку для каждого показателя, т.е.

Доверительные интервалы для коэффициентов линейной регрессии:

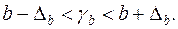
Если в границы доверительного интервала попадает ноль, т.е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимается нулевым, т.к. он не может одновременно принимать и положительное, и отрицательное значения.

Date: 2016-06-09; view: 1003; Нарушение авторских прав