Переходная матрица и матрица импульсных переходных функций линейной системы

Определения линейной динамической системы, приведенные в предыдущем параграфе, устанавливают принципиальную основу исследования линейных систем.

Для получения ряда конструктивных результатов необходимо иметь такую характеристику системы, которая бы однозначно ей соответствовала и наиболее полно раскрывала свойства системы. К получению этой характеристики мы и приступим.

Рассмотрим дифференциальное уравнение линейной системы

(5.33)

полученное из уравнения состояния системы

, (5.34)

путем приравнивания нулю вектора входных воздействий U (t).

Уравнение (5.33) будет описывать движение системы, возникающее только из-за начальных отклонений, которые определяются вектором начальных условий Х(t ) в момент t=t . Введем для этого вектора специальное обозначение

. (5.35)

Всякий вектор Х(t), удовлетворяющий уравнению (5.33) при любом заданном векторе начальных условий Λ, называется решениемуравнения Х(t)=Х(t,Λ), причем для t = t должнобыть Х (t, Λ ) = Λ.

Обычно рассмотрение уравнений (5.34) и (5.35) начинается с доказательства теорем существования и единственности решения. Поскольку основной задачей дальнейшего рассмотрения является, главным образом, изучение свойств решения, мы ограничимся лишь формулировкой основной теоремы без доказательства.

Если матрица F (t) непрерывна по t, для каждых значений t и t = Т и начальных условий Λ, < , существует единственное решение уравнения(5.33) Х(t₀, Λ ).

Таким образом, для определенного значения t существует множество векторов (функций) Х(t ,Λ), зависящих от вектора начальных условий Λ. Это множество образует линейное пространство решений, так как в соответствии с определением 5.6 пространство состояний системы является линейным (векторным).

Теперь возникает вопрос, какова размерность этого пространствами? Покажем, что пространство решений Х(t, Λ ) уравнения (5.33) является n-мерным, где n - числострок матрицы F(t).

Поскольку вектор Λначальных условий является произвольным, выберем в линейном пространстве n линейно независимых постоянных векторов , каждый из которых является начальным вектором уравнения (5.33) и входит в числовое пространство R , так как начальные условия являются числами.

Эти векторы образуют базис n-мерного линейного пространства R . Таким образом, любой вектор начальных условий может быть разложен по этому базису:

где - координаты разложения.

В соответствии с теоремой о существовании и единственности решения для каждого вектора начальных условий, в пространстве решений всегда найдется n однозначно определенных решений Х (t,λ ) для п различных начальных условий λ уравнения (5.33), причем

.

Составим из них линейную комбинацию

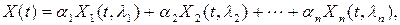(5.36)

которая также будет решением уравнения (5.33).

Покажем, что эта комбинация линейно независима. Предположим обратное. Тогда, при некоторых , отличных от нуля, функция Х(t) по крайней мере при одном произвольном значении t=τ будет равна нулю:

Но в силу теоремы о единственном решении при заданных λ ; функция Х(τ) должна быть равна нулю для всех следовательно, и для . При этом мы получим (учитывая, что Х (t,λ )=λ )

.

Однако, это противоречит условию линейной независимости векторов λ следовательно, комбинация (5.36) является линейно независимой.

Так как координаты разложения (5.36) взяты теми же, что и в разложении (5.35), то при t=t получим

.

Следовательно, Х (t) действительно является решением при любом векторе начальных условий Λ. Таким образом, функции Х_i(t₀,λ ), i=1,2,...,n, являются линейно независимыми векторами в n-мерном пространстве и образуют его базис.

Рассмотрим понятие фундаментальной матрицы решений. Для большей наглядности проведем необходимые рассуждения на примере системы уравнений 2-го порядка.

Введем в рассмотрение матрицу

, (5.37)

и матрицу-столбец

, (5.38)

получим уравнение (5.33) в следующем развернутом виде (для простоты записи аргумент t опустим):

(5.39)

Если задать пару начальных условий в виде , то уравнениям (5.39) должны удовлетворять некоторые частные решения x (t, x ,0), x (t, x ,0), которые обозначим γ (t,t ) и γ (t, t ). Первый индекс у этих решений обозначает номер функции х (t) в уравнениях (5.39), а второй - номер отличного от нуля начального условия.

Меняя теперь местами значения начальных условий, т. е. задавая x (t ) = 0, x (t )=x , аналогично предыдущему запишем соответствующие частные решения в виде γ (t, t ) и γ (t, t ). Очевидно, функции γ_ij (t, t ) являются составляющими соответствующих векторов-решений, а значения начальных условий - составляющими начальных векторов:

(5.40)

При t=t мы должны получить Х (t , )= , Х (t , )= . Обобщая эти соотношения на уравнения n-го порядка, можем записать

, (5.41)

где первый индекс у функции γ обозначает номер строки матрицы F(t), а второй - номер начального вектора .

Положим в нашем примере системы 2-ro порядка начальные условия единичными, т. е. х =1, х = 1. Соответствующие частные решения обозначим через . Тогда будут иметь место соотношения

или, в матричной форме,

Обобщая эти соотношения на уравнения n - го порядка, можем записать:

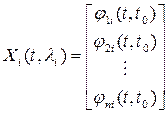, (5.42)

и при t=t Х (t, λ ) = λ , так как

. (5.43)

Вернемся к уравнениям (5.39). Полученные частные решения (5.40) приводят при их подстановке в уравнения (5.39) к следующим тождествам:

Эти соотношения можно записать в виде элементов матриц

(5.44)

где каждый элемент правой матрицы равен соответствующему элементу левой матрицы. Применяя формулу умножения двух матриц, можно установить, что правая матрица является произведением двух матриц

(5.45)

Введем обозначение

,

и, используя выражение (5.37), запишем соотношение (5.44) в виде

(5.46)

Для системы n-го порядка матрица Г(t, t )будет иметь вид

. (5.47)

Матрица Г(t, t ) называется фундаментальной матрицей решений. Столбцы этой матрицы линейно независимы, следовательно, определитель матрицы отличен от нуля. В самом деле, используя формулу (5.41), матрицу (5.47) можно записать в виде

где функции (векторы) Х (t, λ ), играющие здесь роль столбцов, линейно независимы. Подставляя в последнее выражение значения Х (t,λ ), определяемые формулой (5.42), получим:

Введем обозначения

(5.48)

Тогда

Матрица Ф(t, t ) называется переходной матрицей сucmeмы. Смысл этого наименования установим ниже.

Заметим, что вектор Λ -это начальный вектор, построенный на составляющих λ с координатами разложения α равными единице. Если все составляющие начального вектора Λ сделать единичными, λ =λ =...=λ =1, то фундаментальная матрица решений совпадет с переходной матрицей. Последняя, при t=t становится единичной, так как имеют местозначения φ определяемые (5.43):

(5.49)

На основании соотношения (5.46) можно заключить, что переходная матрица удовлетворяет уравнению

(5.50)

Сравнивая это выражение с уравнением (5.33), видим, что Ф (t, t ) можно трактовать как вектор в n-мерном пространстве с линейно независимыми составляющими в виде строк матрицы (5.48).

Введение понятия переходной матрицы позволяет поставить задачу отыскания непосредственной связи между вектором состояний системы и вектором входных воздействий.

Будем искать решение уравнения (5.34) в виде

(5.51)

где K(t, t ) - некоторая матрица, зависящая от вектора входного сигнала U(t).

Дифференцируя соотношение (5.51) по времени, получим

.

Подставляя значения Х(t) из (5.51) и полученное выражение для dХ/dt в уравнение (5.34), будем иметь

или

(5.52)

так как на основании (5.50) имеет место тождество

Поскольку столбцы переходной матрицы Ф(t,t ) линейно независимы, матрица является невырожденной и имеет обратную матрицу Ф (t,t ). Умножая соотношение (5.52) слева на Ф^-1(t,t ) и учитывая свойство обратной матрицы

Ф^-1(t,t ) Ф(t, t )=I,

получим

Интегрируя это выражение в пределах от t до t будем иметь

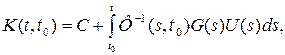
причем, когда t=t₀, С = K(t₀, t₀), Умножая соотношение (5.51) слева на Ф^-1 положив затем t=t и учитывая на основании (5.49), что Ф^-1 = I, получим С = Х(t ).

Подставляя значения K(t, t₀), и С в формулу (5.51), окончательно будем иметь:

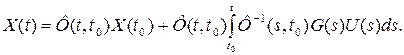(5.53)

Формула (5.53) устанавливает связь между вектором состояния системы Х (t), вектором начальных условий. Х(t₀)и вектором входных воздействий U(t)через переходную матрицу системы Ф(t, t₀). Таким образом, переходнаяматрица является характеристикой линейной системы, полностью определяющей ее динамические свойства. Если входное воздействие отсутствует, U(t)=0, вектор состояния системы определяет так называемое свободное движение системы. На основании формулы (5.53) он будет равен

Х(t) = Ф(t, t₀)Х(t₀), U(t)=0. (5.54)

Полученное соотношение показывает, что матрица Ф(t,t₀) определяет переход системы из начального состояния в момент t₀, в состояние Х(t), соответствующее моменту времени t. По этой причине Ф (t,t₀) и называется переходной матрицей системы.

Если до подачи входного воздействия система находилась в покое Х(t₀)=0, вектор состояния системы после подачи входного воздействия будет определять вынужденное движение. При этом формула (5.53) примет вид

Установим теперь некоторые свойства переходной матрицы.

Используя формулу (5.54), можем записать

откуда

С другой стороны, имеем

следовательно,

(5.55)

Полученная формула является конкретной реализацией полугруппового свойства переходной функции состояний, данного в общем определении 5.1.

Положив в формуле (5.55) получим

откуда

(5.56)

Формулы (5.55) и (5.56) можно применить для преобразования соотношения (5.53) к более удобной форме. Заменим в нем обратную матрицу по формуле (5.56) на , введем под знак интеграла матрицу так как она не зависит от переменной интегрирования s, и заменим полученное произведение по формуле (5.55) на . Окончательно получим

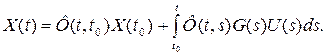(5.57)

Эта формула более удобна для расчетов, чем (5.53), так как не содержит обратной матрицы.

Рассмотрим линейную систему, состояние которой для моментов времени характеризуется нулевым начальным вектором . В момент 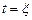на систему подается входное воздействие

, (5.58)

где N матрица-столбец чисел

. (5.59)

Рассматриваемое входное воздействие представляет собой набор импульсных входных сигналов в виде дельта - функций с «площадями» n₁, n₂,…, n_m. Последние определяются как предел выражения

где - любая непрерывная четная функция с параметром αтакая, что при будет Сама дельта-функция определяется соотношениями

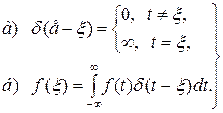(5.60)

Подставим в формулу (5.57) выражение (5.58) и положим . Будем иметь

.

Интегрирование матрицы есть интегрирование каждого из ее элементов. Поэтому к полученному выражению применима формула (5.60), определяющая основное свойство дельта-функции. В результате получим

. (5.61)

Положим теперь «площади» всех действующих на входе дельта-функций равными единице. При этом

.

Получаемое при таком воздействии множество выходных сигналов есть не что иное, как множество импульсных переходных функций. Поэтому получаемой матрице целесообразно дать специальное обозначение и наименование матрицы импульсных переходных функций

. (5.62)

Так как матрица - квадратная (содержит nстрок и n столбцов), а матрица имеет n строк и т столбцов, их произведение будет иметь и строк и т столбцов. Запишем матрицу в развернутом виде

, (5.63)

где функции являются реакцией i -го выхода системы на j -й вход (рисунок 5.9). Тогда, очевидно, реакция i -го выхода на все т входов будет равна сумме элементов i -й строки матрицы (5.63). Формулу (5.61) с учетом соотношения (5.62) можно записать в виде

или, заменяя на

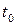
. (5.64)

Сравнивая эту формулу с соотношением (5.54) для определения вектора состояний при свободном движении системы, видим, что матрица импульсных переходных функций отображает вектор «энергий» дельта-функций в текущее состояние системы. Это обстоятельство позволяет осуществить пересчет вектора начальных условий в эквивалентный вектор входных сигналов . Тем самым во всех случаях вектор состояний системы можно определять как результат входных воздействий на систему, находившуюся до этого в покое. При этом формула (5.57) может быть заменена следующей формулой, с учетом соотношения (5.62):

(5.65)

где

. (5.66)

Подставляя (5.66) в формулу (5.65), легко убедиться в справедливости такой замены.

Для определения значений матрицы-столбца N, соответствующих значениям вектора начальных условий , воспользуемся выражениями (5.62) (заменив на 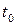) и (5.54):

Приравнивая правые части этих соотношений и определяя N, получим

. (5.67)

Контрольные вопросы

1) Какая система называется динамической?

2) Как определяется переходная характеристика линейной системы?

3) Как определяется импульсная переходная характеристика линейной системы?

4) Какая матрица называется фундаментальной матрицей решений?

Date: 2016-02-19; view: 579; Нарушение авторских прав