
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

ТЕМА 12. Страховая статистика
|
|
Требования к знаниям: знать экономическую сущность страхования, функции страхования, виды страхования.
Значимость страхования в период развития рыночных отношений. Понятие страхового фонда. Экономическая категория страхования. Личное, имущественное страхование. Риск и страхование.
4.Вопросы к экзаменам по дисциплине «Статистика».
1. Предмет и основные категории статистики.
2. Методы и задачи статистики.
3. Органы государственной статистики РФ.
4. Функции и права Росстата РФ.
5. Основные этапы статистического исследования.
6. Статистическое наблюдение – первый этап статистического исследования.
7. Формы, виды и способы наблюдения.
8. Понятие о выборочном наблюдении.
9. Ошибки выборочного наблюдения, их виды.
10. Сводка статистических данных.
11. Группировка статистических данных.
12. Статистические таблицы, их значение. Виды статистических таблиц.
13. Статистические графики, их основные элементы.
14. Абсолютные величины, их виды. Значение абсолютных величин.
15. Относительные величины, их сущность. Формы выражения и виды.
16. Сущность и виды средних величин.
17. Сущность моды и медианы.
18. Показатели вариации. Среднее квадратическое отклонение: простое и взвешенное.
19. Ряды динамики. Понятие и виды рядов динамики.
20. Показатели ряда динамики и методы их расчета.
21. Виды рядов распределения. Его элементы: варианты признака, частоты или веса.
22. Понятие об индексах и методы их расчета.
23. Агрегатные индексы физического объема товарооборота, цен, товарооборота в физических ценах. Взаимосвязь индексов.
24. Средний арифметический индекс физического объема товарооборота и средний гармонический индекс цен.
25. Статистика продукции. Издержки производства и обращения.
26. Система показателей демографической статистики.
27. Изучение миграции населения. Перспективные расчеты численности населения.
28. Занятость и безработица, трудовые ресурсы. Показатели движения рабочей силы.
29. Экономическая категория страхования.
5.Общие методические указания по выполнению и оформлению
контрольной работы.
Согласно учебному плану студенты-заочники должны выполнить одну домашнюю контрольную работу. Задание для контрольной работы составлено в 10 вариантах. Каждый вариант предусматривает письменный ответ на один вопрос и решение 4 задач. Студент должен выполнить тот вариант, который соответствует последней цифре номера его личного дела. Например, студенты, имеющие номера личных дел 108, 218, 1438, выполняют контрольную работу по варианту №8, имеющие номера личных дел 90, 700, 1010, - по варианту №10 и т.д..
Контрольная работа должна быть выполнена четко и аккуратно в тетради с полями для замечаний рецензента.
На первой странице студенту необходимо написать название предмета, номер варианта и личного дела, фамилию и инициалы.
К выполнению контрольной работы студент должен подходить творчески, максимально используя свой производственны опыт, изучив рекомендуемую литературу.
В конце работы следует указать использованную литературу. Зачтенные контрольные работы представляются на экзамене.
Если студенты затрудняются в решении какой-либо задачи, они могут обратиться письменно или устно к преподавателю статистики колледжа.
Изучение дисциплины «Статистка» возможно, используя специальную литературу, учебные пособия, а так же лекции преподавателя.
Тема 1. Статистические наблюдения.
Любое статистическое исследование, любое познание общественной жизни начинается со сбора сведений об изучаемых явлениях и процессах. Научно-организационная работа по сбору статистической информации о явлениях и процессах общественной жизни называется статистическим наблюдением. Статистическое наблюдение имеет программу и организационный план и проводится с соблюдением ряда требований, важнейшими из которых являются достоверность и полнота информации.
Статистический материал, собранный в результате статистического наблюдения, должен быть точным, достоверным. Поэтому первичный материал перед его обработкой подвергается предварительному контролю, который может быть логическим и арифметическим (счетным).
Задача. Имеются следующие данные из Формы №3 – торг «Отчет о поступлении, продаже и остатках товаров» торговой организации за квартал (тыс.руб.):
Таблица 1.1.
| № | Наименование товарных групп | Остатки товаров на начало квартала | Поступило товаров за квартал | Передано в общественное питание и прочий документированный расход, не являющийся розничной продажей | Продано в розницу и прочий недокументированный расход (гр.1+гр.2 –гр.3-гр.5) | Остатки товаров на конец квартала |
| А | ||||||
| 1. 2. 3. 4. | Мясо Масло животное Сахар Кондитерские изделия | |||||
| Итого |
Требуется проверить правильность исчисления данных гр.4 и итоговых показателей. Следует иметь в виду, что движение товаров в торговом предприятии можно представить в балансовой форме, которая имеет вид следующего уравнения:
остаток на поступление расход остаток на
начало периода + за период = за период + конец периода
(гр.1+гр.2 = гр.3+гр.4+гр.5. Отсюда гр.4 = гр.1+гр.2-гр.3-гр.5)
При контроле можно применить логическую и арифметическую проверки.
Начинаем проверку с первой товарной группы – мясо. Считаем остатки, поступление и продажу. Наблюдаются незначительные расхождения. Далее проверяем арифметически: 32+270=60+212+30, т.е. 302=302. Имеется балансовое равенство. Проверяем (гр.4) «продано в розницу»: 32+270-60-30=212. Ответы увязываются логически и арифметически. По товарной группе – масло животное – обращает на себя внимание в гр.4 цифра 900. Проверяем, есть ли балансовая увязка: 20+90=5+900+20. Равенства нет.
Исходя из взаимосвязи покупателей исчисляем данные гр.4. Получили 90 (20+95-5-20=90). Теперь проверяем балансовое равенство: 20+95=5+90+20, т.е. 115=115. Оно имеется. Значит, допущена ошибка. Видимо, при заполнении отчета механически вместо цифры 90 записана цифра 900, т.е. подставлен лишний нуль. Вносим исправление: в гр.4, стр.2 вместо 900 ставим 90.
Аналогично проверяем каждую строку отчета по товарной группе. По товарной группе – сахар – не получается балансовой увязки (35+215=13+213+32). Проверяем расчет гр.4: 35+215-13-32=205. В отчете написано 213, значит, допущена арифметическая ошибка. Вносим исправления: вместо 213 записываем 205.
По кондитерским изделиям балансовая увязка получается 55+210=8+197+60, т.е. 265=265. Ошибки нет. Далее проверяем итоговые показатели отчета, суммируя данные по каждой графе отдельно, и затем увязываем балансовой равенство. Итоги по гр.1, 2, 3, 5 подсчитаны правильно. По гр.4 с учетом внесенных исправлений получаем 704 (212+90+205+197) и записываем вместо 712. теперь итоговые данные соответствуют балансовой схеме: 142+790=86+704+142, т.е. 932=932.
Отчет проверен, исправления внесены, данные можно использовать для оперативной и аналитической работы.
Изученный материал по данной теме следует использовать при решении задач №1 вариантов №1, 4.
Тема 2. Сводка и группировка статистических данных.
В результате первой стадии статистического исследования – статистического наблюдения – получают сведения о каждой единице совокупности. Задача второй стадии статистического исследования состоит в том, чтобы упорядочить и обобщить первичный материал, свести его в группы и на этой основе дать обобщенную характеристику совокупности. Этот этап в статистике называется сводкой.
Различают простую сводку (подсчет только общих итогов) и статистическую группировку, которая сводится к расчленению совокупности на группы по существенному для единиц совокупности признаку. Группировка позволяет получить такие результаты, по которым можно выявить состав совокупности, характерные черты и свойства обычных явлений, обнаружить закономерности и взаимосвязи.
Результаты сводки могут быть представлены в виде статистических рядов распределения.
Статистическим рядом распределения называют упорядоченное распределение единиц совокупности на группы по изучаемому признаку. В зависимости от признака ряды могут быть вариационные (количественные) и атрибутивные (качественные). Количественные признаки – это признаки, имеющие количественное выражение у отдельных единиц совокупности, например заработная плата рабочих, стоимость продукции промышленных предприятий, возраст людей, урожайность отдельных участков посевной площади и т.д.
Атрибутивные признаки – это признаки, не имеющие количественной меры. Например, пол (мужской, женский), отрасль народного хозяйства, вид продукции, профессия рабочего и т.д.. Вариационные ряды могут быть дискретными или интервальными.
Дискретный ряд распределения – это ряд, в котором варианты выражены целым числом. Примером может служить распределение рабочих по тарифным разрядам.
Задача. Имеются следующие данные о работе 24 заводов одной из отраслей промышленности.
Таблица 2.1.
| № | Среднегодовая стоимость основных производственных фондов, млн.р. | Среднесписочное число работающих за отчетный период, чел. | Производство продукции за отчетный период, млн.р. | Выполнение плана, % |
| 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. | 3,0 7,0 2,0 3,9 3,3 2,8 6,5 6,6 2,0 4,7 2,7 3,3 3,0 3,1 3,1 3,5 3,1 5,6 3,5 4,0 1,0 7,0 4,5 4,9 | 3,2 9,6 1,5 4,2 6,4 2,8 9,4 11,9 2,5 3,5 2,3 1,3 1,4 3,0 2,5 7,9 3,6 8,0 2,5 2,8 1,6 12,9 5,6 4,4 | 103,1 120,0 109,5 104,5 104,8 94,3 108,1 125,0 101,4 102,4 108,5 102,1 112,7 92,0 108,0 111,1 96,9 114,1 108,0 107,0 100,7 118,0 111,9 104,7 | |
| 94,1 | 114,8 |
Если по каждому абсолютному показателю таблицы подвести итоги, то получим простую сводку. Однако только по итогам и отдельным показателям трудно судить о характере распределения заводов, например по проценту выполнения плана, по числу работающих или по стоимости основных фондов, о том, какие значения показателей являются наиболее характерными для данной отрасли за отчетный год. Для этого имеющиеся данные надо привести в систему по интересующему нас признаку. В качестве изучаемого признака возьмем, например, стоимость основных фондов и построим по нему ряд распределения с равными закрытыми интервалами. Величина интервала в этом случае определяется по формуле

где xmax и xmin - соответственно максимальное и минимальное значения стоимости основных фондов.
Образуем пять групп заводов. Тогда величина интервала будет равна:

Теперь образуем группы заводов, отличающихся друг от друга по среднегодовой стоимости основных производственных фондов на эту величину. Первая группа заводов будет иметь размер основных производственных фондов в пределах от 1 до 2,2 млн.руб., вторая группа определится в пределах границ от 2,2 до 3,4 и т.д.. Распределив заводы по группам, подсчитаем число заводов в каждой из них.
Техника подсчета проста. Можно сделать выборку нужных значений из таблицы 2.1 и занести их предварительно в рабочую таблицу:
Группы заводов по стоимости основных Число заводов
производственных фондов, млн.руб.
1,0 – 2,2  ׀׀׀
׀׀׀
 2,2 – 3,4 ׀׀׀׀ ׀׀׀׀
2,2 – 3,4 ׀׀׀׀ ׀׀׀׀
 3,4 – 4,6 ׀׀׀׀
3,4 – 4,6 ׀׀׀׀
4,6 – 5,8 ׀׀׀
5,8 – 7,0 ׀׀׀׀
Примечание. Каждая черта соответствует единице совокупности, т.е. по одному заводу. Счет ведется пятерками – каждые черты перечеркиваются пятой.
На основании рабочей таблицы составляется ряд распределения заводов по размеру основных фондов:
Таблица 2.2.
| Группы заводов по стоимости основных производственных фондов, млн.руб. | Число заводов | Удельный вес заводов группы в процентах к итогу |
| 1,0 – 2,2 2,2 – 3,4 3,4 – 4,6 4,6 – 5,8 5,8 – 7,0 | 12,5 37,5 20,8 12,5 16,7 | |
| Итого | 100,0 |
Этот способ подсчета водится к следующему. Предварительно составляется ранжированный ряд распределения, т.е. ряд, в котором значение признака располагается в возрастающем или убывающем порядке и счет ведется по группам.
Построим ранжированный ряд заводов по стоимости основных производственных фондов в возрастающем порядке.
Таблица 2.3.
| Номер группы | Номер завода по порядку | Стоимость основных производственных фондов, млн.руб. | Номер группы | Номер завода по порядку | Стоимость основных производственных фондов, млн.руб. | |
| 1. | 1,0 2,0 2,0 | 3. | 3,5 3,5 3,9 4,0 4,5 | |||
| 2. | 2,7 2,8 3,0 3,0 3,1 3,1 3,1 3,3 3,3 | |||||
| 4. | 4,7 4,9 5,6 | |||||
| 5. | 6,5 6,6 7,0 7,0 |
По данным ранжированного ряда хорошо видно изменение стоимости основных производственных фондов и легко обозначить границы групп. В группу заводов с размером стоимости основных фондов 1 – 2,2 войдут первые по порядку три завода, во вторую группу 2,2 – 3,4 войдут следующие по порядку девять заводов и т.д.. Составив предварительно макет таблицы и заполнив его получим табл. 2.3, аналогичную табл. 2.2..
Как видно из табл. 2.2, ряд распределения состоит из двух элементов: 1) значение признака; 2) абсолютной численности единиц признака.
Для большей наглядности абсолютные величины могут быть дополнены относительными показателями (частностями), выраженными в процентах. Таким образом, обобщение данных в виде ряда распределения позволяет видеть вариацию и состав совокупности по изучаемому признаку, сравнивать между собой группы, изучать их в динамике. Итак, ряд распределения заводов по стоимости основных производственных фондов показывает, что для данной отрасли характерной является группа заводов с основными фондами от 2,2 до 3,4 млн.руб., которая составляет 37,5% всех заводов, и что более половины заводов (58,3%) имеют стоимость основных фондов в размере от 2,2 до 4,6 млн.руб.
Интервалы в рядах распределения могут быть неравными - прогрессивно возрастающими или прогрессивно убывающими. Это характерно для совокупностей с большими колебаниями значений признака.
Примером может служить следующий ряд распределения:
Таблица 2.4.
| Группа заводов по объему продукции, млн. руб. | Число заводов | Удельный вес заводов в процентах к итогу |
| До 100 100 – 200 200 – 400 400 – 700 Свыше 1000 | 6,7 10,0 16,7 13,3 20,0 33,3 | |
| 100,0 |
Этот ряд имеет так же открытые интервалы в первой и последней группах.
Рассмотрим ряды распределения по атрибутивному признаку.
Задача. По данным табл. 2.1 произведем группировку по атрибутивному признаку, выделив две группы заводов: не выполнивших план и выполнивший план.
Подсчитав число заводов по группам и, оформив результаты в виде таблицы, получим следующий ряд распределения заводов по результатам производственной деятельности.
Таблица 2.5.
| Группы заводов | Число заводов | Удельный вес заводов в % к итогу |
| Не выполнившие план Выполнившие план | 12,5 87,5 | |
| 100,0 |
Табл. 2.5. дает наглядное представление о составе совокупности и характеризует производственную деятельность отрасли.
Другим примером атрибутивного ряда распределения служит табл. 2.6., характеризующая распределение среднегодовой численности рабочих и служащих по отраслям хозяйствования в текущем году.
Таблица 2.6.
| Численность рабочих и служащих, тыс. чел. | Удельный вес в процентах к итогу | |
| Всего по отраслям в том числе: промышленность (промышленно-производственный персонал) сельское и лесное хозяйство транспорт и связь строительство торговля, общественное питание, материально-техническое снабжение и сбыт, заготовки жилищно-коммунальное хозяйство и бытовое обслуживание населения прочие отрасли народного хозяйства (здравоохранение, народное образование, культура, аппарат органов управления и т.д.) | 33,2 10,8 10,6 10,2 8,6 3,9 22,7 |
Таблица дает наглядное представление о распределении рабочих и служащих по отраслям.
Изученный материал по данной теме следует использовать при решении задач №1 вариантов № 2, 5, 8, 10 и №2 варианта №1.
Тема 3. Способы наглядного представления статистических данных.
Статистические таблицы.
Составление статистических таблиц – большое искусство, овладеть которым помогают практические упражнения, основанные на знании теоретического материала. Важным моментом является составление макета таблицы.
Макетом таблицы называется таблица, состоящая из строк и граф, которые еще не заполнены цифрами. Каждая статистическая таблица (макет) имеет подлежащее и сказуемое. Подлежащее таблицы – это объект нашего изучения. Сказуемое – это система показателей, которыми характеризуется объект изучения, т.е. подлежащее таблицы. Обычно подлежащее располагается слева, в виде наименования горизонтальных строк, а сказуемое – справа, в виде наименования вертикальных граф.
В зависимости от построения подлежащего различают следующие виды таблиц: простые, групповые, комбинационные. Простыми таблицами называют такие, в подлежащем которых нет группировок, а дается лишь перечень единиц совокупности (перечневые таблицы), административных районов (территориальные таблицы) или периодов времени (хронологические таблицы).
Например: Котировка облигаций сберегательного займа в одном из межбанковских объединений на определенную дату.
(млн. руб.)
| Облигации по номерам серии | Объем покупки | Объем продажи |
| 122,5 112,6 123,2 124,4 | 123,4 113,5 124,4 108,35 | |
| Всего | 482,7 | 469,65 |
В данной таблице подлежащее – облигации государственного внутреннего займа. Это простая перечневая таблица.
Групповая таблица.
Распределение несовершеннолетних, совершивших правонарушения и преступления в течение года (по возрасту).
(тыс. чел.)
| № группы | Группы несовершеннолетних по возрасту | Всего | В том числе | ||
| Имели привод в милицию | Состоят в милиции на учете | Совершили преступления | |||
| До 13 лет 14 -15 16 -17 | 250,2 401,2 584,5 | 168,6 206,2 281,5 | 81,6 128,1 166,1 | 66,9 136,9 | |
| Итого | 1235,9 | 656,3 | 375,8 | 203,8 |
Подлежащее – группы несовершеннолетних, совершивших правонарушения и преступления по возрасту.
Комбинационная таблица.
Группировка рабочих цеха по стажу и квалификации.
| Группы рабочих по стажу | Число рабочих | В том числе по квалификации | |||||
| До 3-х лет От 3 до 5 лет От 5 до 10 лет От 10 до 25 лет От 25 лет и выше | |||||||
| итого |
Подлежащее – группы рабочих по стажу и квалификации.
Изученный материал по данной теме следует использовать при решении задач №1 вариантов 3, 7, 8, 9 и №2 варианта №5.
Тема 4. Абсолютные и относительные величины.
По данной теме предусматривается решение следующих типов задач:
1. определение относительных величин выполнения плана;
2. определение относительных величин плана;
3. определение относительных величин динамики;
4. определение относительных величин сравнения;
5. определение относительных величин интенсивности.
Относительные величины выполнения плана дают количественную характеристику выполнения плановых заданий. Способы вычисления относительных величин выполнения плана зависят от характера показателей, выражающих плановой задание. Так, для экономических явлений, которым свойственно поступательное развитие во времени, плановыми заведениями обычно устанавливается достижение в предстоящих периодах тех или иных абсолютных (или средних) уровней. Относительные величины выполнения плана определяются для них как процентное отношение фактически достигнутой в отчетном периоде абсолютной величины уровня к абсолютной величине уровня планового задания:

Задача. Имеются следующие данные о производстве в отчетном периоде продукции промышленными предприятиями города:
Таблица 4.1.
| Предприятия отрасли | По плану, млн.руб. | Фактически, млн.руб. | Процент выполнения плана |
| Машиностроения и металлообработки Текстильной промышленности Пищевой промышленности | 63,0 18,0 21,5 | 66,4 17,6 22,1 | 105,4 97,8 102,7 |
| Итого | 102,5 | 106,1 | 103,5 |
В последней графе определены относительные величины выполнения плана продукции в отчетном периоде по отраслям производства и по промышленности города в целом.
Для наглядного представления итогов выполнения промышленностью города плана производства продукции полученные данные целесообразно нанести на полосовой график (рис. 4.1.).
Для некоторых явлений задания плана предусматривают не рост, а снижение уровней на ту или иную величину. Относительные величины выполнения плана в таких случаях определяются путем сравнения фактически достигнутого и запланированного снижения уровня:


Рис. 4.1. Выполнение плана производства продукции промышленности предприятиями города (в %); 1-машиностроение металлообработка; 2-текстильная промышленность; 3-пищевая промышленность; 4-вся промышленность.
Задача. Планом на 2006 год намечено снижение себестоимости изделия А на 1,5 руб. при уровне себестоимости этого изделия 75,0 руб.. Фактически в 2006 году себестоимость этого изделия составила 73,44 руб.. Определите относительную величину выполнения плана по снижению себестоимости изделия А в 2006 году.
Для исчисления процента выполнения плана по снижению в 2006 году себестоимости изделия А найдем фактическую величину снижения себестоимости:
75,0 – 73,44=1,56 (руб.).
Рассчитаем относительную величину выполнения плана как отношение величины фактического снижения себестоимости (1,56) к величине снижения себестоимости по плановому заданию:

Таким образом, плановое задание по снижению себестоимости изделия А в 2006 году перевыполнено на 4,0%.
В экономическом анализе плановое задание может быть выражено и в форме относительной величины, т.е. в виде коэффициента роста или прироста уровня в планируемом периоде по сравнению с уровнем базисного периода. В этом случае относительная величина выполнения плана определяется из процентного сопоставления коэффициента фактического роста явления с плановым коэффициентом:

Задача. Прирост выпуска продукции отрасли по плану на 2006г. должен составить 7,5%. Фактически рост выпуска продукции в этом году составил 109,5%. Определите относительную величину выполнения плена отраслью по выпуску продукции.
Заданный планом прост выпуска продукции (7,5%) выражением в форме коэффициента роста выпуска продукции в 2006 году по сравнению с 2005годом: 1+0,075=1,075.
Фактический процент роста выпуска продукции (109,5%) выражением в форме коэффициента:  .
.
С помощью полученных коэффициентов рассчитываем относительную величину выполнения плана:  ,
,
т.е. в 2006 году план выпуска продукции перевыполнен отраслью на 1,9%.
Относительные величины структуры характеризуют долю (удельный вес) составных частей целого в их общем итоге и обычно выражаются в виде коэффициентов (доли единиц) или процентах. Важное значение относительных величин структуры в экономической статистике состоит в том, что они применяются для изучения состава (строения)статистической совокупности. Сопоставление структуры явлений, существующих в пространстве, позволяет выявить особенности их внутреннего строения. Сравнение же структуры явления, развивающегося во времен, позволяет изучать происходящее в явлении структурные сдвиги (изменения).
При определении относительных величин структуры сравниваемыми величинами могут быть или численности отдельных групп статистической совокупности, или объемы их признаков. За основание (базу) сравнения принимается общий итог статистической совокупности.
Задача. Имеются следующие данные о составе посевных площадей в колхозах и совхозах области о состоянию на 1 ноября 2006 года (тыс. га).
Таблица 4.2.
| Вид культуры | Посевная площадь | |
| В колхозах | В совхозах | |
| Зерновые Технические Картофель и овощебахчевые Кормовые | 570,6 105,6 27,9 299,0 | 595,9 34,6 17,8 276,8 |
| Итого | 1003,1 | 925,1 |
Для изучения использования посевных площадей колхозами и совхозами области определите относительные величины структуры и изобразите их графически.
Для расчета относительных величин структуры сопоставим посевные площади, занятые под отдельными культурами fi, с общим итогом ∑f, т.е. определим их удельный вес в процентах  .
.
Зерновые культуры:
в колхозах в совнархозах

 .
.
Технические культуры:
в колхозах в совнархозах

 .
.
Аналогично исчисляются показатели по остальным видам культур.
В результате расчетов получаем следующие данные о структуре посевных площадей в колхозах и совхозах области на 1 ноября 1998 года (%):
Таблица 4.3.
| Вид культуры | Посевная площадь | |
| В колхозах | В совхозах | |
| Зерновые Технические Картофель и овощебахчевые Кормовые | 56,9 10,5 2,8 29,8 | 64,4 3,7 1,9 30,0 |
| Итого | 100,0 | 100,0 |
Из табл. 4.5 видно, что в совхозах на каждые 100 га посевных площадей зерновые культуры занимают на 7,5 га больше, чем в колхозах, а удельный вес посевных площадей, используемых под техническими культурами, картофелем и овощебахчевыми культурами, в колхозах выше, чем в совхозах.
Выявленная специфика использования посевных площадей получает наглядность в графическом представлении. Для графического изображения относительных величин структуры обычно используются секторные диаграммы, в которых каждый сектор занимает площадь круга пропорционально удельному весу отображаемых частей целого. Применительно к условию данной задачи диаграмма будет состоять из двух кругов – площадь колхозов и совхозов, принимаемая на 100%. Для выделения в каждом круг четырех секторов (по числу культур) определим по данным об удельных весах посевных площадей, занятых под отдельными культурами, соответствующие значения центральных углов (1%=3,6):
Посевная площадь зерновых культур:
в колхозах в совхозах

 .
.
Посевная площадь технических культур:
в колхозах в совхозах

 .
.
Посевная площадь картофеля и овощебахчевых культур:
в колхозах в совхозах

 .
.
Посевная площадь кормовых культур:
в колхозах в совхозах

 .
.
 При помощи транспортира разделим круг на сектора соответственно значениям полученных центральных углов.
При помощи транспортира разделим круг на сектора соответственно значениям полученных центральных углов.

Рис. 4.2. Структура посевных площадей в колхозах и совхозах области по состоянию на 1 ноября 2006 г. (в процентах).
Относительная величина сравнения характеризует соотношение частей изучаемой совокупности, которое показывает, во сколько раз сравнимая часть является больше или меньше части, принимаемой за базу сравнения.
Задача. За истекший год получены следующие данные о численности детей, родившихся в области, чел.:
мальчики – 40357; девочки – 38019.
Для определения относительной величины сравнения численности мальчиков и девочек сопоставим между собой исходные данные (приняв за базу сравнения численность родившихся девочек):

т.е. на каждые 100 девочек рождалось 106 мальчиков.
Относительные величины динамики характеризуют развитие изучаемого явления во времени. Они позволяют при анализе данных, характеризующих развитие явления во времени, выявлять направление развития и измерять темпы роста.
Относительные величины динамики (темпы роста) исчисляются как отношения абсолютных (или средних) уровней ряда и выражаются в форме коэффициентов или процентов.
Задача. Потребление кожаной обуви в стране характеризуется следующими данными (на душу населения; пар в год):
2001 2002 2003 2004 2005 2006
0,4 1,1 1,9 2,4 3,0 3,2
Для анализа потребления обуви требуется определить относительные величины динамики.
Для выявления направления и характера изменений потребления обуви по сравнению с 2001 годом определим базисные темпы роста (Кб): 
где yi – уровень изучаемого периода; y0 – базисный уровень.
Последовательно сравним уровни 2002, 2003, 2004, 2005г., yi с уровнем 2001г. y0:
2002  2004
2004  2006
2006 
2003  2005
2005 
Из полученных базисных относительных величин динамики (темпов роста) видно, что за указанные годы потребление обуви в стране неуклонно возрастало:
2,75 < 4,75 < 6,0 < 7,5 < 8,0.
В 2006 году потребление на душу населения было в 8 раз больше, чем в 2001г.. Для выявления характера изменений потребления обуви по отдельным периодам (этапам) экономического развития произведем расчет цепных темпов роста Кц:
 ,
,
где yi – уровень изучаемого периода; yi-1 – уровень предшествующего периода.
Определим цепные темпы роста:
2002  2004
2004  2006
2006 
2003  2005
2005 
Из полученных цепных относительных величин динамики (темпов роста) видно, что по отдельным этапам экономического развития также происходило увеличение потребления обуви населением.
Представим исходные уровни ряда динамики в виде столбиковой диаграммы (рис.4.3).
Рис.4.3. Потребление кожаной
обуви на душу населения
 в стране в 2002-2006гг.
в стране в 2002-2006гг.
(в год пар).
 |
Рис. 4.4. Темпы роста потребления обуви
(кожаной) в 2001-2006гг. в год на
душу населения (в % к 2001г.).
Данная форма графического изображения уровней ряда динамки удобна тем, что расстояние столбиков (прямоугольников) друг от друга не зависит от величины интервалов времени.
Представим графически полученные в расчетах базисные относительные величины динамики. Для этой цели чаще всего используется линейная диаграмма (рис.4.4.).
В системе координат нанесем на ось ординат базисные темпы роста (в процентах), а на ось абсцисс – показания времени.
Из данного графика видно, что положение кривой определяется не только значениями базисных темпо роста, но и интервалами времени между датами.
Относительные величины интенсивности характеризуют степень насыщенности изучаемым явлением определенной среды. Они выражают соотношение разноименных, но связанных между собой величин и исчисляются как отношение величины изучаемого явления к объекту той среды, в которой происходит развитие явления. Относительные величины интенсивности являются именованными числами и могут выражаться в кратных отношениях, процентах, промилле и других формах.
Задача. Имеются следующие данные по району: число родившихся за год детей составляет 1701 человек; среднегодовая численность населения 94980 человек. определить относительную величину интенсивности, характеризующую рождаемость детей.
Для решения задачи определим коэффициент рождаемости детей.
Коэффициент = число родившихся = 1701 = 0,018 или 18% (промилле)
рождаемости среднегодовая чис- 94980
леность населения
Таким образом, рождаемость детей в районе в расчете на 1000 человек населения оставляла 18 человек.
Изученный материал по данной теме следует использовать при решении задач №2 вариантов №2, 4, 5, 6, 7, 8, 9, 10.
Тема 5. Cредние величины и показатели вариации.
По данной теме предусматривается решение следующих типов задач: исчисление средней арифметической простой и взвешенной, средней гармонической, моды и медианы.
В процессе изучения общественных явлений возникает необходимость выявить их общие свойства, типичные размеры и характерные признаки.
Средняя величина отражает общее, характерное и типичное для совокупности, благодаря взаимопогашению в ней случайных, нетипичных различий между признаками отдельных ее единиц. Различают несколько видов средних величин, рассмотрим среднюю арифметическую (простую и взвешенную) и среднюю гармоническую моду и медиану, расчет которых наиболее часто встречается в практической работе.
Пример: выработка продукции одним рабочим в день (руб.)
| Табельный номер рабочего | Выработано продукции | Варианты |
| X1 | ||
| X2 | ||
| X3 | ||
| X4 | ||
| X5 | ||
| Итого: 750 |
Средняя арифметическая простая рассчитывается тогда, когда цифровая величина признака у каждой единицы различна. Отдельные значения признака называются вариантами и обозначаются через x, число единиц в совокупности обозначается через n, среднее значение признака, -  .
.


| Число рабочих | Выработано продукции (1 рабочим), руб. |
| Итого: 30 чел. |
Если одно и тоже значение признака повторяется у нескольких единиц, то применяется средняя арифметическая взвешенная величина.
Число одинаковых значений называется частотой повторений или весами, обозначается символом f.
Формула средней арифметической взвешенной имеет вид: 

В ряде случаев числовое значение признака может быть выражено не конкретным числом, а интервалом «от» и «до».
| Группы рабочих по количеству произведенной продукции за смену, шт. | Число рабочих | Середина интервала |
| до 5 5 – 7 7 – 9 9 – 11 свыше 11 | ||
| Итого: |
Чтобы рассчитать среднюю выработку ( ):
):
1. В начале рассчитать среднюю по каждой группе, например, для второго интервала 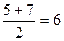 и т.д.
и т.д.
2. Величина интервала 1 группы равна величине интервала последующей группы, а величина интервала последней группы равна величине интервала предыдущей группы; например, рассмотрим интервал «до 5», 7-5=2, 5-2=3, значит интервал в первой группе как бы от 3 до 5, его середина – 4. Чтобы определить величину интервала «свыше 11», смотрим на предыдущий интервал. Его величина 11-9=2, следовательно, наш интервал будет от 11 до 13, его середина – 12.
Теперь используем формулу средней арифметической взвешенной

Таким образом средняя выработка 1 рабочего за смену – 7,5 шт.
Средняя гармоническая применяется в тех случаях, когда непосредственные данные о весах отсутствуют, а известно числовое значение усредняемого признака x и произведение числовых значений на количество единиц, обладающих данным его значением M(M=xf), например, при определении средней трудоемкости продукции, средней продолжительности чего-либо рода деятельности, при определении средних цен и т.д.
Формула средней гармонической имеет вид:
 где
где  - средняя величина; M=xf; 1/x – обратные значения.
- средняя величина; M=xf; 1/x – обратные значения.
Пример: Три партии материала А куплены по разным ценам 5, 10 и 15руб., требуется определить среднюю покупную цену материала А за килограмм, в первой партии куплено 100кг. за 500руб., во второй партии – 200кг. за 2000руб., а в третьей – 300кг. за 4500руб.. Если при исчислении средней цены за веса принять количество товаров, то верный результат даст средняя арифметическая:

Если в числовых значениях применять стоимость партий, то верный результат дает средняя гармоническая:

Характеристиками вариационных рядов наряду со средними являются мода и медиана.
Мода(Мо) – числовая величина признака (варианта) наиболее часто повторяющаяся в изучаемой совокупности. Для дискретных рядов распределения модой будет значение варианта с наибольшей частотой.
Например: Распределение проданной обуви по размерам характеризуется следующими показателями:
Размер обуви 36 37 38 39 40 41 42 43 44 45 и выше
Число пар к итогу, в % - 1 6 8 22 30 20 11 1 1
В этом ряду распределения мода рана – 41, именно этот размер обуви пользовался наибольшим спросом у покупателей.
Для интервальных рядов распределения с равными интервалами мода определяется по формуле:

где Mo – мода
XMo – начальное значение интервала, содержащего моду;
IMo – величина модального интервала;
fMo – частота модального интервала;
fMo-1 – частота интервала, предшествующего модальному;
fMo+1 – частота интервала, следующего за модальным.
Например. Распределение предприятий по численности промышленно-производственного персонала характеризуется следующими данными:
| Группы предприятий по числу работающих (чел.) | Число предприятий | Группы предприятий по числу работающих (чел.) | Число предприятий |
| 100 – 200 200 – 300 300 – 400 400 - 500 | 500 – 600 600 – 700 700 - 800 | ||
| Итого: |
В этой задаче наибольшее число предприятий (30) имеет численность работающих от 400 до 500 человек. Следовательно, этот интервал является модальным интервалом ряда распределения.
Введем обозначения: XMo=400; IMo=100; fMo=300; fMo-1=7; fMo+1=19.
Подставим эти значения в формулу моды и произведем вычисления:

таким образом модальный признак в данной совокупности варианта (числовое значение), расположенная в середине вариационного ряда.
Если ряд распределения дискетный и имеет нечетное число членов, то медианой будет варианта, находящаяся в середине упорядоченного ряда, построенного в возрастающем или убывающем порядке. Например, стаж пяти рабочих составил 2, 4,6, 7, 8 и 10 лет. В этом ряду имеются две варианты, стоящие в центре ряда. Это варианты 6 и 7. средняя арифметическая из этих значений и будет медианой ряда.

Изученный материал по данной теме следует использовать при решении задач №1 варианта №6, №3 вариантов №2, 7, 8, 10 и №4 вариантов №3, 4.
Тема 6. Ряды динамики.
Ряд статистических показателей, характеризующих изменение явлений во времени, называется рядом динамики. В зависимости от времени, которое характеризует явление, различают: моментный ряд динамики (данные на определенный момент времени – на начало месяца, квартала, года), если данные содержатся за определенный период времени – сутки, месяц, год и т.д. интервальный (периодический) ряд.
Прежде чем определить средний уровень динамического ряда, надо правильно определить его вид, т.е. от вида ряда зависит и способ исчисления среднего уровня.
Средний уровень моментного ряда исчисляется двумя способами:
1. по средней хронологической (для ряда динамики, где периоды между датами равны).
2. по средней арифметической взвешенной, где периоды между датаи различны.
Пример 1. Остаток материалов на складе завода (тыс.руб.):
на 01.01 на 01.02 на 01.03 на 01.04
60 65 70 50
Определяем вид ряда динамики – моментальный, с равностоящими по времени интервалами, следовательно, используем формулу средней хронологической, она имеет вид:
 ; где
; где  - средний уровень ряда;
- средний уровень ряда;
n – число уровней;
x – абсолютное значение уровня ряда.
 - среднеквартальный остаток материалов на складе.
- среднеквартальный остаток материалов на складе.
Пример 2. остаток материалов на складе завода (тыс.руб.):
на 01.01 на 01.03 на 01.11 на 01.01 сл.года
67 80 65 65
Определяем вид ряда динамики – моментный, с неравностоящими по времени уровнями, следовательно, используем формулу средней арифметической взвешенной, она имеет вид:
 где f – число месяцев между моментами времени равно 2, 8, 2.
где f – число месяцев между моментами времени равно 2, 8, 2.
 -среднегодовой остаток материалов на складе
-среднегодовой остаток материалов на складе
Завода.
Средний уровень периодического ряда динамики определяется по средней арифметической простой, ее формула: 
Пример 3. Произведено продукции в цехе завода (тыс.руб.).
январь февраль март
800 850 870
Среднеквартальный выпуск

В периодических рядах динамики рассчитывают следующие показатели рядов динамики:
1. абсолютный прирост (∆y);
2. темпы роста (К);
3. темпы прироста (∆К);
4. абсолютное значение одного процента прироста (А%).
Абсолютный прирост показывает на сколько единиц в абсолютном выражении каждый последующий уровень больше или меньше предыдущего.
Величина абсолютного прироста (∆y) определяется как разность между уровнем изучаемого периода yi уровнем, принимаемым за базу сравнения yo.
По базисной системе абсолютный прирост ∆y будет равен: ∆y= yi- yo.
По цепной системе абсолютный прирост ∆y будет равен: ∆y= yi-yi-1.
Темп роста показывает сколько % составляет последующий уровень по сравнению с базисным (предыдущем) уровнем, а если темп роста выражен в коэффициенте, то отвечает на вопрос во сколько раз.
Темп роста (К). величина этого показателя определяется из сопоставления уровня изучаемого периода yi с уровнем yo, который принимается за базу сравнения. Выражается в процентах или коэффициентах.
По базисной системе сравнения (база сравнения постоянная) темп роста (Кб) определяется: 
По цепной системе сравнения темп роста (Кц) определяется (за базу сравнения принимается предыдущий уровень ряда динамики yi-1): 
Темп прироста показывает на сколько % изменился последующий уровень по сравнению с базисным (предыдущим) уровнем и определяется:
∆К=К-100%.
Темп прироста ∆К. величина этого показателя определяется из сравнения в отношении абсолютного прироста ∆y с уровнем, принимаемым при анализе за базу сравнения.
Определяя по базисной системе сравнения темпы прироста (∆Кб) в качестве базы сравнения берется постоянный уровень yo.

Определяя по цепной системе сравнения темпы прироста (∆Кц) в качестве базы сравнения выступает уровень предшествующего периода yi-1.

Абсолютное значение 1% прироста показывает, что скрывается за 1% прироста в абсолютном выражении. Абсолютное значение 1% прироста определяется по формуле  , где yi-1 – уровень ряда, предшествующий данному.
, где yi-1 – уровень ряда, предшествующий данному.
Показатель абсолютного значения 1% прироста (А%) определяется путем отношения (в каждом периоде) абсолютного прироста (∆yц) к темпу прироста (∆Кц). расчет этого показателя имеет экономический смысл только по цепной системе:

Пример 4. произведено продукции в цехе завода, тыс.руб.
2004 2005 2006
100 110 130
П2005=110-100=10 тыс.руб., П2006=130-110=20 тыс.руб.
Производство продукции на предприятии в 2006г. по сравнению с 2004г. увеличилось на 10 тыс.руб., а в 2006г. по сравнению с 2005г. увеличилось на 20 тыс.руб..
К  или 110%. Производство продукции на предприятии в 2005г. по сравнению с 2004г. увеличилось в 1,1 раза или составило 110% от уровня 2004г.
или 110%. Производство продукции на предприятии в 2005г. по сравнению с 2004г. увеличилось в 1,1 раза или составило 110% от уровня 2004г.
Аналогично дается расчет и вывод по 2006г.
∆К2005=110-100=10%. Производство продукции в 2005г. по сравнению с 2004г. увеличилось на 10%.
Аналогично дается расчет и вывод по 2006г.
А2005=10/10%=1 тыс.руб. 1% прироста промышленной продукции в 2005г. составил 1 тыс.руб.
Для определения среднего изменения абсолютных приростов исчисляется показатель среднегодового абсолютного прироста  . Способы расчета среднего абсолютного прироста зависят от характера исходных данных.
. Способы расчета среднего абсолютного прироста зависят от характера исходных данных.
Если абсолютный прирост рассчитан по цепной системе сравнения, то средний абсолютный прирост определяется по средней арифметической простой 
Так, для данного примера этот расчет будет следующим:

Средний абсолютный прирост можно исчислить и непосредственно по абсолютным показателям динамики (y) по формуле: 
где m – число учетных единиц времени в ряду динамики.
Для данного примера 
В тех случаях, когда абсолютный прирост рассчитан по базисной системе сравнения (∆yб), расчет среднего абсолютного прироста производится по формуле:

В рассматриваемой задаче последний показатель абсолютного прироста (∆yn) составил 30 тыс.руб.. тогда среднегодовой уровень абсолютного прироста составил:

Изученный материал по данной теме следует использовать при решении задач №2 варианта №3 и задач №3 вариантов №1, 5, 6.
Тема 7. Индексы.
Индексы представляют собой показатели, позволяющие анализировать изменения явления во времени и пространстве, а так же оценивать степень выполнения плана. Следовательно, индексами являются любые относительные величины трех видов: динамики, сравнения, степени выполнения плана.
Индексы, исчисляемые отдельно по каждому элементу совокупности, называются индивидуальными (i). Если же индексы вычислены по всей совокупности, элементы которой не подаются непосредственному суммированию, они называются общими (групповыми). Такая форма индекса называется агрегатной. Например:  . При построении общих индексов (агрегатной формы) необходимо помнить следующие правила:
. При построении общих индексов (агрегатной формы) необходимо помнить следующие правила:
1. Обычно индекс определяется сопоставлением соизмеримых показателей, которые состоят из 2 или более элементов. Один элемент должен всегда быть изменяемым и называется он индексируемой величиной. В общем индексе (групповом) физического объема индексируемой величиной будет, например, выпуск продукции в ноябре и декабре (q1; qo).
2. Другой элемент (другие элементы) должен быть постоянным и называется весами индекса. В общем индексе физического объема выпуска изделий, весами будет цена за одно изделие в базисном периоде po. Если в качестве весов берется количественный показатель, он всегда отчетного периода, если качественный показатель, он всегда берется базисного периода.
Пример:
| Виды продукции | Свободная отпускная цена предприятия за 1 шт., руб. | Выпуск продукции, шт. | ||
| ноябрь p0 | декабрь p1 | ноябрь q0 | декабрь q1 | |
| А | ||||
| В |
Индивидуальный индекс физического объема показывает как изменяется размер производства отдельного продукта. Данные о производстве того или иного продукта есть соизмеримые величины, их можно просуммировать, т.к. они относятся к одной и той же потребительской стоимости, выражаются в одной и той же натуральной единице.
Индивидуальный индекс физического объема рассчитывается по формуле:
 .
.  или 125%;
или 125%;  или 117%.
или 117%.
Выпуск изделия А в декабре по сравнению с ноябрем возрос на 25%, а изделия В – на 17%.
Аналогично определяются индивидуальные индексы цен -  .
.
 или 110%;
или 110%;  или 80%.
или 80%.
Цены на изделие А в декабре по сравнению с ноябрем возросли на 10%, а на изделие В снизились на 20%.
Общий индекс физического объема – это относительная величина, которая получается путем сравнения нескольких вдов продукции, которые нельзя непосредственно суммировать. Формула общего индекса физического объема имеет следующий вид:
 , где ∑q1po – стоимость продукции отчетного периода;
, где ∑q1po – стоимость продукции отчетного периода;
∑qopo – стоимость продукции базисного периода.
 (121,4%).
(121,4%).
В декабре по сравнению с ноябрем выпуск продукции увеличился на 21,4%, 42500-35000=7500 руб.
Абсолютная сумма отклонения за счет изменения физического объема продукции составила 7500 руб.
Для исчисления общего индекса цен используется следующая формула:
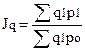 , где ∑q1p1 – стоимость продукции в отчетном периоде;
, где ∑q1p1 – стоимость продукции в отчетном периоде;
∑q1po - стоимость продукции, которая была бы в отчетном
периоде, цены остались базисного периода.
 (97,6%).
(97,6%).
В декабре по сравнению с ноябрем цены на продукцию снизились на 2,4; чтобы рассчитать экономию или перерасход за счет изменения цен, необходимо найти разность между числителем и знаменателем общего индекса цен Э=∑q1p1 - ∑q1po; Э=41500-42500=1000 руб. За счет снижения цен на 2,4% получена экономия (у потребителя) в сумме 1000 руб.
Всякий агрегатный индекс может быть преобразован в средний арифметический из индивидуальных индексов.
Так индивидуальный индекс физического объема  , откуда q1=iqo.
, откуда q1=iqo.
Следовательно, преобразование агрегатного индекса физического объем в средний арифметический будет иметь вид:  .
.
Этот индекс применяется в том случае, когда известна стоимость продукции базисного периода, но не известно количество продукции в натуральном выражении в отчетном периоде.
Средний гармонический индекс цен легко можно получить из индивидуальных индексов цен.
Так, индивидуальный индекс цен равен:  , отсюда
, отсюда  .
.
Следовательно, преобразование агрегатного индекса цен в средний гармонический имеет вид: 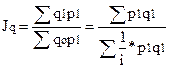 .
.
Средний гармонический индекс цен применяется в том с
Date: 2016-01-20; view: 709; Нарушение авторских прав