Фазовые характеристики

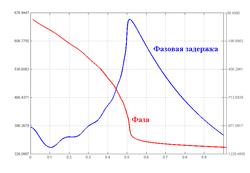
Рис. Типовая ФЧХ и фазовая задержка фильтра Чебышёва I рода 10-го порядка.

Фазовые характеристики фильтра Чебышёва I рода — фазо-частотная характеристика (ФЧХ) и фазовая задержка — представлены на рисунке. Фазо-частотная характеристика показывает распределение по частоте смещения фазы выходного сигнала относительно входного. Фазовая задержка определяется как частное от деления фазо-частотной характеристики на частоту и характеризует распределение по частоте временного смещения выходного сигнала относительно входного.

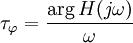
Временны́е характеристики

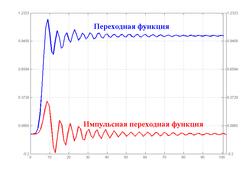
Рис. Типовые временные характеристики фильтра Чебышёва I рода 10-го порядка.

Временные характеристики фильтра Чебышёва I рода — импульсная переходная функция и переходная функция — представлены на рисунке. Импульсная переходная функция представляет собой реакцию фильтра на входной сигнал в виде дельта-функции Дирака, а переходная функция — реакцию на входное воздействие в виде единичной функции Хевисайда.
39.Инверсный фильтр Чебышева, вывод передаточной функции

Фильтр Чебышёва II рода (инверсный фильтр Чебышёва) используется реже, чем фильтр Чебышёва I рода ввиду менее крутого спада амплитудной характеристики, что приводит к увеличению числа компонентов. У него отсутствуют пульсации в полосе пропускания, однако присутствуют в полосе подавления. Амплитудная характеристика такого фильтра задаётся следующим выражением:

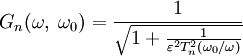
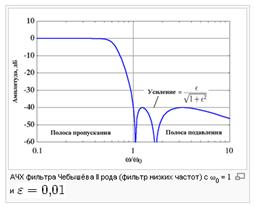
В полосе подавления полиномы Чебышёва принимают значения от 0 до 1, из-за чего амплитудная характеристика такого фильтра принимает значения от нуля до

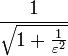
минимальной частотой, при которой достигается этот максимум является частота среза ω₀. Параметр связан с затуханием в полосе подавления γ в децибелах следующим выражением:

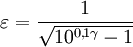
Для затухания на частотах полосы подавления в 5 дБ: ; для затухания в 10 дБ: . Частота f_C = ω _C / (2π) является частотой среза. Частота затухания в 3 дБ f_H связана с f_C следующим выражением:

.

Логарифм модуля амплитудной характеристики фильтра Чебышёва II рода восьмого порядка на комплексной плоскости (s = σ + j ω) с 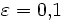и ω₀ = 1. Белые пятна соответствуют полюсам, а чёрные — нулям. Показаны все 16 полюсов. 6 нулей (все нули второго порядка) показаны также, 2 находятся за пределами картинки (один на положительной мнимой оси, другой — на отрицательной мнимой оси). Полюса передаточной функции фильтра — это полюса, находящиеся в левой полуплоскости, нули передаточной функции — это нули модуля амплитудной характеристики фильтра Чебышёва, только не второго, а первого порядка. Чёрный цвет соответствует коэффициенту усиления менее 0,01, белый — коэффициенту усиления более 3.

Приняв частоту среза равной единице, получим выражение для полюсов (ω _pm) фильтра Чебышёва:

.

Полюса фильтра Чебышёва II рода представляют собой «инверсию» полюсов фильтра Чебышёва I рода:

,

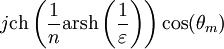где .

Нули (ω _zm) фильтра Чебышёва II рода определяются из следующего соотношения::

.

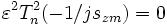Нули фильтра Чебышёва II рода являются «инверсией» нулей многочленов Чебышёва:

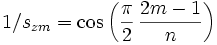, где .

Передаточная функция задаётся при помощи полюсов в левой полуплоскости комлексной плоскости, её нули совпадают с нулями модуля амплитудной характеристики, с тем лишь отличием, что их порядок равен 1.

Date: 2016-02-19; view: 686; Нарушение авторских прав