
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Уравнения состояния
|
|
Параметры состояния термодинамической системы связаны между собой зависимостью, которая называется уравнением состояния. Это уравнение устанавливает функциональную зависимость параметров состояния f(р,T,v)=0. С математической точки зрения функция f(р,T,v)=0 в трехмерном пространстве описывает конкретную поверхность, каждая точка на которой отображает равновесные состояния ТДС. Эта поверхность называется термодинамической поверхностью. Уравнение состояния позволяет символично выразить каждый из параметров через два других параметра, т.е.
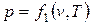 ;
; 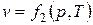 ;
; 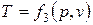 .
.
Следует отметить, что современная физика пока не располагает универсальным уравнением состояния для всех форм материальных тел. На сей день имеется ряд эмпирически установленных зависимостей для некоторых категорий материальных тел, описывающих их термодинамическое состояние.
Для идеального газа эта зависимость называется уравнением Клапейрона и имеет вид:
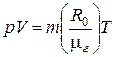 ,
,
где р – давление, (Па); V – объем газа, (м3); m – масса газа, (кг); R0 =8314 (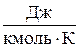 ) - универсальная газовая постоянная,
) - универсальная газовая постоянная, 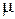 г – мольная масса газа, (
г – мольная масса газа, ( ); Т – абсолютная температура, (К).
); Т – абсолютная температура, (К).
Если использовать понятие удельного объема 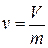 , то вышеприведенное уравнение можно написать в виде
, то вышеприведенное уравнение можно написать в виде
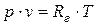 ,
,
где 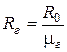 , (
, (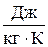 ),- удельная газовая постоянная, характеризует физические свойства конкретного газа. Для некоторых газов их свойства представлены в табл. 1.1.
),- удельная газовая постоянная, характеризует физические свойства конкретного газа. Для некоторых газов их свойства представлены в табл. 1.1.
Таблица 1.1
| Газ | μ, кг/кмоль | R, Дж/(кг К) | ρ0, кг/м3 |
| Водород Н2 | 0,09 | ||
| Гелий Не | 0,18 | ||
| Азот N2 | 1,25 | ||
| Кислород О2 | 1,43 | ||
| Воздух | 29,1 | 1,29 | |
| Углекислый газ СО2 | 1,81 | ||
| Водяной пар Н2О | 0,71 |
Для реальных газов, в которых необходимо учитывать межмолекулярные силы взаимодействия и нельзя пренебрегать объемами молекул. Соответствующее уравнение состояния было предложено Ван-дер-Ваальсом, которое имеет вид
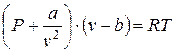 ,
,
где а – учитывает силу взаимодействия молекул,
b – представляет собой суммарный объем молекул.
Частными случаями уравнения Клапейрона являются законы идеального газа:
1. Закон Бойля-Мариотта – произведение абсолютного давления газа на его удельный объем, при T= const, есть величина постоянная (рv= const).
Таким образом, для двух последовательных состояний газа согласно этому закону, имеем:
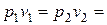 const
const 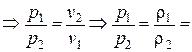 const
const
2. Закон Гей-Люссака – отношение удельного объема газа, при р= const, к абсолютной температуре есть величина постоянная (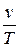 =const).
=const).
Тогда для двух последовательных состояний газа имеем:
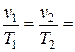 const,
const, 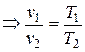 ,
, 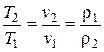 .
.
3. Закон Шарля - при v= const отношение температуры к давлению есть величина постоянная ( const). Для двух последовательных состояний имеем:
const). Для двух последовательных состояний имеем:
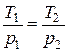 .
. 
Date: 2016-02-19; view: 368; Нарушение авторских прав