Конспект вопроса 4

Подобия плоскости и их свойства. Классификация подобий. Группа подобий и ее подгруппы. Применение подобий к решению задач элементарной геометрии.

Литература Атанасян С.Л. Геометрия 1: – Москва, 2001. §§ 39 – 41

Определение 1. Преобразование f плоскости называется подобием, если для любых двух её точек A и В выполнено условие:

½f(A) f(B)½ = k ½AB½, (39.1)

где k постоянное число, большее нуля.

Определение 2. Пусть на плоскости дана точка O. Под гомотетией с центром в точке О и коэффициентом m понимается такое отображение точек плоскости на себя, при котором каждой точке A ставится в соответствие точка A¢, удовлетворяющая условию:

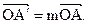(39.2)

где m постоянное число, отличное от нуля.

Легко видеть, что гомотетия является преобразованием плоскости. Если m = 1, то согласно (39.2), 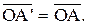, поэтому в этом случае гомотетия совпадает с тождественным преобразованием. Если m = -1, то 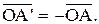и гомотетия представляет собой центральную симметрию относительно точки O. Гомотетию с центром в точке О и коэффициентом m будем обозначать через .

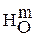Свойство 1. Гомотетия 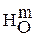- подобие с коэффициентом ½m½.

Доказательство. Рассмотрим точки A и B. Пусть A' = 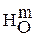(A), B' = 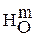(B). Тогда . Из формулы (39.2) следует, что

.

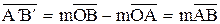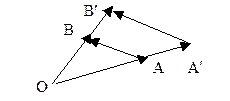
Поэтому A'B' = mAB. Свойство доказано.

Свойство 2. Множество всех гомотетий с фиксированным центром образует группу преобразований.

Date: 2016-02-19; view: 362; Нарушение авторских прав