Вторая линейная операция – произведение вектор на число

Обзорные лекции по геометрии

Конспекты

Вопрос № 1

Векторы на плоскости и в пространстве. Линейные операции над векторами, координаты векторов. Скалярное, векторное и смешанное произведение векторов. Применение свойств векторов к решению задач элементарной геометрии.

План ответа

1. Направленные отрезки и векторы и их свойства.

2. Линейные операции над векторами, свойства.

3. Координаты векторов на плоскости и в пространстве.

4. Скалярное произведение векторов.

5. Векторное произведение векторов.

6. Смешанное произведение векторов.

7. Пример решения задачи элементарной геометрии с применением векторной алгебры.

Отрезок называется направленным, если для него указан порядок его концов. Первый из них называется началом, а второй концом направленного отрезка.). Если M начало, а N конец направленного отрезка, то будем его обозначать через .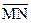

Определение 1. Направленные отрезки, расположенные на одной прямой или параллельных прямых, называются коллинеарными.

Определение 2. Если коллинеарные направленные отрезки имеют одинаковые направления, то они называются сонаправленными, если их направления различны, то - противоположно направленными.

Признак сонаправленности отрезков: пусть 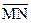и коллинеарные направленные отрезки, не лежащие на одной прямой, они сонаправлены тогда и только тогда, когда их концы N и Q лежат в одной полуплоскости относительно прямой MP, проходящей через их начала (рис. 1 а).

Отсюда следует, что тогда и только тогда, когда отрезки MP и NQ не пересекаются. Если 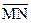и противоположно направлены и не лежат на одной прямой, то их концы N и Q принадлежат различным полуплоскостям относительно прямой MP. Таким образом в том и только в том случае, когда отрезки MP и NQ пересекаются (рис. 1 б).

Направленный отрезок называется нулевым, если его начало совпадает с его концом. У такого отрезка длина равна нулю, считается, что его направление произвольное, т.е. он сонаправлен с любым отрезком.

Определение 3. Два ненулевых направленных отрезка называются равными друг другу, если они сонаправлены и их длины одинаковы. Два нулевых направленных отрезка всегда равны между собой.

Свойство 1. Отношение равенства направленных отрезков является отношением эквивалентности.

Выполняются свойства рефлексивности, симметричности и транзитивности.

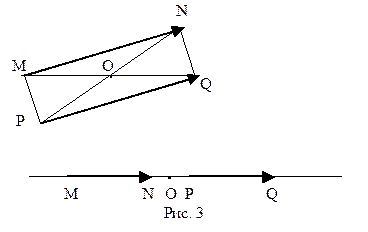Свойство 2. Отрезок равен отрезку в том и только в том случае, когда середины отрезков AD и BC совпадают (рис. 3).

Свойство 3. Отрезок равен отрезку тогда и только тогда, когда .

Свойство 4. Если даны направленный отрезок и точка С, то существует единственная точка D, для которой .

Определение 4. Вектором называется класс равных между собой направленных отрезков.

Как следует из определения 3, все равные между собой направленные отрезки имеют одну и ту же длину, Её мы будем называть длиной или модулем вектора. и обозначать через или . Модуль нулевого вектора равен нулю.

Векторы назовем соответственно коллинеарными, сонаправленными или противоположно направленными, если коллинеарны, сонаправлены или противоположно направлены любые два его представителя. Очевидно, что это определение не зависит от выбора представителей векторов. Обозначать коллинеарные, сонаправленные и противоположно направленные векторы будем соответственно через: Если два вектора имеют одинаковый модуль, но противоположные направления, то их будем называть противоположными. Вектор, противоположный будем обозначать через (- ).

Легко видеть, что все нулевые направленные отрезки равны между собой. Действительно, у каждого из них длина равна 0 и они сонаправлены друг с другом. Вектор, представителем которого является нулевой направленный отрезок, называется нулевым. Он будет нами обозначаться через .

Определение 1. Пусть даны векторы и .От точки А отложим вектор , а от конца направленного отрезка отложим вектор . Вектор , определенный направленным отрезком , называется суммой векторов и : .

Способ определения суммы векторов - правило параллелограмма.

Свойство 1. Для любых векторов и справедливо равенство: . (свойство коммутативности).

Свойство 2. Для любых векторов и выполнено равенство: (свойство ассоциативности).

Свойство 3. Для любого вектора выполнено соотношение: .

Свойство 4. Для любого вектора его сумма с противоположным вектором равна нулевому вектору: .

Определение 2. Под разностью двух векторов понимается вектор , удовлетворяющий условию: .

Вектор

Вторая линейная операция – произведение вектор на число

Определение 1. Под произведением ненулевых числа l и вектора понимается такой вектор , который удовлетворяет следующим условиям:

1. , где - абсолютная величина l.
2. Если l > 0, то векторы и сонаправлены; если l < 0, то и противоположно направлены.

В случае когда l = 0, либо ,произведение .

Свойство 1. Пусть - произвольный вектор, тогда

(3.1)

Свойство 2. Для любых чисел a и b. И любого вектора справедливо равенство:

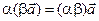. (3.2)

Свойство 3. Для любых чисел a и b и любого вектора справедливо равенство:

. (3.3)

Теорема 1. (теорема о коллинеарных векторах). Пусть даны векторы и , причем . Они коллинеарны в том и только в том случае, когда существует такое единственное число l., для которого .

Свойство 4. Для любого числа a и любых векторов и справедливо равенство:

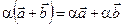
Определение 1. Вектор будем называть линейной комбинацией векторов с коэффициентами .

Определение 2. Система векторов называется линейно зависимой, если существуют такие числа среди которых, по крайней мере, одно отлично от нуля и что линейная комбинация равна нулевому вектору.

Если система векторов не является линейно зависимой, то она называется линейно зависимой.

Система линейно независима в том и только в том случае, когда из равенства следует:

Свойство 1. Если система содержит нулевой вектор, то она линейно зависима.

Свойство 2. Если в системе векторов содержится линейно зависимая подсистема, то вся система также линейно зависима.

Свойство 3. Система векторов линейно зависима тогда и только тогда, когда один из ее векторов линейно выражается через остальные.

Теорема 1. Два вектора линейно зависимы тогда и только тогда, когда они коллинеарны.

Компланарные системы векторов. Базис, координаты векторов

Будем говорить, что вектор параллелен плоскости , если его представитель параллелен или лежит в этой плоскости. Ясно, что это определение не зависит от выбора представителя .

Определение 3. Система векторов называется компланарной, если существует плоскость, которой параллельны все векторы системы.

Примеры компланарной системы векторов:

1. Если система . состоит из коллинеарных векторов, то она компланарная.

2. Система, состоящая из двух векторов, всегда является компланарной.

Определение 4. Система, состоящая из двух неколлинеарных векторов плоскости, заданных в определенном порядке, называется базисом плоскости.

Базис будем называть ортонормированным или прямоугольным декартовым, если его векторы взаимно перпендикулярны и имеют единичную длинну. Произвольный базис плоскости называется аффинным или общим декартовым.

(Теорема о разложении вектора плоскости по векторам базиса). Если на плоскости дан базис, то любой ее вектор линейно выражается через векторы базиса, причем коэффициенты разложения определяются единственным образом.

Теорема 3. (Теорема о компланарных векторах). Система, состоящая из трех векторов, линейно зависима тогда и только тогда, когда векторы компланарны.

Следствие. Система, состоящая из трех не компланарных векторов, линейно независима.

Введем основное понятие аналитической геометрии - координаты вектора.

Определение 5. Коэффициенты разложения вектора плоскости по векторам базиса называются координатами этого вектора относительно базиса.

Из теоремы 3 следует, что векторы, составляющие базис пространства, линейно независимы. Базис пространства называется прямоугольным декартовым, если его векторы взаимно перпендикулярны и имеют единичную длину. Произвольный базис пространства носит название аффинного или общего декартова.

Теорема 4. (Теорема о разложении вектора пространства по векторам базиса). Пусть в пространстве дан произвольный базис. Тогда любой вектор пространства линейно выражается через базисные векторы, причем коэффициенты разложения определяются единственным образом.

Определение 7.. Коэффициенты разложения вектора пространства по векторам базиса называются его координатами относительно этого базиса.

Теорема. Пусть на плоскости или в пространстве дан базис. Тогда координаты суммы двух векторов равны сумме их соответствующих координат, а координаты произведения вектора на число - произведению этого числа на соответствующие координаты вектора.

Теорема 7. Пусть координаты векторов и равны Они коллинеарны в том и только в том случае, когда

.

. Векторы и плоскости коллинеарны в том и только в том случае, когда их координаты пропорциональны.

Теорема 8. Два вектора пространства тогда и только тогда коллинеарны, когда их координаты пропорциональны.

Теорема 9. Пусть даны координаты векторов пространства Тогда эти векторы компланарны в том и только в том случае, когда

.

Date: 2016-02-19; view: 588; Нарушение авторских прав