Классификация ОТ и нахождение вычетов этих ОТ

Пусть z₀– изолированная ОТ. Рассмотрим ряд Лорана в окрестностях z₀()

Характер ОТ определяется главной частью ряда Лорана в ее окрестности

1) Главная часть ряда Лорана не содержит отрицательных степеней z₀ – устранимая точка (УСТ)

2) Если главная часть ряда Лорана в окр-ти особой точки z₀содержит бесконечное число слагаемых, то z₀называется существенной особой точкой.

3) Если главная часть ряда Лорана содержит конечное число слагаемых, то z₀называется полюсом порядкаn, гдеn – наивысший порядок отрицательной степени.

8. Обыкновенные дифференциальные уравнения (д.у.) 1-го порядка. Основные понятия. Задача Коши. Геометрический смысл задачи Коши. Теорема существования и единственности решения задачи Коши для д.у. 1-го порядка.

Обыкновенным д.у. 1-го порядка называется уравнение вида F(x,y,y’)=0, где y=y(x) – дифференциальная ф-я

Частным решением обыкновенного д.у. 1-го порядка F(x,y,y’)=0 назывется ф-я y=y(x), подстановка которой в ур-ие обращает его в верное равенство для всех Х из некоторого интервала (a,b).

Общим решением ур-ия F(x,y,y’)=0 назовем множество всех его частных решений. Если общее решение получено в неявном виде j(x,y)=C, то выражение j(x,y)=C называется общим интегралом уравнения.

Задача Коши для обыкновенного д.у. 1-го порядка – это задача нахождения частного решения уравнения F(x,y,y’)=0 при начальном условии у(х₀)=у₀.

Геометрический смысл решения задачи Коши для ур-ия 1-го порядка

Среди всех интегральных кривых д.у. F(x,y,y’)=0 решением задачи Коши будет кривая, которая проходит через точку (х₀,у₀), задаваемую начальным условием у(х₀)=у₀.

Интегральные кривые – графики всех частных решений.

Т. о существовании и единственности решения задачи Коши для уравнения

(1)

у(х₀)=у₀, (2)

Если в некоторой окрестности точки М(х₀,у₀,у’₀,…,y₀^(n-1)) ф-я и ее частная производная непрерывны в некоторой окрестности (x₀-h, x₀+h) точки х₀, то существует единственное решениеy=j(x), которое удовлетворяет уравнению (1) и условию (2).

9. Методы интегрирования основных д.у. 1-го порядка (линейные уравнения, уравнения Бернулли, однородные уравнения, уравнения в полных дифференциалах).

1) Уравнения с разделяющимися переменными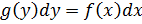

Метод решения:

2) Однородные д.у. первого порядка

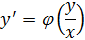
– уравнение с разделяющимися переменными

Метод решения:

3) Линейные уравнения 1-го порядка

(линейное по у) или (линейное по х)

Метод решения (метод Бернулли)

4) Ур-ия Бернулли

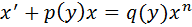
Метод решения (метод Бернулли)

5) Ур-ия в полных дифференциалах

Метод решения состоит в отыскании ф-ии j(х,у)=С, что

10. Обыкновенные д.у. n-го порядка. Теорема существования и единственности решения задачи Коши. Понятие общего решения.

Date: 2016-02-19; view: 306; Нарушение авторских прав