Основные элементарные функции и их свойства

1.

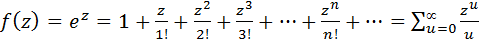
По определению функция e^z – это функция, представленная в виде ряда. Определение введено таким образом, чтобы разл. было справедливо для действительных значений X

Следствие: - формула Эйлера

Док-во:

Периодичность функции е^z , T= 2pi

Док-во:

.

T= 2pi

2.

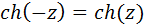– четная функция

3.

– нечетная функция

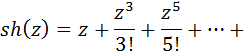
4.

– нечетная функция

5.

– четная функция

Все гиперболические функции периодичны с периодом T= 2pi. Все тригонометрические функции периодичны с периодомT= 2p.

6. W=zⁿ - степенная функция

7. Другие функции

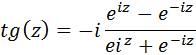
8. Обратные функции компл. переменной

3. Дифференцируемость ф-ии комплексной переменной W=f(z). Понятие аналитической функции в точке и области. Условия Коши-Римана.

Пусть W=f(z) определена в точке z₀ и в некоторой ее окрестности.

d - окрестность т.

Производной f(z) в точке z₀называется предел

Если функция имеет производную в т. z₀, то она называется дифференцируемой в этой точке.

Теорема необходимости и недостаточности условий дифференцируемости ф. W=f(z) в т. z₀ (условия Коши-Римана)

Пусть . Для того, чтобы W=f(z) была диф-ой в точке необходимо и достаточно, чтобы

Доказательство. Необходимость. Пусть диф-ма в точке z_0. Это означает, что – дифференцируемые ф-ии в т. (x₀,y₀) и
не зависит от способа приближения к z₀

Т.к. этот предел сущ-ет (и предположили, что ф. W=f(z) диф-ма по условию), то он не зависит от способа приближения zк z₀, т.е. Dz стремится к нулю.\

Dy=0(y=y₀)

Попробуем вычислить тот же предел по другому пути

Сравнивая этот результат с полученным ранее, имеем равенство

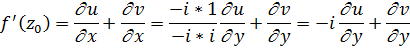
По определению равенства компл. чисел получим

Обратное утверждение (без док-ва) – достаточность

Если условие Коши-Римана выполняется в т. (x₀,y₀), то ф-я f(z) диф-ма в т.z_0.

Date: 2016-02-19; view: 345; Нарушение авторских прав