Выбор и обоснование модели для исследования технологического процесса

На основании имеющейся информации об объекте исследования необходимо выбрать модель, которая позволила бы разработать имитационную модель для исследования технологического процесса (объекта). При этом необходимо учитывать условия протекания процесса, режимы работы оборудования, технологические параметры процесса и т.д., особое внимание уделяется такой характеристике, как время, внешним и случайным воздействиям.

Совместно с математической моделью и выбранной моделью моделирования разрабатывается и представляется концептуальная модель, которая является основой для имитационной модели.

2.4.1 Динамические модели. В этой части первого раздела описывается разработанная математическая модель технологического процесса (объекта). Представление модели начинается с описания балансов: материального, энергетического, теплового и др. Определяются задачи математической модели, описываются входные, выходные параметры и возмущающие воздействия, устанавливается вид зависимости между ними.

Производственный процесс рассматривают как последовательную смену состояний технологических операций во времени, определяют входные и выходные переменные (рисунок 2.1). Для химико-технологических процессов входными переменными (факторами) являются физические параметры входных потоков сырья и т.п., а также параметры различных физико-химических воздействий окружающей среды, такие параметры называются управляющими воздействиями (Х₁, Х₂, …, Х_m). Выходными переменными (параметрами объекта автоматизации) служат физические параметры материальных и энергетических балансов (Y₁, Y₂, …, Y_n). Управляемые возмущающие воздействия – оперативные воздействия на изменение условий работы (М₁, М₂, …, М_К) и неконтролируемые возмущения (L₁, L₂, …, L_r).

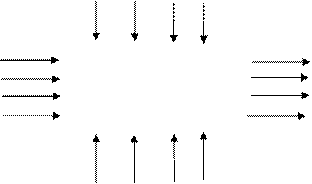
		М1	М2		МК
Х1	Внутренние параметры   z1(х,t); z2(х,t); …; zm(х,t)	Y1
Х2	Y2
Хm	Yn
		L1	L2		Lr

Рисунок 2.1 – Схема технологического объекта

Связь между входными и выходными параметрами с учетом действующих возмущений характеризуется математическими моделями, которые могут быть представлены в виде

Y₁, Y₂, …, Y_n=F(Х₁, Х₂, …, Х_m; М₁, М₂, …, М_К; L₁, L₂, …, L_r).

Выделение входных и выходных параметров весьма важно при исследовании динамики процессов химической и пищевой технологий. Используя эти понятия, можно сказать, что математическая модель, описывающая динамику технологического объекта, должна предсказывать, как будут меняться во времени выходные параметры при произвольном изменении во времени входных параметров. При этом любой технологический объект целесообразно интерпретировать как функциональный оператор, ставящий в соответствие каждому набору входных функций u₁(t), u₂(t),…, u_n(t) соответствующий набор выходных функций v₁(t), v₂(t),…, v_k(t).

Начиная с момента времени t=0, на вход объекта подается воздействие u(t). Тогда независимо от вида u(t) передаточная функция W(p) удовлетворяет соотношению

.

Здесь и - преобразования Лапласа от функций u(t) и v(t):

2.4.2 Статические модели. Далее представляется и описывается, разработанная на базе математической модели, имитационная модель технологического процесса (объекта). Приводится обоснование модели (статическая, динамическая). Знание динамических свойств объекта автоматизации позволяет обоснованно выбрать регуляторы для объекта и с помощью имитационной модели провести эксперименты, что невозможно сделать в реальных условиях. Статические характеристики, представляющие зависимость выходных переменных от входных воздействий в установившихся режимах, определяют нахождением для каждой выходной переменной статической зависимости ее от входных воздействий в виде уравнения регрессии:

, (4)

где b₀ – свободный член уравнения регрессии; b₁… b_n – коэффициенты регрессии, отражающие линейные эффекты; b₁₂… b_n-1,n – коэффициенты регрессии, отражающие парные взаимодействия; b₁₁… b_nn – коэффициенты регрессии, отражающие квадратичные эффекты и т.д.

2.4.3 Математическое описание объекта исследования. При решении задач идентификации исследуемого объекта используются аналитические и экспериментальные подходы.

В основе аналитического подхода лежит детальное изучение процессов, протекающих в объекте путем рассмотрения физико-химических закономерностей, превращений и т.д. Данный подход затрудняет учет всего многообразия факторов, поэтому математическим моделям, полученным аналитическим методом, свойственна идеализация.

В основе экспериментального подхода лежат методы активного и пассивного эксперимента. При пассивном эксперименте объект исследования находится в режиме нормальной эксплуатации при случайных отклонениях входных переменные и соответствующих им изменениях выходных переменных, которые фиксируются в случайные моменты времени. Затем полученные данные подвергаются статистической обработке.

x

Рисунок 2.1 – Совокупность экспериментальных данных при определении статической характеристики объекта исследования

Вид функции должен быть известен заранее, причем чаще всего рассматриваются модели первого и второго порядка /2/:

, (5)

. (6)

По результатам обработки совокупности экспериментальных данных методом наименьших квадратов определяют коэффициенты уравнения регрессии. В соответствии этим методом значение коэффициентов регрессии b₀, b₁ для модели (5)

где N – число опытов, определяются из условия минимума суммы квадратов отклонений.

(7)

где - измеренное и вычисленное значение выходной величины для i-го опыта.

Выражение (7) для исследуемой модели записывается в виде

Чтобы найти b₀ и b₁, при которых сумма S минимальна, возьмем производную от S по b₀ и b₁ и приравняем их к нулю. После преобразований получаем уравнения:

(8)

Совместное решение этих уравнений дает:

(9)

Пример 1. Пусть имеются экспериментальные данные из 9 опытов, представленных в таблице 2.1. Рассмотрим процедуру определения статической характеристики линейного объекта

.

Таблица 2.1 – Данные и обработка результатов эксперимента при определении статической характеристики объекта управления

№ опыта	Значение переменной х	Значение выходной характеристики y
1-й замер	2-й замер	3-й замер	Среднее значение по трем сериям (переменная состояния)
	Х1	Y11	Y12	Y13
	Х2	Y21	Y22	Y23
…	…	…	…	…	…
	Х9	Y91	Y92	Y93

В соответствии с уравнениями (9) для девяти равностоящих значений аргумента x по средним значениям из таблицы 2.1 рассчитываем коэффициенты регрессии по формулам:

Для определения b₀ рассчитывается среднее значение выходной переменной по всем (девяти) опытам:

Затем на графике 2.1 необходимо изобразить функцию y=f(x) результатов эксперимента по данным таблицы и расчетную характеристику , а затем проверить адекватность по критерию (7).

Часто на практике для исследования объекта используются временные ряды. Временные ряды для характеристики изменения выходной переменной объекта во времени представляют последовательность наблюдений некоторого явления на выходе объекта во времени. Отдельные наблюдения временного ряда называются его уровнями и обозначаются y₁, y₂,…y_N.

Цель анализа временного ряда – отыскание основной закономерности изменения рассматриваемого явления на выходе объекта во времени. Для выявления этой закономерности временной ряд необходимо сгладить. Полученная функция отражает основную тенденцию рассматриваемого явления во времени и называется трендом. Понятие тренда эквивалентно понятию математической модели объекта исследования. Сглаживание временных рядов осуществляется по методу скользящих средних, что позволяет получить графическое представление для тренда. При сглаживании временного ряда по данному методу, группы последовательных наблюдений ряда заменяются их средними арифметическими.

Пусть дан ряд y₁, y₂,…y_N с числом наблюдений во времени N. Зададим интервал сглаживания µ, это число, по которому берется среднее арифметическое. Пусть µ=3. Тогда сглаживание происходит следующим образом:

- вычисляется среднее по первым трем уровням – второе наблюдение

- вычисляется среднее по следующим трем уровням – третье наблюдение

- вычисляется среднее по следующим трем уровням – четвертое наблюдение

Очевидно, что сглаживание будет наиболее плавным, чем выше интервал сглаживания µ. Уровни временных рядов обрабатываются по методу суммы наименьших квадратов (7) для полинома второго порядка (6), заменив переменную x на t. Тогда система уравнений (8) будет иметь вид

(12)

Пример 2. Пусть имеется временной ряд, описанный выражением (6). Рассмотрим данную ситуацию на примере восьми опытов, представленную в таблице 2.2.

Таблица 2.2 – Данные и обработка результатов эксперимента при определении статической характеристики объекта управления

№ опыта	Значение переменной х	Значение выходной характеристики y
1-й замер	2-й замер	3-й замер	Среднее значение по трем сериям	Сглаженное значение
	Х1	Y11	Y12	Y13		-
	Х2	Y21	Y22	Y23
…	…	…	…	…	…	…
	Х8	Y81	Y82	Y83		-

Аналитическое уравнение тренда представляется в виде

.

Среднее значение выходной величины по всем опытам определяется как

По выражению (12) определяем коэффициенты регрессии:

.

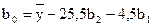Далее необходимо проверить адекватность полученного выражения тренда по критерию минимума суммы квадратов отклонений (7) S→min.

2.4.4 Определение динамических характеристик объекта исследования основывается на методах статистической динамики. Методы включают в себя определение некоторых характеристик.

Определение автокорреляционной функции R_x(τ) для функции времени x(t) является интеграл

.

Данное выражение тем точнее, чем больше интервал 2Т.

Взаимокорреляционной функцией R_xy(τ) для двух функций времени x(t) и y(t) является интеграл

.

Рассмотрим автокорреляционную функцию R_xy(τ) между входом x(t) и выходом y(t) объекта управления.

Для линейного объекта управления импульсную переходную функцию h^*(t) – реакцию выхода на единичный импульс входа – можно определить расчетом по известной автокорреляционной функции между входом и выходом объекта. Это определение осуществляется из следующего интегрального уравнения

. (13)

Вычислив автокорреляционную функцию R_x(τ) и взаимокорреляционную функцию R_xy(τ) входа и выхода можно решить уравнение (13) относительно импульсной переходной функции h^*(t). Решение которого можно свести к решению системы линейных алгебраических уравнений. Представим уравнение (13) в виде суммы

,

где Δt – малый фиксированный интервал времени.

Данное уравнение должно удовлетворяться при любых значениях τ. Найденная дискретная величина h^*(t) аппроксимируется суммой экспоненциальных, так как только они могут составлять переходную функцию линейного дифференциального уравнения.

Передаточную функцию объекта управления определяют по формуле преобразования Лапласа

.

При активном эксперименте на объекте исследования действуют типовые входные сигналы: ступенчатые, импульсные, гармонические. Соответственно этим воздействиям определяются временные характеристики (кривые разгона), импульсные и частотные характеристики.

Планирование эксперимента. Полный факторный эксперимент

2.5.1 Основные понятия и определения. Эксперимент с моделью на компьютере проводится с целью получения информации о характеристиках процесса функционирования рассматриваемого объекта. Эта информация может быть использована как для анализа характеристик, так и для оптимизации процесса при заданных ограничениях. В зависимости от цели моделирования могут быть реализованы на ЭВМ различные подходы к организации имитационного эксперимента.

Эффективность машинных экспериментов с моделью существенно зависит от выбора плана эксперимента, поскольку план определяет объем и порядок проведения вычислений на компьютере, приемы накопления и статистической обработки результатом моделирования. Основная задача планирования машинных экспериментов с моделью – получение информации об объекте моделирования при минимальных или ограниченных затратах машинных ресурсов на реализацию процесса моделирования. Преимущества машинного планирования эксперимента от натурального являются:

1) простота повторения условий эксперимента с моделью на ЭВМ;

2) возможность управления экспериментом (включая его прерывание и возобновление);

3) легкость варьирования условиями проведения эксперимента (воздействие внешней среды);

4) наличие корреляции между полученными значениями в ходе эксперимента;

5) трудности, связанные с определением интервала моделирования (0, Т).

В зависимости от того, какую роль играет каждая переменная в проводимом эксперименте, она может являться либо фактором, либо реакцией. Пусть, например, имеют место две переменные x и y. Тогда, цель эксперимента – изучение влияния переменной x на переменную y, то x – фактор, а y – реакция. Каждый фактор x_i, i= может принимать в эксперименте одно или несколько значений, называемых уровнями.

Существует вполне определенная связь между уровнями факторов и реакцией (откликом) системы, которую можно представить в виде соотношения

Функция ψ_l – функция реакции, которую геометрически можно представить как поверхность реакции и в ходе машинного эксперимента ее необходимо определить.

Факторы подразделяются на:

- управляемые, если его уровни целенаправленно выбираются исследователем в процессе эксперимента;

- наблюдаемые, если его значения наблюдаются и регистрируются;

- изучаемые, если он включен в модель для изучения свойств модели;

- количественные, если его числовые значения влияют на реакцию, в противном случае такие факторы называются качественными;

- фиксированные, если исследуются все интересующие значения фактора.

2.5.2 Полный факторный эксперимент. Широкое применение в планировании эксперимента нашли алгебраические полиномы /3/.

Полным факторным экспериментом (ПФЭ) называется эксперимент, в котором реализуются все возможные сочетания n уровней факторов, каждый из которых варьируется на двух уровнях: верхнем x_i^в и нижнем x_i^н, симметрично расположенных относительно основного уровня x_i⁰. Число этих комбинаций определяет тип ПФЭ. В общем случае при ПФЭ уравнение регрессии представляется в виде полинома, слагаемые которого являются членами ряда Тейлора. Этот ряд является разложением неизвестного уравнения, описывающего исследуемый процесс. При статистической обработке опытных данных коэффициенты разложения в ряд Тейлора оцениваются выборочными коэффициентами уравнения регрессии b₀, b_n, b_n-1,n, b_nn и т.д. Уравнение регрессии, полученное в результате обработки опытных данных, записывается в виде (4).

На практике ограничиваются эффектами не выше второго порядка, а остальными членами разложения пренебрегают. После определения коэффициентов регрессии проводят статистический анализ результатов, конечным этапом которого является проверка адекватности полученного уравнения по критерию минимума суммы результатов отклонений.

Уровни факторов представляют собой границы исследуемой области по данному параметру. Планы первого порядка служат для построения математического описания в виде линейных полиномов (линейных уравнений регрессии)

.

Затем выбирается интервал варьирования по каждой переменной – расстояние по данной оси от центра до экспериментальной точки.

Центр, или основной уровень плана

. (10)

Интервал варьирования

. (11)

На следующем этапе совершают операцию приведения (кодирования) переменных. Она заключается в том, что все координаты центра плана приравниваются к нулю, а интервалы варьирования принимают за 1, что позволяет проводить обработку результатов опытов в стандартной форме, не зависящей от условий задачи.

Безразмерные нормированные факторы дают возможность построить матрицу планирования с нижним и верхним уровнями варьирования +1 и –1, при этом учитываются все возможные комбинации.

Матрица планирования состоит из следующих столбцов: столбцов по каждому фактору, столбцов сочетаний факторов и столбца реакций.

Расчет коэффициентов уравнения проводится по методу наименьших квадратов. Причем, таким образом можно найти коэффициенты не только для линейного уравнения, но и уравнения, содержащего еще один член

.

Член, содержащий произведение факторов, называется взаимодействием. Он показывает, насколько влияние одного фактора зависит от значения другого. Как видно из уравнения, всего факторов 3 и один – взаимодействие. Коэффициент при таком члене определяется из выражения

.

Пример 3. Необходимо построить уравнение регрессии для функции

.

Уровни фактора представляют собой границы исследуемой области по исследуемому технологическому параметру. Для примера таковыми технологическими параметрами является температура исходной этиленгликолевой смеси 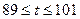⁰С и расхода флегмы кг/ч.

Вводим нижний и верхний уровни параметров:

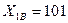⁰С; ⁰С; 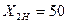кг/ч; кг/ч.

По формуле (10) определяем центр плана, а по формуле (11) - интервал варьирования по оси X. Прибавление интервала варьирования к нулевому уровню дает верхний уровень, а вычитание – нижний. Составляем матрицу планирования (таблица 2.3).

Таблица 2.3 – Матрица планирования эксперимента

№		План ПФЭ	Результат опыта (Yi)	Переменная состояния
опыта			X12
	+1	+1	+1	+1	Y1	1030,44
	+1	+1	-1	–1	Y5	1018,88
	+1	–1	+1	-1	Y6	1114,41
	+1	-1	–1	+1	Y8	1148,58

Х₀ – фиктивный фактор (переменная).

Х₁₂ – переменная взаимовлияния, равная произведению Х₁Х₂.

По формуле

определяем коэффициенты :

Следовательно, искомое уравнение имеет вид

.

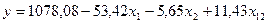Данная формула – это уравнение регрессии для выходной переменной y, которая выражает зависимость величины выходной величины (расхода пара) от 2-х факторов x₁ и x₂ (исходной этиленгликолевой смеси и расхода флегмы) и их взаимовлияния.

Выводы

Особое внимание при формировании расчетно-пояснительной записки курсового проекта уделяется выводам по каждой главе. В выводах формулируются основные итоги, полученные в каждом пункте главы. Таким образом, если глава состоит из трех пунктов, то в выводах должно быть три абзаца с итогами по каждому из них. В общем, выводы оформляются на 0,5 страницы.

Пример4.

В данной главе дано описание технологического процесса как объекта исследования. Представлены основные параметры, переменные и внешние воздействия, подлежащие исследованию. Разработана математическая модель, позволяющая исследователь зависимость качества сусла … от концентрации…

Date: 2016-02-19; view: 861; Нарушение авторских прав