
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Токи в других фазах симметричного трехфазного приёмника могут быть найдены сдвигом по фазе рассчитанного тока ỈAB на 1200 (см. 5.5)
|
|
ỈВС = ỈAB • е – j 120 = 5,2 е j 30 •е – j 120 = 5,2 е – j 90 А;
ỈСА = ỈAB • е j 120 = 5,2 е j 30 •е j 120 = 5,2 е j 150 А.
Линейные токи, подходящие к симметричному треугольнику (ỈA1, ỈВ1 и ỈС1), могут быть определены по первому закону Кирхгофа (см. рис 6.15). Так линейный ток ỈA1 определяется по формуле.
ỈA1 = ỈAB – ỈСА = 5,2 е j 30 – 5,2 е j 150 = 5,2cos(300) + j5,2sin(300) – 5,2cos(1500)
– j5,2sin(1500) = 4,5 + j2,6 + 4,5 – j2,6 = 9ej0 А.
В то же время линейный ток ỈA1 можно рассчитать и по-другому. В симметричной трёхфазной цепи, соединённой в треугольник, линейные токи в  раз больше фазных и сдвинуты относительно их на –300 . Тогда
раз больше фазных и сдвинуты относительно их на –300 . Тогда
ỈA1 =  ỈAB • е – j 30 =
ỈAB • е – j 30 =  • 5,2 е j 30 • е -j 30 = 9ej0 = 9 А.
• 5,2 е j 30 • е -j 30 = 9ej0 = 9 А.
Аналогично можно найти и два других линейных тока (ỈВ1 и ỈС1). Однако в симметричной трехфазной цепи токи всех фаз равны по величине и сдвинуты друг относительно друга на 1200. Поэтому
ỈВ1 = ỈA1 • е – j 120 = 9 е – j 120 = – 4,5 – j 7,8 А;
ỈС1 = ỈA1 • е j 120 = 9 е j 120 = – 4,5 + j7,8 А.
Для несимметричного приёмника, соединённого звездой с нейтральным проводом, комплекс действующего значения фазных токов (ỈA2, ỈВ2 и ỈС2) определяется приложенным к фазе напряжением и сопротивлением фазы.
ỈA2 = ỦА: Z 1 = 300е j 0: 122e –j 35 = 2,46e j 35 = 2,02 + j1,41 A;
ỈB2 = ỦB : Z 2 = 300е – j 120: 100e j 37 = 3 е – j 157 = – 2,76 – j1,17 А;
ỈC2 = ỦC : Z 3 = 300е j 120: 90e j 0 = 3,33 е j 120 = – 1,66 + j2,88 А.
Из-за несимметрии приёмника, соединённого звездой, в нейтральном проводе протекает ток.
İN = İA2 + İB2 + İC2 = 2,02 + j1,41–2,76– j1,17–1,66 + j2,88 = – 2,4 + j3,12=3,9e j127,6
Расчёт фазных токов источника электрической энергии проводим по первому закону Кирхгофа (см. рис. 6.15).
ỈA = ỈA1 + ỈA2 = 9 + 2,02 + j1,41 = 11,02 + j1,41 = 11,11e j 7,3 А;
ỈВ = ỈВ1 + ỈВ2 = – 4,5 – j 7,8 – 2,76 – j1,17 = – 7,26 – j8,97 = 11,54e –j 129 А;
ỈС = ỈС1 + ỈС2 = – 4,5 + j 7,8 – 1,66 + j2,88 = – 6,16 + j10,68 = 12,33e j 120 А.
4. Определим напряжение на всех элементах электрической цепи.
Напряжение на фазах приёмника энергии, соединённого треугольником, равно линейным напряжениям источника энергии.
ỦАB = 520 е j 30 В; ỦВC = 520 е –j 90 В; ỦCA = 520 е j 150 В.
Напряжение на элементах фаз приёмника энергии, соединённого звездой, рассчитаем по закону Ома.
ỦR1 = ỦАa1 = R1 • ỈA2 = 100 • 2,46e j 35 = 246е j 35 В;
ỦC3 =Ủa1N =(– jXC3) • ỈA2 = – j70• 2,46e j 35 = 70е –j 90 • 2,46e j 35 =172,2 е –j 55 В;
ỦR2 = ỦBb1 = R2 • ỈB2 = 80 • 3е – j 157 = 240е – j 157 В;
ỦL2 = Ủb1N = jXL2 • ỈB2 = j60 • 3е – j 157 = 60е j 90 • 3е – j 157 = 180е – j 67 B.
Напряжение на фазе С приёмника энергии в связи с наличием нейтрального провода равно напряжению фазы С источника энергии.
ỦR3 = UCN = ỦC = 300е j 120В.
5. Проверка расчёта по балансу мощности проводится расчётом мощности источника и приёмника энергии и их сопоставлением.
Расчёт активной, реактивной и полной мощности источника электрической энергии может быть проведён с помощью комплекса полной мощности или как сумму мощностей отдельных фаз.
Расчёт активной, реактивной и полной мощности источника электрической энергии проведём с помощью комплекса полной мощности.
S И=  +
+ 
 ,
,
где  ,
,  ,
,  сопряжённые комплексы токов трёхфазного источника, отличающиеся от комплексов действующего значения знаком начальной фазы.
сопряжённые комплексы токов трёхфазного источника, отличающиеся от комплексов действующего значения знаком начальной фазы.
Активная мощность трёхфазного источника энергии равна действительной части комплекса полной мощности PИ = 10420 Вт. Реактивная мощность равна мнимой части комплекса полной мощности QИ =117,21 ВАр. Полная мощность равна модулю комплекса полной мощности SИ = 10421 ВА.
При расчёте мощности источника по отдельным фазам имеем.
Активная мощность фазы А
PA = UA • IA • cos(ΨUA – ΨIA) = 300 • 11,11• cos(00 – 7,30) = 3306 Вт,
где UA и IA – действующее значение напряжения и тока фазы А;
ΨUA и ΨIA – начальные фазынапряжения и тока фазы А.
Реактивная мощность фазы А
QA = UA • IA • sin(ΨUA – ΨIA ) = 300 • 11,11• sin(00 – 7,30) = – 425,5 ВАр.
Полная мощность фазы А
SA = UA • IA = 300 • 11,11= 3333 ВA.
Аналогично рассчитываются активная, реактивная и полная мощности фаз В и С.
PB = UB • IB • cos(ΨUB – ΨIB) = 300•11,54•cos(–1200 – (–1290)) = 3418 Вт,
QB = UB • IB • sin(ΨUB – ΨIB) = 300•11,54• sin(–1200 – (–1290)) = 545,6 ВAр,
SB = UB • IB = 300•11,54 = 3462 ВA,
PC = UC • IC • cos(ΨUC – ΨIC ) = 300 • 12,33• cos(1200 – 1200) = 3698 Вт,
QC = UC • IC • sin(ΨUC – ΨIC ) = 300 • 12,33• sin(1200 – 1200) = 0 ВAр,
SC = UC • IC = 300 • 12,33 = 3699 ВА.
Активная мощность трехфазного источника энергии
P = PA + PВ + PС = 3305 + 3418 + 3698 = 10421 Вт.
Реактивная мощность трехфазного источника энергии
Q = QA + QВ + Q С = – 425,5 + 545,6 + 0 = 117,18 ВАр.
Полная мощность трехфазного источника энергии
S = SA + SВ + S С = 3333 + 3462 + 3699 = 10424 ВА.
В соответствии с балансом мощности мощность приёмников энергии должна быть равна мощности источников энергии электрической цепи.
Комплекс полной мощности приёмников энергии определяется выражением.
S П= ∑(RK ± jXK )  =
= 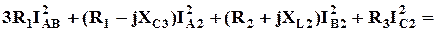

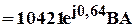 .
.
Сопоставление мощностей источника и приёмника показывает их отличие, которое можно объяснить округлением результатов расчёта на каждом из этапов. Погрешность в расчёте мощностей:
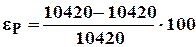 % = 0%,
% = 0%, 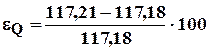 % = 0,02%,
% = 0,02%,
 % = 0%.
% = 0%.
6. Построение потенциальной (топографической) диаграммы напряжений и векторной диаграммы токов рационально начать с потенциальной (топографической) диаграммы напряжений. На диаграмме откладываем векторы всех напряжений в соответствии с их величиной и угловым положением.
ỦА = 300е j 0В; ỦВ = 300е -j120 В; ỦС = 300е j120 В,
ỦАB = 520 е j 30 В; ỦBC = 520 е-j 90 В; ỦCA = 520 е j 150 В;
ỦR1 = ỦАa1 = 246е j 35 В; ỦC3 =Ủa1N = 172,2 е –j 55 В;
ỦR2 = ỦBb1 = 240е – j 157 В; ỦL2 = Ủb1N = 180е – j 67 B.
Обратите внимание на то, что при построении диаграмм для трехфазных цепей оси координат сдвинуты относительно однофазных на 900 против часовой стрелки.
Потенциальная (топографическая) диаграмма напряжений имеет вод
рис. 6.18.

Рис. 6.18. Потенциальная (топографическая) диаграмма напряжений трехфазной цепи
На векторной диаграмме токов откладываем векторы токов в соответствии с их величиной и угловым положением.
ỈAB = 5,2 е j 30 А; ỈВС = 5,2 е – j 90 А; ỈСА = 5,2 е j 150 А;
ỈA1 = 9ej0 А; ỈВ1 = 9 е – j 120 А; ỈС1 = 9 е j 120 А;
ỈA2 = 2,46e j 35 А; ỈB2 = 3 е – j 157 А; ỈC2 = 3,33 е j 120 А;
ỈA = 11,11e j 7,3 А; ỈВ = 11,54e –j 129 А; ỈС = 12,33e j 120 А.
Векторная диаграмма токов электрической цепи представлена на рис 6.19.
 |
Рис. 6.19. Векторная диаграмма токов электрической цепи
Совмещая потенциальную (топографическую) диаграмму напряжений с векторной диаграммой токов, получим общую диаграмму напряжений и токов (рис. 6.20), по которой легко проследить их взаимное расположения (у резисторов напряжение и ток совпадают по фазе, у катушек индуктивности ток отстаёт от напряжения на 900 , а у конденсаторов он опережает напряжение на 900 ).
 |
Рис. 6.20. Потенциальная (топографическая) диаграмма напряжений и векторная диаграмма токов трехфазной электрической цепи
Рассмотрим решение задачи №4 на примере при отсутствии нейтрального провода.
1. Схема замещения электрической цепи. Пусть в таблице 6.9 задано
| Вариант | Z 1 | Z 2 | Z 3 | Z 4 | Нейтраль ный провод |
| ХХ | R1 -j XC3 | R2 + jXL2 | R3 | R1 | нет |
Данным таблицы соответствует схема замещения рис. 6.21.

Рис. 6.21 Схема трёхфазной цепи при отсутствии нейтрального провода
Схема рис. 6.21 отличается от рис. 6.17 только отсутствием нейтрального провода между нейтралью источника (N) и нейтралью приёмника, соединённого звездой (n). При этом наличие или отсутствие нейтрального провода никак не влияет на приёмник, соединённый треугольником. То есть методика расчета приёмника при отсутствии нейтрального провода, соединённого треугольником, будет та же, что и при наличии нейтрального провода. Поэтому для упрощения сохраним те же параметры элементов схемы.
| Вари- ант | Фаза | ЭДС | Нач. фаза | R1 | R2 | R3 | ХL1 | ХL2 | ХL3 | ХC1 | ХC2 | ХC3 |
| В | Градусы | Ом | Ом | Ом | Ом | Ом | Ом | Ом | Ом | Ом | ||
| Х | ЕВ | – 1200 |
2.Тогда, в соответствии с предыдущим расчётом, имеем (см.5.5)
ẺВ = 300е -j120 В.
ẺА = 300е j (-120 + 120) = 300е j 0 В; ẺC = 300е j(-120 – 120) = 300е -j240 = 300е j120 В.
ỦА = 300е j 0В; ỦВ = 300е -j120 В; ỦС = 300е j120 В.
ỦАB =  ỦАе j 30 =
ỦАе j 30 =  •300е j 0 • е j 30 = 520 е j 30 В;
•300е j 0 • е j 30 = 520 е j 30 В;
ỦВC =  ỦBе j 30 =
ỦBе j 30 =  •300е – j 120 • е j 30 = 520 е –j 90 В;
•300е – j 120 • е j 30 = 520 е –j 90 В;
ỦCA =  ỦCе j 30 =
ỦCе j 30 =  •300е j 120 • е j 30 = 520 е j 150 В.
•300е j 120 • е j 30 = 520 е j 150 В.
Сопротивления ветвей электрической цепи, соединённых звездой.
Z 1 = R1 – jXC3 = 100 – j70 = (√1002 + 702 )e j arc tg (– 70 / 100) = 122e –j 35 Ом;
Z 2 = R2 + jXL2 = 80 + j60 = (√802 + 602 )e j arc tg (60 / 80) = 100e j 37 Ом;
Z 3 = R3 = 90 = 90e j 0 Ом.
Сопротивления ветвей электрической цепи, соединённых треугольником.
Z 4 = R1 = 100 = 100e j 0 Ом.
3. Из расчёта токов в ветвях электрической цепи имеем
ỈAB = ỦАB: R1 = 520 е j 30 : 100e j 0 = 5,2 е j 30 А.
ỈВС = ỈAB • е – j 120 = 5,2 е j 30 •е – j 120 = 5,2 е – j 90 А;
ỈСА = ỈAB • е j 120 = 5,2 е j 30 •е j 120 = 5,2 е j 150 А.
ỈA1 = ỈAB – ỈСА = 5,2 е j 30 – 5,2 е j 150 = 5,2cos(300) + j5,2sin(300) – 5,2cos(1500)
– j5,2sin(1500) = 4,5 + j2,6 + 4,5 – j2,6 = 9ej0 А.
ỈВ1 = ỈA1 • е – j 120 = 9 е – j 120 = – 4,5 – j 7,8 А;
ỈС1 = ỈA1 • е j 120 = 9 е j 120 = – 4,5 + j7,8 А.
Для расчёта токов несимметричного приёмника, соединённого звездой без нейтрального провода (ỈA2, ỈВ2 и ỈС2), необходимо определить приложенные к фазам напряжение. Поскольку нейтраль приёмника не соединена с нейтралью источника, то потенциал точки n за счёт несимметрии смещается относительно потенциала точки N. Напряжение смещения определяется формулой.
ŮnN =  ,
,
где проводимости фаз приёмника Y 1 , Y 2 и Y 3 рассчитываются по формулам
 См,
См,
 См,
См,
 См.
См.
Подставляя численные значения, получим величину напряжения смещения.
ŮnN = 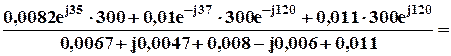
 В.
В.
Напряжения на фазах несимметричного приёмника
Ůan = ŮA – ŮnN = 300 – (– 98,8 +j115,3) = 399,2 – j115,7 = 415,7e–j16 ,
Ůbn = ŮB – ŮnN = –150 – j260 – (– 98,8 +j115,3) = – 50.8 – j375,5 = 378,9e-j97,8 ,
Ůcn = ŮC – ŮnN = –150 + j260 – (– 98,8 +j115,3)= – 50,8 + j144,08 = 152,8ej109,5 .
Фазные токи несимметричного приёмника
İА2 = Y 1 Ůan = 0,0082ej35 415e-j16 = 3,4ej19 = 3,2 +j1,1,
İB2 = Y 2 Ůbn = 0,01e-j37 388,8e-j97,8 = 3,8e-j134,8 = –2,7 – j2,7,
İC2 = Y 3 Ůcn = 0,011ej0 153,5ej109,5 = 1,7ej109,5 = – 0,56 + j1,6.
Расчёт фазных токов источника электрической энергии проводим по первому закону Кирхгофа (см. рис. 6.19).
ỈA = ỈA1 + ỈA2 = 9 + 3,2 + j1,1 = 12,2 + j1,1 = 12,25e j 5,2 А;
ỈВ = ỈВ1 + ỈВ2 = – 4,5 – j 7,8 – 2,7 – j2,7 = – 7,2 – j10,5 = 12e –j 124,4 А;
ỈС = ỈС1 + ỈС2 = – 4,5 + j 7,8 – 0,5 + j1,6 = – 5 + j9,4 = 10,7e j 118 А.
4. Определим напряжение на всех элементах электрической цепи.
Напряжение на фазах приёмника энергии, соединённого треугольником, равно линейным напряжениям источника энергии.
ỦАB = 520 е j 30 В; ỦВC = 520 е –j 90 В; ỦCA = 520 е j 150 В.
Напряжение на элементах фаз приёмника энергии, соединённого звездой, рассчитаем по закону Ома.
ỦR1 = Ủaa1 = R1 • ỈA2 = 100 • 3,4e j 19 = 340,5е j 19 В;
ỦC3 =Ủa1n =(– jXC3) • ỈA2 = – j70• 3,4e j 19 = 70е –j 90 • 3,4e j19 = 238,4 е –j 71 В;
ỦR2 = Ủbb1 = R2 • ỈB2 = 80 • 3,8е – j 134,8 = 303е – j 134,8 В;
ỦL2 = Ủb1n = jXL2 • ỈB2 = j60 • 3,8е – j 134,8 = 60е j 90 • 3,8е – j 134,8 = 227е – j 44,8 B.
Напряжение на фазе c приёмника энергии в связи с отсутствием нейтрального провода равно напряжению Ůcn.
ỦR3 = Ůcn = 152,8ej109,5 В.
5. Проверка расчёта по балансу мощности – это равенство мощностей источника и приёмника энергии. Расчёт активной, реактивной и полной мощности источника электрической энергии проведём с помощью комплекса полной мощности.
S И=  +
+ 
 ,
,
где  ,
,  ,
,  сопряжённые комплексы токов трёхфазного источника, отличающиеся от комплексов действующего значения знаком начальной фазы.
сопряжённые комплексы токов трёхфазного источника, отличающиеся от комплексов действующего значения знаком начальной фазы.
Активная мощность трёхфазного источника энергии равна действительной части комплекса полной мощности PИ = 10637 Вт. Реактивная мощность равна мнимой части комплекса полной мощности QИ =102,2 ВАр. Полная мощность равна модулю комплекса полной мощности SИ = 10638 ВА.
В соответствии с балансом мощности мощность приёмников энергии должна быть равна мощности источников энергии электрической цепи.
Комплекс полной мощности приёмников энергии определяется выражением.
S П= ∑(RK ± jXK )  =
= 

 .
.
Сопоставление мощностей источника и приёмника показывает их отличие, которое можно объяснить округлением результатов расчёта на каждом из этапов. Погрешность в расчёте мощностей:
 % = 0%,
% = 0%,  % = 0,2%,
% = 0,2%,
 % = 0%.
% = 0%.
6. Построение потенциальной (топографической) диаграммы напряжений и векторной диаграммы токов рационально начать с потенциальной (топографической) диаграммы напряжений. На диаграмме откладываем векторы всех напряжений в соответствии с их величиной и угловым положением.
ỦА = 300е j 0 В; ỦВ = 300е -j120 В; ỦС = 300е j120 В,
ỦАB = 520 е j 30 В; ỦBC = 520 е-j 90 В; ỦCA = 520 е j 150 В;
ŮnN = 152,5 ej130,6 B; ỦR1 = ỦАa1 = 340,5е j 19 В; ỦC3 =Ủa1n = 238,4 е –j 71 В;
ỦR2 = ỦВb1 = 303е – j 134,8 В; ỦL2 = Ủb1n = 227е – j 44,8 B;
ỦR3 = ŮСn = 152,8ej109,5 В.
Обратите внимание на то, что при построении диаграмм для трехфазных цепей оси координат сдвинуты относительно однофазных на 900 против часовой стрелки.
Потенциальная (топографическая) диаграмма напряжений имеет вод
рис. 6.22.

Рис. 6.22. Потенциальная (топографическая) диаграмма напряжений
На векторной диаграмме токов откладываем векторы токов в соответствии с их величиной и угловым положением.
ỈAB = 5,2 е j 30 А; ỈВС = 5,2 е – j 90 А; ỈСА = 5,2 е j 150 А;
ỈA1 = 9ej0 А; ỈВ1 = 9 е – j 120 А; ỈС1 = 9 е j 120 А;
İА2 = 3,4ej19 ; İB2 = 3,8e-j134,8 ; İC2 = 1,7ej109,5;
ỈA = 12,25e j 5,2 А; ỈВ = 12e –j 124,4 А; ỈС = 10,7e j 118 А.
Векторная диаграмма токов электрической цепи представлена на рис 6.23.

Рис. 6.23. Векторная диаграмма токов
Совмещая потенциальную (топографическую) диаграмму напряжений с векторной диаграммой токов, получим общую диаграмму напряжений и токов (рис. 6.24), по которой легко проследить их взаимное расположения (у резисторов напряжение и ток совпадают по фазе, у катушек индуктивности ток отстаёт от напряжения на 900 , а у конденсаторов он опережает напряжение на 900 ).

Рис. 6.24. Потенциальная (топографическая) диаграмма напряжений и векторная диаграмма токов
Содержание
| Введение……………………………………………………………... | |
| Программа курса ТОЭ-1…………………………………………… | |
| Перечень лабораторных работ…………………………………….. | |
| Список литературы……………………………………………..…... | |
| Указания по выполнению и оформлению контрольных работ…… | |
| Краткие теоретические сведения ………………………………….. | |
| Контрольные задания……………………………………………….. | |
| Контрольная работа №1……………………………………………... | |
| Контрольная работа №2……………………………………………... |
Date: 2016-02-19; view: 1038; Нарушение авторских прав