
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Методические Указания. Рассмотрим решение задачи № 1 на примере
|
|
Рассмотрим решение задачи № 1 на примере. Пусть в таблице 6.1 задано.
| Вариант | Z1 | Z2 | Z3 | Z4 | Z5 | Зажимы подключения вольтметра | |
| XX | R1 | XL2 | R3 | XC3 | R2 | 4 – 6 |
1. Данным таблицы соответствует схема замещения рис. 6.2.

Рис. 6.2 Схема замещения электрической цепи
Параметры элементов схемы замещения берём из таблицы 6.2.
| Вари- ант | R1 | R2 | R3 | L1 | L2 | L3 | C1 | C2 | C3 | f | Umn |
| Ом | Ом | Ом | mГн | mГн | mГн | мкФ | мкФ | мкФ | Гц | В | |
| Х | 95,54 | 127,4 | 111,5 | 63,7 | 53,1 | U13=90 |
2. Сопротивления элементов схемы замещения.
Для резисторов сопротивления заданы в таблице 6.2.
R1 = 20 Ом; R3 = 30 Ом; R2 = 25 Ом.
Сопротивление катушки индуктивности и конденсатора рассчитываются по формулам (см. 5.4.2).
XL2 = 2πf L2 = 40 Ом; XC3 = 1: 2πf С3 = 60 Ом.
Комплексное сопротивление катушки индуктивности всегда мнимое положительное
Z L2 = j XL2 = j40 = 40е j90 Ом.
Комплексное сопротивление конденсатора также мнимое, но отрицательное
Z C3 = – j XC3 = – j 60 = 60 е - j90 Ом.
3. Для расчёта тока найдём сопротивление Z 13, к которому приложено напряжение U13 (см. 5.8.1).
Z 13 = R1 + j XL2 = 20 + j 40 = 44,72 ej 63,4 Ом,
где 20 + j 40 – алгебраическая (удобная для выполнения математических операций сложения и вычитания) и 44,72 ej 63,4 – показательная (удобная для выполнения математических операций умножения и деления) формы записи сопротивления Z 13 (см. 5.2).
Поскольку начальная фаза напряжения не задана, то примем её равной нулю. То есть комплекс действующего напряжения между точками 1 – 3 (см. 5.3)
Ů13 = 90 ej 0.
По закону Ома (см. 5.7.1) ток, протекающий по R1 и L2:
İ = 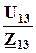 =
=  = 2, 01e – j 63,4 А.
= 2, 01e – j 63,4 А.
При последовательном соединении всех элементов электрической цепи ток во всех её элементах будет один и тот же, т.е.
İ = 2, 01e – j 63,4 А.
4. Используя закон Ома, рассчитаем напряжения на всех элементах электрической цепи и представим их в показательной и алгебраической формах.
Ủ12 = ỦR1 = R1Ỉ = 20 • 2, 01e – j 63,4 = 40,2e – j 63,4 = 18 – j35,9 В;
Ủ23 = ỦL2 = Z L2 Ỉ = 40е j90 • 2, 01e – j 63,4 = 80,4ej 26,6 = 71,9 + j 36 В;
Ủ34 = ỦR3 = R3 Ỉ = 30 • 2, 01e – j 63,4 = 60,3e – j 63,4 = 27 – j53,9 В;
Ủ45 = ỦC3 = Z C3 Ỉ = 60е – j 90 • 2, 01e – j 63,4 = 120,6e – j 153,4 = – 107,8 – j 54 В;
Ủ56 = ỦR2 = R2 Ỉ = 25 • 2, 01e – j 63,4 = 50,25e – j 63,4 = 22,5 – j44,9 В;
5. По второму закону Кирхгофа алгебраическая сумма напряжений на всех пассивных элементах замкнутого контура электрической цепи равна алгебраической сумме ЭДС источников в этом контуре (см. 5.7.2). Поскольку у нас один контур, ток направлен во всех элементах электрической цепи в одном направлении и имеется один источник ЭДС, то её величина будет равна просто сумме напряжений на всех участках цепи. Удобнее суммировать комплексные числа в алгебраической форме. Тогда:
Ẻ = Ủ12 + Ủ23 + Ủ34 + Ủ45 + Ủ56 = 18 – j35,9 + 71,9 + j 36 + 27 – j53,9 – 107,8
– j 54 + 22,5 – j44,9 = 31,6 – j152,7 = 156 е – j 78,3 В.
ЭДС источника в электрической цепи с последовательным соединением элементов может быть также найдена по закону Ома, как произведение суммарного сопротивления цепи на протекающий по ней ток. Суммарное сопротивление электрической цепи (см. 5.9.1):
Z ∑ = R1 + j XL2 + R3 – j XC3 + R2 = 20 + j 40 + 30 – j 60 + 25 = 75 – j 20 =
= 77,62e – j 14,9 Ом.
Тогда Ẻ = Z ∑ Ỉ = 77,62e – j 14,9 • 2, 01e – j 63,4 = 156 е – j 78,3 В.
6. Рассчитаем показание вольтметра, подключённого к точкам 4 – 6. Поскольку вольтметр электромагнитной системы показывает действующее значение напряжения, то оно может быть определено по закону Ома как произведение полного сопротивления участка цепи между точками 4 – 6 на протекающий ток. Полное сопротивление этого участка цепи определяется формулой:
Z 46 =  = 65 Ом.
= 65 Ом.
Действующее значение тока равно I = 2,01 А. Тогда показание вольтметра.
UV = U46 = 65 • 2,01 = 130,65 В.
7. Для построения временных зависимостей e(t) и i(t) перейдём от комплексов действующих значений этих величин к их мгновенным значениям. Амплитуда синусоид в 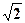 раз больше действующего значения. Найдём амплитуды ЭДС и тока (см. 5.3).
раз больше действующего значения. Найдём амплитуды ЭДС и тока (см. 5.3).
Em = 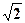 E =
E = 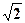 • 156 = 220,6 В; Im =
• 156 = 220,6 В; Im = 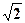 • 2,01 = 2,84 А.
• 2,01 = 2,84 А.
Угловая частота синусоид ω связана с частотой переменного тока f соотношением:
ω = 2πf = 2π • 50 = 314 1/с.
Мгновенные значения ЭДС источника и тока будут изменяться синусоидально во времени в соответствии с формулами.
e(t) = Em sin(ωt + ψe ) = 220,6 sin(314t – 78,30 );
i(t) = Im sin(ωt + ψi ) = 2,84 sin(314t – 63,40 );
где ψe = 78,30 и ψi = 63,40 – начальные фазы ЭДС и тока, рассчитанные ранее для комплексных значений этих величин.
Иногда рационально строить зависимости e(t) и i(t) не в функции времени, а в функции фазы ωt, задаваяеё в пределах периода равной 3600 . При построении графиков с помощью компьютера в некоторых программах следует перевести начальную фазу в радианы.
ψe = –78,30 = – 1,37 р; ψi = – 63,40 = – 1,1 р.
Графики зависимостей e(ωt) и i(ωt) на рис.6.3.
 |
Рис 6.3. Графики изменения мгновенных значений ЭДС и тока
в функции времени.
8. Баланс мощности в электрических цепях заключается в равенстве сумм активной и реактивной мощностей всех источников и приёмников электрической энергии.
∑ РИК = ∑ РПК и ∑ QИК = ∑ QПК,
где ∑ РИК и ∑ QИК –сумма активных и реактивных мощностей всех источников энергии электрической цепи;
∑ РПК и ∑ QПК – сумма активных и реактивных мощностей всех приёмников энергии электрической цепи.
Для источника активная мощность определяется формулой:
РИК = ЕК IK cos(ψek – ψik).
Поскольку в задаче один источник, то его мощность:
РИ = Е I cos(ψe – ψi ) = 156 • 2.01 • cos(– 78,3 – (– 63,4)) = 303 Вт.
Активную мощность потребляют только резисторы, поэтому
∑ РПК = R1 I2 + R3 I2 + R2 I2 = 20 • 2,012 + 30 • 2,012 + 25 • 2,012 = 303 Вт.
Погрешность баланса активной мощности
ΔР = [(│ РИ – ∑ РПК│): (∑ РИК )] • 100% = [ (303 – 303):303] • 100% = 0%.
Реактивная мощность источника определяется формулой
QИ = Е I sin(ψe – ψi ) = 156 • 2.01 • sin(– 78,3 – (– 63,4)) = –80,62 ВAр.
Реактивную мощность потребляют реактивные элементы электрической цепи – катушки индуктивности и конденсаторы. Для к-го реактивного элемента реактивная мощность определяется формулой:
QПК = ХК I2К ,
при этом сопротивление реактивного элемента (ХК )берётся положительным для катушек индуктивности и отрицательным для конденсаторов.
В нашем случае
∑ QПК = XL2 I2 – XC3 I2 = 40 • 2,012 – 60 • 2,012 = – 80,8 ВАр.
Погрешность баланса реактивных мощностей.
ΔQ = (│ QИ – ∑ QПК │• 100%): (∑ QИК ) =│ (–80,62+80,8) │: │ 80,62 │= 0,22%.
Полученные значения погрешностей баланса активных и реактивных мощностей показывают на то, что проведённый ранее расчёт выполнен достаточно точно.
9. Потенциальная (топографическая) диаграмма напряжений – это совокупность точек на комплексной плоскости, каждая из которых соответствует потенциалу точки электрической цепи относительно точки, потенциал которой равен нулю. То есть необходимо принять потенциал одной из точек электрической цепи равным нулю. Выбор этой точки произволен. Однако, если желательно иметь всю диаграмму сориентированной по току, то при расчёте потенциалов надо двигаться против тока. Поэтому в нашей задаче рационально приравнять к нулю потенциал точки 6 (φ6 = 0). Тогда потенциал точки 5 будет выше потенциала точки 6 на величину напряжения на резисторе R2 (ток течёт от большего потенциала к меньшему). То есть
φ 5 = φ6 + ỦR2 = φ6 + R2 I = 0 + 22,5 – j44,9 = 50,25e – j 63,4 В.
Аналогично потенциал точки 4 будет выше потенциала точки 5 на величину напряжения на конденсаторе С3.
φ 4 = φ5 + ỦC3 = φ5 + Z C3 Ỉ = 22,5 – j44,9 – 107,8 – j 54 =
= – 85,3 – j 98,9 = 130,6e – j 130,8 В.
Расчёт потенциалов остальных точек электрической цепи аналогичен.
φ 3 = φ4 + ỦR3 = φ4 + R3 I = – 85,3 – j 98,9 + 27 – j53,9 =
= – 58,3 – j 152,8 = 163,5 e – j 110,9 В.
φ 2 = φ3 + ỦL2 = φ3 + Z L2 Ỉ = – 58,3 – j 152,8 + 71,9 + j 36 =
= 13,6 – j 116,8 = 117,6e – j 83,4 В.
φ 1 = φ2 + ỦR1 = φ2 + R1 I = 13,6 – j 116,8 + 18 – j35,9 =
= 31,6 – j 152,7 = 156 e – j 78,3 В.
Обратите внимание на то, что потенциал точки 1 (φ 1 ) совпал с величиной ЭДС источника, создающей напряжение Ủ16 .
Потенциальную диаграмму можно строить и не рассчитывая потенциалы всех точек. Для этого необходимо к потенциалу предыдущей точки прибавлять в масштабе отрезок, соответствующий комплексному значению напряжения на последующем элементе схемы электрической цепи. То есть
φ 5 = φ6 + ỦR2 ;
φ 4 = φ5 + ỦC3 ;
φ 3 = φ4 + ỦR3 ;
φ 2 = φ3 + ỦL2 ;
R1.
При этом желательно сначала построить на комплексной плоскости в своём масштабе вектор тока и затем откладывать отрезки, пропорциональные напряжениям на элементах электрической цепи, с учётом их сдвига относительно тока (напряжение на резисторе совпадает по фазе с током, напряжение на катушке индуктивности опережает ток по фазе на 900 , напряжение на конденсаторе отстаёт от тока по фазе на 900 ).
Векторная диаграмма тока и потенциальная диаграмма напряжений электрической цепи представлены на рис. 6.4.

Рис 6.4. Векторная диаграмма тока и потенциальная диаграмма
напряжений электрической цепи
Удобство потенциальной диаграммы в том, что с помощью её можно определить напряжение между любыми двумя точками электрической цепи. Например, измерив отрезок между точками 4 и 6 можно, использовав масштаб, определить напряжение на зажимах вольтметра V.
Задача №2.
К электрической цепи (рис. 6.5) приложено несинусоидальное напряжение, представленное в виде гармонического ряда:
u(t) = U0 + Um1 sin(ωt + ΨU1) + Um3 sin(3ωt + ΨU3 ).
Параметры этого напряжения даны в таблице 6.3 (вариант выбирается по последней цифре шифра).
Таблица 6.3. Параметры несинусоидального напряжения u(t).
| Вари- ант | U0 | Um1 | Um3 | ΨU1 | ΨU3 | f(1) |
| В | В | В | Градусы | Градусы | Гц | |
| 200 | 450 | |||||
| 300 | 150 | |||||
| 100 | 700 | |||||
| 400 | 200 | |||||
| 600 | 350 | |||||
| 250 | 750 | |||||
| 150 | 200 | |||||
| 350 | 900 | |||||
| 00 | 550 | |||||
| 750 | 250 |
Здесь f(1) – частота первой гармоники напряжения.
Требуется
1. записать выражение для приложенного к электрической цепи напряжения в соответствии с данными табл. 6.3.
2. в соответствии с табл. 6.4 нарисовать схему замещения (вариант выбирается по последним цифрам зачетки);
3. по данным табл. 6.5 (вариант выбирается по последним цифрам зачетки) определить сопротивления пассивных двухполюсников П1, П2 и П3 электрической цепи для каждой из гармоник;
4. рассчитать комплексные сопротивления всех ветвей электрической цепи для каждой из гармоник;
5. по заданному напряжению и сопротивлению элементов рассчитать мгновенные значения токов во всех ветвях i1 (t), i2 (t), i3 (t) и общий ток i(t);
6. построить графики мгновенных значений напряжения u(t) и тока i(t);
7. рассчитать показания амперметра и вольтметра электромагнитной системы и ваттметра электродинамической системы.
Примечание: по указанию преподавателя для некоторых специальностей расчёт может проводиться при уменьшенном гармоническом ряде входного напряжения (например, только для первой гармоники).

Рис. 6.5. Схема электрической цепи
Таблица 6.4. Вариант вида пассивных двухполюсников электрической цепи
| Вариант | П1 | П2 | П3 | |
| R1 + jXL1 | R2 | -j XC2 | ||
| R1 - j XC2 | jXL3 + R3 | -j XC1 | ||
| -j XC2 | R1 - j XC1 | jXL3 + R2 | ||
| R1 + j XL1 | - jXC3 | R3 | ||
| R3 + j XL1 | -j XC3 | R1 - jXC2 | ||
| R2 - j XC2 | jXL3 +R1 | -j XC1 | ||
| -j XC1 | R1 - j XC2 | jXL3 + R3 | ||
| jXL2 + R3 | -jXC1 + R1 | -j XC2 | ||
| R1 + j XL3 | - jXC1 | R3 -j XC2 | ||
| R3 - j XC1 | R1 -j XC2 | R2+ jXL2 | ||
| R2 + j XL3 | R1 - jXC3 | -j XC1 | ||
| R1 | - jXC2 | R2 + j XL1 | ||
| jXL1 + R3 | -j XC1 | - jXC3 + R2 | ||
| - jXC1 + R1 | R3 -j XC2 | R2+ jXL2 | ||
| -j XC3 | R2 - jХC2 | R3 + j XL3 | ||
| R3 + j XL1 | - jXC1 + R1 | -j XC2 | ||
| -j XC2 | jXL2 + R1 | R3 - j XC3 | ||
| R3 - jXC1 | R2 -j XC3 | R1 + jXL2 | ||
| R3 + j XL2 | R1 - jXC3 | -j XC2 | ||
| R1 -j XC2 | R2 - jXC3 | R3 + j XL1 | ||
| R3 - j XC1 | -j XC3 | R2 + jXL3 | ||
| R2 + j XL1 | - jXC2 + R1 | R3 -j XC2 | ||
| -j XC2 | R2 + j XL2 | - jXC3 + R3 | ||
| R3 - jXC3 | R1 | R2 + j XL2 | ||
| R2 - j XC2 | R3 -j XC1 | jXL1 + R1 | ||
| -j XC1 | R2 + jXL1 | R1 - j XC3 | ||
| R3 + jXL2 | R1 -j XC2 | R2 - jXC1 | ||
| R3 - j XC3 | R1 + jXL3 | -j XC2 | ||
| -j XC3 | R1 - j XC1 | R3 + jXL2 | ||
| R2 + j XL3 | - jXC1 + R3 | R1 -j XC2 | ||
| R3 + j XL3 | R2 +j XL2 | R1 - jXC2 | ||
| -j XC2 | R2 + jXL1 | R3 - j XC2 | ||
| - jXC2 + R2 | R3 -j XC1 | jXL3 + R1 | ||
| R1 - jXC1 | R2 + j XL2 | R3 +j XL1 | ||
| -j XC1 | R3 - jXC3 | R2 + j XL1 | ||
| R3 - jXC2 | R1 -j XC1 | R2 + jXL3 | ||
| R2 + j XL3 | R1 - jXC2 | R3 -j XC3 | ||
| R3 | R2 - jXC1 | jXL1 + R1 | ||
| R1 -jXC2 | -j XC2 | R3 + j XL2 | ||
| R3 -j XC2 | R2 - j XC3 | R1 + jXL3 | ||
| - j XC2 + R2 | R3 + jXL1 | R1 +j XL2 | ||
| jXL3 + R3 | R2 | R1 - j XC1 | ||
| R3 - j XC3 | jXL2 + R1 | -j XC1 | ||
| R1 +j XL3 | R3 - j XC2 | R2 + jXL1 | ||
| R3 + j XL1 | -jXC3 + R2 | R1 | ||
| jXL3 + R2 | -j XC3 | R1 - jXC2 | ||
| R1 -j XC3 | jXL1 + R3 | -j XC2 + R2 | ||
| R2 - jXC3 | R1 +j XL2 | R2 + jXL1 | ||
| -jXC2 + R1 | R2 + j XL3 | -j XC2 | ||
| R3 -j XC2 | R1 - jXC1 | R2 + j XL2 | ||
| R1 - j XC1 | R3 | R2 + jXL3 | ||
| R3 + j XL3 | -jXC2 + R1 | R2 +j XL2 | ||
| -j XC3 | R3 - jXC1 | R1 + j XL2 | ||
| R2 -j XC2 | - jXC3 + R3 | R1 + j XL1 | ||
| R3 + j XL3 | R2 -j XL2 | R1 - jXC2 | ||
| - jXC1 + R2 | R1 + j XL2 | R3 | ||
| -j XC2 | R1 - j XC1 | jXL3 + R2 | ||
| R2 -j XC2 | jXL2 + R1 | R3 - j XC3 | ||
| jXL1 + R2 | R1 +j XL2 | - jXC2 + R3 | ||
| R1 + j XL1 | R3 - jXC3 | R2 | ||
| R1 - jXC2 | -j XC1 | R3 + jXL3 | ||
| R3 +j XL2 | R2 + jXL1 | R1 - j XC2 | ||
| R3 + jXL3 | R1 | - jXC1 + R2 | ||
| R3 - j XC3 | -j XC2 | R1 + jXL2 | ||
| R2 -j XC2 | R3 + jXL1 | R1 - j XC2 | ||
| R1 + jXL3 | R2 -j XL2 | -jXC1 + R1 | ||
| R3 - j XC3 | R1 + jXL2 | -j XC3 | ||
| jXL1 + R3 | R3 | R2 - jXC2 | ||
| R3 -j XC2 | jXL3 + R2 | - jXC1 + R1 | ||
| R3 - jXC1 | R2 +j XL2 | R1 + jXL3 | ||
| R1 + j XL2 | -jXC1 + R3 | R2 | ||
| R1 + jXL1 | -j XC2 | R3 - jXC3 | ||
| - jXC3 + R2 | R1 + jXL2 | R3 -j XC2 | ||
| R3 +j XL2 | R1 - jXC2 | R2 + jXL1 | ||
| R1 + j XL1 | - jXC3 + R2 | R3 | ||
| R3 + j XL3 | R2 -j XC1 | R1 - jXC2 | ||
| R2 | R1 - j XC2 | R3 + jXL1 | ||
| R3 + j XL1 | - jXC3 + R1 | -j XC3 | ||
| R1-j XC3 | R3 + j XL3 | R2 - jXC2 | ||
| R3 -j XL1 | R2 - jXC1 | R1 +jXL2 | ||
| R2 + j XL1 | R3 | R1 - jXC3 | ||
| R1 + j XL3 | - jXC2 + R3 | -j XC1 | ||
| R1 - j XC2 | R2 -j XL2 | R3 + jXL1 | ||
| R2 -j XC3 | R1 + jXL3 | R3 - j XC1 | ||
| R1 + jXL1 | -j XC2 | - jXC2 + R2 | ||
| R1 | R2 - jXC3 | R3 + j XL1 | ||
| R2 - jXC2 | R3 -j XC1 | jXL3 + R1 | ||
| - jXC2 + R2 | R3 + jXL1 | -j XC3 | ||
| R3 + jXL1 | R2 -j XL2 | R1 - jXC3 | ||
| R2 - jXC2 | R3 -j XC3 | R1 + jXL3 | ||
| R1 | R2 + jXL1 | R3 - j XC2 | ||
| R1 + jXL3 | R3 -j XC2 | - jXC1 + R1 | ||
| R2 - j XC3 | R1 + jXL2 | R3 +j XL3 | ||
| jXL1 + R2 | -j XC2 | R3 - jXC2 | ||
| R1 -j XC2 | R3 + jXL3 | - jXC1 + R2 | ||
| R2 | R3 - j XC3 | R1 + jXL2 | ||
| R3 + j XL2 | - jXC1 + R2 | R1 -j XC2 | ||
| -j XC2 | R2 - jXC3 | R3 +j XL1 | ||
| R1 - jXC2 | R3 +j XL1 | R2 + jXL3 | ||
| R2 -j XC3 | R3 + jXL1 | R1 - j XC1 |
Таблица 6.5. Параметры элементов электрической цепи
| Вари- ант | R1 | R2 | R3 | L1 | L2 | L3 | C1 | C2 | C3 |
| Ом | Ом | Ом | mГн | mГн | mГн | мкФ | мкФ | мкФ | |
| 127,4 | 95,54 | 111,5 | 106,2 | 79,6 | 113,7 | ||||
| 132,6 | 145,9 | 159,2 | 55,26 | 53,05 | 42,78 | ||||
| 103,5 | 111,4 | 95,5 | 30,04 | 25,28 | 35,39 | ||||
| 63,7 | 74,3 | 79,6 | 17,12 | 25,89 | 37,91 | ||||
| 55,7 | 59,7 | 47,7 | 12,44 | 15,02 | 13,97 | ||||
| 23,87 | 27,85 | 31,83 | 8,85 | 7,11 | 5,85 | ||||
| 25,46 | 27,06 | 28,65 | 4,14 | 5,14 | 4,08 | ||||
| 137,9 | 148,5 | 169,8 | 63,66 | 42,45 | 11,83 | ||||
| 76,39 | 89,13 | 114,6 | 28,3 | 24,5 | 33,52 | ||||
| 57,3 | 63,66 | 70,03 | 7,08 | 8,17 | 10,27 |
Date: 2016-02-19; view: 557; Нарушение авторских прав