
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Методические Указания. Рассмотрим решение задачи № 3 на двух примерах
|
|
Рассмотрим решение задачи № 3 на двух примерах.
Пример 1. Пусть в таблице 6.7 задано.
| Вариант | Z 1 Ом | Z 2 Ом | Z 3 Ом | Режим работы | Коэфф связи КС | Катушки с индуктивной связью |
| Х1 | R3 +jXL1 | R2 +jXL2 | R1 +jXL3 | кз | 0,65 | L1 – L2 |
1. Данным таблицы соответствует схема замещения рис. 6.9.

Рис. 6.9. Схема замещения электрической цепи
2. Пусть в таблице 6.8 параметры элементов схемы имеют следующее значение.
| Вари- ант | R1 | R2 | R3 | L1 | L2 | L3 | C1 | C2 | C3 | f | U1 |
| Ом | Ом | Ом | mГн | mГн | mГн | мкФ | мкФ | мкФ | Гц | В | |
| Х | 95,54 | 127,4 | 111,5 | 63,7 | 53,1 |
Для расчета параметров четырёхполюсника необходимо определить сопротивления всех элементов схемы.
Для резисторов сопротивления заданы в таблице 6.8.
R1 = 20 Ом; R2 = 25 Ом; R3 = 30 Ом.
Сопротивление катушек индуктивности рассчитываются по формулам.
XL1 = 2πf L1 = 60 Ом; XL2 = 2πf L2 = 80 Ом; XL3 = 2πf L3 = 70 Ом;
Комплексное сопротивление ветвей электрической цепи.
Z 1 = R1 + jXL1 = 20 + j60 = 63,25e j 71,6 Ом;
Z 2 = R2 + jXL2 = 25 + j80 = 83,8e j 72,6 Ом;
Z 3 = R3 + jXL3 = 30 + j70 = 76,16e j 66,8 Ом;
Коэффициент взаимоиндукции M определяется через заданный коэффициент связи KC и индуктивности магнитно связанных катушек L1 и L2 по формуле.
M = KC •  = 0,65•
= 0,65• 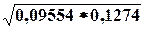 = 0,07171 Гн = 71,71 mГн.
= 0,07171 Гн = 71,71 mГн.
Сопротивление взаимоиндукции XM определяется выражением.
XM = 2πf M = 45 Ом.
3. Связь между напряжениями и токами пассивного четырёхполюсника определяется следующей системой уравнений.
Ủ1 = A Ủ2 + B Ỉ2 . (6.1)
Ỉ1 = C Ủ2 + D Ỉ2 . (6.2)
Параметры A, B, C, D рассчитаем с помощью законов Кирхгофа.
По первому закону Кирхгофа для электрической цепи рис. 6.9.
Ỉ1 = Ỉ2 + Ỉ3 .
Для определения тока Ỉ3 найдём напряжение между точками 6 и 2 с учётом взаимоиндуктивности катушек L1 и L2 ( см.5.4.3).
Ủ62 = Z 2 • Ỉ3 + j XM • Ỉ1  Ỉ3 = (Ủ62 – j XM • Ỉ1): Z 2 .
Ỉ3 = (Ủ62 – j XM • Ỉ1): Z 2 .
Напряжение Ủ62 можно найти, пройдя от точки 6 к точке 2 по другой ветви.
Ủ62 = Z 3 • Ỉ2 + Ủ2 .
Подставив его значение в предыдущую формулу, получим выражение для тока Ỉ3 .
Ỉ3 = (Z 3 • Ỉ2 + Ủ2 – j XM • Ỉ1): Z 2 (6.3)
и после преобразований для тока Ỉ1 .
Ỉ1 =  Ủ2 +
Ủ2 + 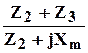 Ỉ2 . (6.4)
Ỉ2 . (6.4)
Сопоставляя уравнения (2) и (4) можно видеть, что коэффициенты C и D соответственно определяются выражениями.
C =  =
=  = 0,007845e – j78,69 См;
= 0,007845e – j78,69 См;
D = 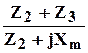 =
=  =
=  =
=  = 1,2533e – j8,83 .
= 1,2533e – j8,83 .
Для нахождения параметров A и B составим уравнения по второму закону Кирхгофа для контура Ủ1 → Z 1 → Z 3 → Ủ2 .
Ủ1 = Z 1 • Ỉ1 + j XM • Ỉ3 + Z 3 • Ỉ2 + Ủ2
Подставив в это уравнение выражения для Ỉ3 (6.3) и для Ỉ1 (6.4) после преобразований окончательно получим.
Ủ1 =  Ủ2 +
Ủ2 +  Ỉ2 .
Ỉ2 .
Таким образом, сопоставляя полученное выражение с уравнением (6.1), можно рассчитать коэффициенты A и B.
A =  =
=  =
=  =
=  =
=
=1,494e-j2,39 ;
B =  =
=
=  =
=
 =
=  =
=
=  = 168,74ej63,61 Ом.
= 168,74ej63,61 Ом.
Проверку правильности расчёта коэффициентов A,B,C,D сделаем по уравнению, которое справедливо для любого пассивного четырёхполюсника.
A • D – B • C = 1.
 •
•  –
–  •
• 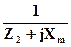 = 1
= 1
4. Рассчитаем токи в рассматриваемой электрической цепи в режиме короткого замыкания (см. табл. 6.7). Схема в этом случае имеет вид рис. 6.10.
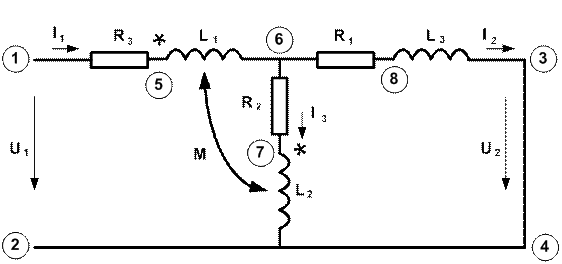
Рис. 6.10. Схема электрической цепи в режиме короткого замыкания
Поскольку выходные зажимы четырехполюсника 3 и 4 замкнуты накоротко, то напряжение Ủ2 равно нулю, и уравнения (6.1) и (6.2) приобретают вид.
Ủ1 = B Ỉ2 . (6.5)
Ỉ1 = D Ỉ2 . (6.6 )
Из уравнения (6.5) может быть определён ток Ỉ2 . При этом примем начальную фазу напряжения Ủ1 равной нулю.
Ỉ2 = Ủ1 : B = 90e j 0 : 168,74 j 63,61 = 0,53 e -j 63,61 А.
Из уравнения (6.6) находим Ỉ1 .
Ỉ1 = D Ỉ2 = 1,253e – j8,89 • 0,53 e -j 63,61 = 0,664e -j 72,5 А.
Из первого закона Кирхгофа для узла 6 найдём ток Ỉ3 .
Ỉ3 = Ỉ1 – Ỉ2 = 0,664e -j 72,5 – 0,53 e -j 63,61 = – 0,0359 – j0,1585 = 0,1625e –j 102,8 А.
5. Для построения потенциальной диаграммы рассчитаем напряжения на элементах электрической цепи.
Ủ15 = ỦR1= R1 • Ỉ1 = 20 • 0,664e -j 72,5= 13,28e -j 72,5 B.
При расчете напряжения на катушке L1 учтём не только падение напряжения от тока Ỉ1 , но и напряжение, наводимое через взаимоиндуктивность от тока Ỉ3 .
Ủ56 = ỦL1= jXL1 • Ỉ1 + jXM • Ỉ3 = 60e j 90 • 0,664e -j 72,5 + 45 e j 90 • 0,1625e –j 102,8 =
= 39,84e j 17,5 + 7,31e –j 12,8 = 45,1 +j10,36 = 46,28 e j 12,94 B.
Остальные напряжения рассчитаем аналогично.
Ủ67 = ỦR2= R2 • Ỉ3 = 25 • 0,1625e –j 102,8 = 4,06 e –j 102,8 B;
Ủ72 = ỦL2= jXL2 • Ỉ3 + jXM • Ỉ1 = 80e j 90 • 0,1625e –j 102,8 + 45e j 90 • 0,664e -j 72,5=
= 13e –j 12,8 + 29,88e j 17,5 = 41,17 +j6,1= 41,62e j 11,54 B.
Ủ68 = ỦR3= R3 • Ỉ2 = 3 0 • 0,53 e -j 63,61 = 15,9 e -j 63,61 B.
Ủ82 = ỦL3= jXL3 • Ỉ2 = 70e j 90 • 0,53 e -j 63,61 = 37,1 e j 26,39 B.
 При построении потенциальной диаграммы примем потенциал точки 2 равным нулю (φ2 = 0).
При построении потенциальной диаграммы примем потенциал точки 2 равным нулю (φ2 = 0).
Рис. 6.8. Векторная диаграмма токов и потенциальная диаграмма напряжений электрической цепи
6. расчёт параметров активного двухполюсника, эквивалентного четырёхполюснику, проведём методом холостого хода и короткого замыкания.
При холостом ходе уравнение (6.1) имеет вид.
Ủ1ХХ = A Ủ2ХХ.
Тогда, приняв напряжение Ủ1ХХ =Ủ1 = 90 В и зная рассчитанное значение А = 1,494e-j2,39 , имеем
Ủ2ХХ =  В.
В.
При коротком замыкании уравнение (6.1) имеет вид.
Ủ1КЗ = B Ỉ2КЗ .
При том же напряжении на входе электрической цепи и при рассчитанном значении В = 168,74 j 63,61 Ом имеем.
Ỉ2КЗ =  А.
А.
Внутреннее сопротивление активного двухполюсника (эквивалентного генератора) определяем как отношение напряжение холостого хода на зажимах двухполюсника к току его короткого замыкания.
Z ВН =  Ом.
Ом.
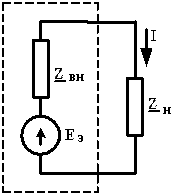
Схема активного двухполюсника с подключённым приёмником энергии Z Н представлена на рис.6.11, где эквивалентная ЭДС двухполюсника
ẺЭ = Ủ2ХХ = 60,24ej2,39
При согласованной нагрузке сопротивление приёмника энергии Z Н равно внутреннему сопротивлению активного двухполюсника Z ВН ( см.5.8.6). То есть
Z Н = Z ВН = 113,66ej66 Ом.
Рис 6.11. Схема активного двухполюсника с приёмником энергии
Тогда ток приёмника энергии определяется по формуле.
Ỉ =  A.
A.
Пример 2. Рассмотрим другой метод определения A, B, C, D параметровчетырёхполюсника. Пусть в таблице 6.7 задано.
| Вариант | Z 1 Ом | Z 2 Ом | Z 3 Ом | Режим работы | Коэфф связи КС | Катушки с индуктивной связью |
| Х2 | R3 +jXL1 | R2 +jXL2 | R1 +jXL3 | хх | 0,65 | L1 – L2 |
1.
 |
Данным таблицы соответствует схема замещения рис. 6.12.
Рис. 6.12. Схема замещения электрической цепи
2. Пусть в таблице 6.8 параметры элементов схемы имеют то же значение, что и в примере 1.
| Вари- ант | R1 | R2 | R3 | L1 | L2 | L3 | C1 | C2 | C3 | f | U1 |
| Ом | Ом | Ом | mГн | mГн | mГн | мкФ | мкФ | мкФ | Гц | В | |
| Х | 95,54 | 127,4 | 111,5 | 63,7 | 53,1 |
Для расчета параметров четырёхполюсника определим сопротивления всех элементов схемы.
Для резисторов сопротивления заданы в таблице 6.8.
R1 = 20 Ом; R2 = 25 Ом; R3 = 30 Ом.
Сопротивление катушек индуктивности рассчитываются по формулам.
XL1 = 2πf L1 = 60 Ом; XL2 = 2πf L2 = 80 Ом; XL3 = 2πf L3 = 70 Ом;
Комплексное сопротивление ветвей электрической цепи.
Z 1 = R1 + jXL1 = 20 + j60 = 63,25e j 71,6 Ом;
Z 2 = R2 + jXL2 = 25 + j80 = 83,8e j 72,6 Ом;
Z 3 = R3 + jXL3 = 30 + j70 = 76,16e j 66,8 Ом;
Коэффициент взаимоиндукции M определяется через заданный коэффициент связи KC и индуктивности магнитно-связанных катушек L1 и L2 по формуле (см. 5.4.3).
M = KC •  = 0,65 •
= 0,65 •  = 0,07171 Гн = 71,71 mГн.
= 0,07171 Гн = 71,71 mГн.
Сопротивление взаимоиндукции XM определяется выражением.
XM = 2πf M = 45 Ом.
3. Связь между напряжениями и токами пассивного четырёхполюсника определяется уже рассмотренной системой уравнений (см. 5.4.4).
Ủ1 = A Ủ2 + B Ỉ2 . (6.1)
Ỉ1 = C Ủ2 + D Ỉ2 . (6.2)
Параметры A, B, C, D рассчитаем методом холостого хода и короткого замыкания.
При холостом ходе четырёхполюсника ток Ỉ2ХХ = 0. Тогда уравнения (6.1) и (6.2) примут вид.
Ủ1ХХ = A Ủ2ХХ; (6.7)
Ỉ1ХХ = C Ủ2ХХ . (6.8 )
Из них можно найти коэффициенты А и С.
А = Ủ1ХХ: Ủ2ХХ ; С = Ỉ1ХХ : Ủ2ХХ
Поскольку в схеме электрической цепи (рис. 6.9) к зажимам 3 и 4 в режиме холостого хода нагрузка не подключена, то I3ХХ = I5ХХ . В связи с этим по второму закону Кирхгофа имеем.
Ủ1ХХ = Z 2 • Ỉ3ХХ – j XM • Ỉ4ХХ + Z 3 • Ỉ5ХХ = (Z 2 + Z 3 ) • Ỉ3ХХ – j XM • Ỉ4ХХ ;
Ủ1ХХ = Z 1 • Ỉ4ХХ – j XM • Ỉ3ХХ .
В этих уравнениях знак минус перед j XM указывает навстречное действие индуктивно связанных катушек.
Решая полученные уравнения относительно токов Ỉ3ХХ и Ỉ4ХХ, имеем.
Ỉ3ХХ =  ; (6.9)
; (6.9)
Ỉ4ХХ =  . (6.10)
. (6.10)
Напряжение на выходе четырёхполюсника
Ủ2ХХ = Z 3 • Ỉ3ХХ =  .
.
Отсюда находим коэффициент А четырёхполюсника.
А = Ủ1ХХ: Ủ2ХХ =  = 1,1325e –j12,98.
= 1,1325e –j12,98.
По первому закону Кирхгофа определим ток Ỉ1ХХ на входе четырёхполюсника.
Ỉ1ХХ = Ỉ3ХХ + Ỉ4ХХ =  . (6.11)
. (6.11)
С учётом известного Ủ2ХХ находим коэффициент С четырёхполюсника.
С = Ỉ1ХХ : Ủ2ХХ =  = 0,03799e –j70,06 См.
= 0,03799e –j70,06 См.
Для расчёта коэффициентов В и D рассмотрим режим короткого замыкания четырёхполюсника. Схема в этом случае приобретает вид рис. 6.13.
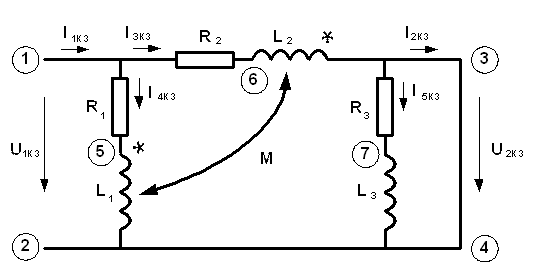 |
Рис. 6.13. Схема электрической цепи в режиме короткого замыкания
Очевидно, что в этом режиме Ủ2КЗ = 0 и I5КЗ = 0. Поэтому Ỉ2КЗ = Ỉ3КЗ, и уравнения четырёхполюсника принимают вид.
Ủ1КЗ = B Ỉ2КЗ; (6.12)
Ỉ1КЗ = D Ỉ2КЗ . (6.13 )
Из этих уравнений легко находятся коэффициенты B и D.
B = Ủ1КЗ : Ỉ2КЗ ; D = Ỉ1КЗ : Ỉ2КЗ .
По схеме в режиме короткого замыкания напряжение Ủ1КЗ приложено к ветвям Z 1 и Z 1 . С учётом взаимоиндуктивности уравнения для этих ветвей имеют вид.
Ủ1КЗ = Z 1 • Ỉ4КЗ – j XM • Ỉ2КЗ ; (6.14)
Ủ1КЗ = Z 2 • Ỉ2КЗ – j XM • Ỉ4КЗ . (6.15)
Решив эту систему уравнений относительно Ỉ2КЗ, имеем.
Ỉ2КЗ =  U1КЗ .
U1КЗ .
Отсюда находим коэффициент В четырёхполюсника.
B = Ủ1КЗ : Ỉ2КЗ =  = 35,97ej47,04 Oм.
= 35,97ej47,04 Oм.
Из уравнений (14) и (15) найдём Ỉ4КЗ .
Ỉ4КЗ = 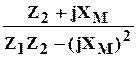 U1КЗ .
U1КЗ .
По первому закону Кирхгофа
Ỉ1КЗ = Ỉ2КЗ + Ỉ4КЗ =  U1КЗ .
U1КЗ .
Отсюда коэффициент D четырёхполюсника
D = Ỉ1КЗ : Ỉ2КЗ =  = 1,781e –j2,92
= 1,781e –j2,92
Проверка правильности расчёта коэффициентов проводится по уравнению
A • D – B • C = 1.
 •
•  –
–  •
• 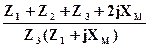 = 1
= 1
4. Для расчёта токов в режиме холостого хода в соответствии с заданием можно использовать выведенные ранее выражения для них (9), (10), (11). Предварительно задавшись начальной фазой напряжения, равной нулю, имеем
Ỉ3ХХ =  =
=  = 1,117e-j53,82 A;
= 1,117e-j53,82 A;
В связи с отсутствием нагрузки на зажимах четырёхполюсника Ỉ5ХХ = Ỉ3ХХ.
Ỉ4ХХ = 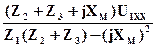 =
=  = 2,117e –j58,79 A;
= 2,117e –j58,79 A;
Ỉ1ХХ =  =
=  = 3,23e –j57,08 A.
= 3,23e –j57,08 A.
5. Для построения потенциальной диаграммы рассчитаем напряжения на отдельных элементах схемы электрической цепи.
Ủ72 = j XL3 • Ỉ5ХХ = 70ej90 • 1,117e-j53,82 = 78,19e j36,18 В;
Ủ37 = R3 • Ỉ5ХХ = 30 • 1,117e-j53,82 = 33,51e -j53,82 В;
Ủ63 = j XL2 • Ỉ3ХХ – j XМ • Ỉ4ХХ = 80ej90 • 1,117e-j53,82 – 45ej90 • 2,117e –j58,79 =
= 89,36e j36,18 – 95,265e j31,21 = – 9,35 + j3,39 = 9,95e j160?07 В;
Ủ16 = R2 • Ỉ3ХХ = 25 • 1,117e-j53,82 = 27,925e -j53,82 В;
Ủ52 = j XL1 • Ỉ4ХХ – j XМ • Ỉ3ХХ = 60ej90 • 2,117e –j58,79 – 45ej90 • 1,117e-j53,82 =
= 127,02e j31,21 – 50,265e j36,18 = 68,06 +j36,15 = 77,06e j27,98 В;
Ủ15 = R1 • Ỉ4ХХ = 20 • 2,117e –j58,79 = 42,34 e –j58,79 В.
 При построении потенциальной диаграммы примем потенциал точки 2 равным нулю (φ2 = 0). Векторная диаграмма токов и потенциальная диаграмма напряжений представлены на рис. 6.14.
При построении потенциальной диаграммы примем потенциал точки 2 равным нулю (φ2 = 0). Векторная диаграмма токов и потенциальная диаграмма напряжений представлены на рис. 6.14.
Рис. 6.14. Векторная диаграмма токов и потенциальная диаграмма
напряжений
6. расчёт параметров активного двухполюсника, эквивалентного четырёхполюснику, проведём методом холостого хода и короткого замыкания.
При холостом ходе уравнение (6.1) имеет вид.
Ủ1ХХ = A Ủ2ХХ.
Тогда, приняв напряжение Ủ1ХХ =Ủ1 = 90 В и зная рассчитанное значение А = 1,1325e-j12,98 , имеем
Ủ2ХХ = 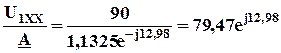 В.
В.
При коротком замыкании уравнение (6.1) имеет вид.
Ủ1КЗ = B Ỉ2КЗ .
При том же напряжении на входе электрической цепи и при рассчитанном значении В = 35,97 j 47,84 Ом имеем.
Ỉ2КЗ =  А.
А.
Внутреннее сопротивление активного двухполюсника (эквивалентного генератора) определяем как отношение напряжение холостого хода на зажимах двухполюсника к току его короткого замыкания.
Z ВН =  Ом.
Ом.

Схема активного двухполюсника с подключённым приёмником энергии Z Н представлена на рис.6.15, где эквивалентная ЭДС двухполюсника
ẺЭ = Ủ2ХХ = 79,47ej12,98 B.
При согласованной нагрузке сопротивление приёмника энергии Z Н равно внутреннему сопротивлению активного двухполюсника Z ВН (см. 5.8.6). То есть
Z Н = Z ВН = 31,79ej60,8 Ом.
Рис 6.15. Схема активного двухполюсника с приёмником энергии
Тогда ток приёмника энергии определяется по формуле.
Ỉ =  A.
A.
Задача №4.
Для электрической цепи рис. 6.16
1. в соответствии с табл. 6.9 нарисовать схему замещения (вариант выбирается по последним цифрам зачетки);
2. по данным табл. 6.10 определить комплексы действующего значения ЭДС всех фаз источника электрической энергии и сопротивления ветвей электрической цепи;
3. по заданным параметрам электрической цепи рассчитать фазные и линейные токи, а также ток в нейтральном проводе;
4. определить напряжение на всех элементах электрической цепи;
5. проверить расчет по балансу мощности;
6. построить потенциальную (топографическую) диаграмму напряжений и векторную диаграмму токов электрической цепи.

Рис. 6.16. Схема электрической цепи
Таблица 6.9. Вид сопротивления ветвей электрической цепи
| Вариант | Z 1 | Z 2 | Z 3 | Z 4 | Нейтраль ный провод |
| R1 + jXL1 | R2 | R3 -j XC2 | R3 | есть | |
| R1 - j XC2 | jXL3 + R3 | R2 | - j XC3 | нет | |
| R3 | R1 - j XC1 | jXL3 + R2 | jXL2 | есть | |
| R1 + j XL1 | - jXC3 + R2 | R3 | R1 | нет | |
| R3 + j XL1 | R2 | R1 - jXC2 | - j XC1 | есть | |
| R2 - j XC2 | jXL3 + XC2 | R1 | R3 | нет | |
| R2 | R1 - j XC2 | jXL3 + R3 | jXL1 | есть | |
| jXL2 + R3 | -jXC1 + R1 | R2 | - j XC3 | нет | |
| R1 + j XL3 | R2 - jXC1 | R3 | R2 | есть | |
| R3 - j XC1 | R1 | R2 + jXL2 | jXL3 | нет | |
| R2 + j XL3 | R1 - jXC3 | R3 | - j XC2 | есть | |
| R1 | R3 - jXC2 | R2 + j XL1 | jXL2 | нет | |
| jXL1 + R3 | R1 | - jXC3 + R2 | R3 | есть | |
| - jXC1 + R1 | R3 | R2 + jXL2 | - j XC3 | нет | |
| R1 | R2 - jХC2 | R3 + j XL3 | R2 | есть | |
| R3 + j XL1 | - jXC1 + R1 | R2 | jXL3 | нет | |
| R2 | jXL2 + R1 | R3 - j XC3 | - j XC1 | есть | |
| R3 - jXC1 | R2 | R1 + jXL2 | jXL1 | нет | |
| R3 + j XL2 | R1 - jXC3 | R2 | R1 | есть | |
| R1 | R2 - jXC3 | R3 + j XL1 | - j XC2 | нет | |
| R3 - j XC1 | R1 | R2 + jXL3 | R3 | есть | |
| R2 + j XL1 | - jXC2 + R1 | R3 | jXL2 | нет | |
| R1 | R2 + j XL2 | - jXC3 + R3 | - j XC3 | есть | |
| R3 - jXC3 | R1 | R2 + j XL2 | jXL3 | нет | |
| R2 - j XC2 | R3 | jXL1 + R1 | R1 | есть | |
| R3 | R2 + jXL1 | R1 - j XC3 | - j XC1 | нет | |
| R3 + jXL2 | R1 | R2 - jXC1 | R2 | есть | |
| R3 - j XC3 | R1 + jXL3 | R2 | jXL1 | нет | |
| R2 | R1 - j XC1 | R3 + jXL2 | - j XC2 | есть | |
| R2 + j XL3 | - jXC1 + R3 | R1 | R3 | нет | |
| R3 + j XL3 | R2 | R1 - jXC2 | jXL2 | есть | |
| R1 | R2 + jXL1 | R3 - j XC2 | - j XC3 | нет | |
| - jXC2 + R2 | R3 | jXL3 + R1 | jXL1 | есть | |
| R1 - jXC1 | R2 + j XL2 | R3 | R1 | нет | |
| R1 | R3 - jXC3 | R2 + j XL1 | - j XC2 | есть | |
| R3 - jXC2 | R1 | R2 + jXL3 | R2 | нет | |
| R2 + j XL3 | R1 - jXC2 | R3 | jXL2 | есть | |
| R3 | R2 - jXC1 | jXL1 + R1 | - j XC2 | нет | |
| R1 -jXC2 | R2 | R3 + j XL2 | jXL1 | есть | |
| R3 | R2 - j XC3 | R1 + jXL3 | R1 | нет | |
| - j XC2 + R2 | R3 + jXL1 | R1 | - j XC1 | есть | |
| jXL3 + R3 | R2 | R1 - j XC1 | R3 | нет | |
| R3 - j XC3 | jXL2 + R1 | R2 | jXL3 | есть | |
| R1 | R3 - j XC2 | R2 + jXL1 | - j XC3 | нет | |
| R3 + j XL1 | -jXC3 + R2 | R1 | R3 | есть | |
| jXL3 + R2 | R3 | R1 - jXC2 | jXL1 | нет | |
| R1 | jXL1 + R3 | -j XC2 + R2 | - j XC1 | есть | |
| R2 - jXC3 | R1 | R2 + jXL1 | jXL3 | нет | |
| -jXC2 + R1 | R2 + j XL3 | R3 | R1 | есть | |
| R3 | R1 - jXC1 | R2 + j XL2 | - j XC2 | нет | |
| R1 - j XC1 | R3 | R2 + jXL3 | R2 | есть | |
| R3 + j XL3 | -jXC2 + R1 | R2 | jXL2 | нет | |
| R2 | R3 - jXC1 | R1 + j XL2 | - j XC3 | есть | |
| R2 | - jXC3 + R3 | R1 + j XL1 | jXL 3 | нет | |
| R3 + j XL3 | R2 | R1 - jXC2 | R1 | есть | |
| - jXC1 + R2 | R1 + j XL2 | R3 | - j XC2 | нет | |
| R3 | R1 - j XC1 | jXL3 + R2 | jXL1 | есть | |
| R2 | jXL2 + R1 | R3 - j XC3 | R3 | нет | |
| jXL1 + R2 | R1 | - jXC2 + R3 | - j XC3 | есть | |
| R1 + j XL1 | R3 - jXC3 | R2 | R1 | нет | |
| R1 - jXC2 | R2 | R3 + jXL3 | jXL2 | есть | |
| R3 | R2 + jXL1 | R1 - j XC2 | - j XC1 | нет | |
| R3 + jXL3 | R1 | - jXC1 + R2 | R2 | есть | |
| R3 - j XC3 | R2 | R1 + jXL2 | jXL1 | нет | |
| R2 | R3 + jXL1 | R1 - j XC2 | - j XC3 | есть | |
| R1 + jXL3 | R2 | -jXC1 + R1 | jXL2 | нет | |
| R3 - j XC3 | R1 + jXL2 | R2 | R3 | есть | |
| jXL1 + R3 | R1 | R2 - jXC2 | - j XC1 | нет | |
| R3 | jXL3 + R2 | - jXC1 + R1 | jXL1 | есть | |
| R3 - jXC2 | R2 | R1 + jXL3 | R1 | нет | |
| R1 + j XL2 | -jXC1 + R3 | R2 | - j XC2 | есть | |
| R1 + jXL1 | R2 | R3 - jXC3 | R3 | нет | |
| - jXC3 + R2 | R1 + jXL2 | R3 | jXL3 | есть | |
| R3 | R1 - jXC2 | R2 + jXL1 | - j XC1 | нет | |
| R1 + j XL1 | - jXC3 + R2 | R3 | R1 | есть | |
| R3 + j XL3 | R2 | R1 - jXC2 | jXL1 | нет | |
| R2 | R1 - j XC2 | R3 + jXL1 | - j XC3 | есть | |
| R3 + j XL1 | - jXC3 + R1 | R2 | jXL2 | нет | |
| R1 | R3 + j XL3 | R2 - jXC2 | R3 | есть | |
| R3 | R2 - jXC1 | R1 +jXL2 | - j XC2 | нет | |
| R2 + j XL1 | R3 | R1 - jXC3 | jXL3 | есть | |
| R1 + j XL3 | - jXC2 + R3 | R2 | R1 | нет | |
| R1 - j XC2 | R2 | R3 + jXL1 | - j XC1 | есть | |
| R2 | R1 + jXL3 | R3 - j XC1 | R3 | нет | |
| R1 + jXL1 | R3 | - jXC2 + R2 | jXL2 | есть | |
| R1 | R2 - jXC3 | R3 + j XL1 | - j XC2 | нет | |
| R2 - jXC2 | R3 | jXL3 + R1 | R2 | есть | |
| - jXC2 + R2 | R3 + jXL1 | R1 | jXL3 | нет | |
| R3 + jXL1 | R2 | R1 - jXC3 | - j XC1 | есть | |
| R2 - jXC2 | R3 | R1 + jXL3 | jXL2 | нет | |
| R1 | R2 + jXL1 | R3 - j XC2 | R2 | есть | |
| R1 + jXL3 | R3 | - jXC1 + R1 | - j XC2 | нет | |
| R2 - j XC3 | R1 + jXL2 | R3 | jXL1 | есть | |
| jXL1 + R2 | R1 | R3 - jXC2 | R3 | нет | |
| R1 | R3 + jXL3 | - jXC1 + R2 | - j XC3 | есть | |
| R2 | R3 - j XC3 | R1 + jXL2 | R1 | нет | |
| R3 + j XL2 | - jXC1 + R2 | R1 | jXL3 | есть | |
| R1 | R2 - jXC3 | R3 +j XL1 | - j XC2 | нет | |
| R1 - jXC2 | R3 | R2 + jXL3 | jXL1 | есть | |
| R2 | R3 + jXL1 | R1 - j XC1 | R3 | нет |
Таблица 6.10. Параметры элементов электрической цепи
| Вари- ант | Фаза | ЭДС | Нач. фаза | R1 | R2 | R3 | ХL1 | ХL2 | ХL3 | ХC1 | ХC2 | ХC3 |
| В | Градусы | Ом | Ом | Ом | Ом | Ом | Ом | Ом | Ом | Ом | ||
| ЕА | ||||||||||||
| ЕВ | – 120 | |||||||||||
| ЕС | ||||||||||||
| ЕА | ||||||||||||
| ЕВ | – 120 | |||||||||||
| ЕС | ||||||||||||
| ЕА | ||||||||||||
| ЕВ | – 120 | |||||||||||
| ЕС | ||||||||||||
| ЕА |
Date: 2016-02-19; view: 622; Нарушение авторских прав