
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Ортогональное проецирование. Еще более частный случай, при котором проецирующие лучи перпендикулярны плоскости проекций принято называть ортогональным проецированием
|
|
Еще более частный случай, при котором проецирующие лучи перпендикулярны плоскости проекций принято называть ортогональным проецированием.
В дальнейшем будем рассматривать лишь ортогональное проецирование, т.к. построение плоских изображений основано на этом методе.
Из принципов построения ортогональных проекций вытекают основные свойства ортогонального проецирования, которые здесь приведем без доказательства.
Свойства ортогонального проецирования
v Проекция точки – точка.
v Проекция прямой – прямая.
v Проецирующий луч проецируется в точку.
v Точка принадлежит прямой линии, в случае если одноименные проекции точки принадлежат одноименным проекциям прямой линии.
v Прямые в пространстве параллельны, в случае если их одноименные проекции параллельны.
v Прямой угол проецируется в прямой, в случае если одна из его сторон параллельна плоскости проекций, а другая не перпендикулярна к ней (Теорема о прямом угле).
v Прямая линия параллельна плоскости, в случае если она параллельна любой прямой, принадлежащей заданной плоскости.
v Проекция плоской фигуры – плоская фигура.
v Решение задач начертательной геометрии и дальнейшие построения основываются именно на этих свойствах.
Итак, сущность метода ортогонального проецирования заключается в том, что предмет проецируется на две взаимно перпендикулярные плоскости лучами, ортогональными (перпендикулярными) к этим плоскостям.

Х12– линия пересечения плоскостей
П1– горизонтальная плоскость проекций.
П2– фронтальная плоскость проекций.
А1– горизонтальная проекция точки.
А2– фронтальная проекция точки.
Чтобы получить плоский чертеж (эпюр Монжа), состоящий из указанных выше проекций, плоскость П1совмещают вращением вокруг оси Х12 с плоскостью П2. Проекционный чертеж, на котором плоскости проекций со всеми изображениями на них, совмещены определенным образом одна с другой, называется эпюром (от франц. еpure- чертеж) (рис. 8). Заменив наглядное изображение эпюром, мы утратили пространственную картину расположения плоскостей проекций и точки. Но эпюр обеспечивает точность и удобноизмеряемость изображений при значительной простоте построений.
При таком способе совмещения плоскостей П1и П2, проекции А1и А2 окажутся расположенными на одном перпендикуляре к оси Х12. Прямые линии, соединяющие разноименные проекции точки на эпюре, называются линиями проекционной связи, которые всегда должны быть перпендикулярны к оси.

Рис. 8 Эпюр точки в системе двух плоскостей проекций
3. Эпюр точки в системе трех плоскостей проекций

В систему плоскостей π1/π2 введём ещё одну плоскость проекций π3, перпендикулярную как к π1, так и к π2. π3 -профильная плоскость проекций. Линии пересечения трёх плоскостей образуют координатные оси, пересекающиеся в точке О, которая является началом координат.
На чертеже показано построение проекций точки А в системе трёх плоскостейт.е. на три плоскости проекций; опустив перпендикуляры на эти плоскости, получаем соответственно горизонтальную (А'), фронтальную (А ") и профильную (А '") проекции точки А.
Перейдём к плоскому изображению, совместив плоскости π1 и π3 с плоскостью π 2 поворотом каждой на 90°, как показано на чертеже стрелками.
Получим эпюр точки А в системе трёх плоскостей проекций. При этом ось Y как бы раздвоилась - одна её часть ушла вниз с плоскостью π1, а вторая - вправо с плоскостью π3.
На эпюре горизонтальная (А') и фронтальная (А") проекции точки А лежат на одной линии связи, которая перпендикулярна оси X; фронтальная (А") и профильная (А"') - на линии связи, перпендикулярной к оси Z; профильная проекция (А"') находится на таком же расстоянии от оси Z, как и горизонтальная (А') от оси X.
4. Способы задания плоскости на эпюре
На эпюре плоскость может быть задана графически одним из следующих способов:
1) тремя точками, не лежащими на одной прямой;
2) прямой и точкой вне её;
3) двумя пересекающимися прямыми;
4) двумя параллельными прямыми;
5)плоской фигурой
Каждый из перечисленных способов задания плоскости легко может быть преобразован в другой.
Кроме того, плоскость на эпюре может быть задана следами. Следом плоскости αназывается линия пересечения этой плоскости с плоскостью проекций. В системе трех плоскостей проекций π1, π2, π3 плоскость общего положения имеет три следа:
hоа- горизонтальный след плоскости α;
foa - фронтальный след плоскости α;
pоа- профильный след плоскости α.
На месте пересечения плоскости α с осями получаем точки, называемые точками схода следов
Иногда плоскость может быть задана координатами точек схода следов.


5. Эпюр прямой. Положение прямой относительно плоскости проекций

Рис: Эпюр прямой
Относительно плоскостей проекций прямая может занимать различное положение. Прямую, не параллельную ни одной из основных плоскостей проекций (см. рис. 69), называют прямой общего положения. Прямую, параллельную или перпендикулярную одной из плоскостей проекций, называют прямой частного положения.
Прямые, параллельные одной из плоскостей проекций, называют прямыми уровня. Название их зависит от того, какой плоскости они параллельны. Прямую, параллельную горизонтальной плоскости проекций, называют горизонталью и обозначают на чертежах h (рис. 70).
Прямую, параллельную фронтальной плоскости проекций, называют фронталью и обозначают f (рис.71).

Рис. 69

Рис. 70

Рис. 71

Рис. 72
Прямую, параллельную профильной плоскости проекций, называют профильной и обозначают р (рис. 72).
У прямой уровня одна проекция параллельна самой прямой и определяет углы наклона этой прямой к двум другим плоскостям проекций.
Параллельность одной из плоскостей проекций определяет расположение двух других проекций прямой уровня:
h2 || П2/П1 ;
h3 _|_ П2/П3 ;
f 2 || П2/П1;
f 3 _|_ П2/П3 ;
p1 _|_ П2/П1 ;
p2 _|_ П2/П1 ;
Прямые h2 и f1 перпендикулярны вертикальным линиям связи; р1 и р2 располагаются на одной вертикальной линии связи и при двух проекционном чертеже должны быть определены двумя точками прямой р.
Прямые, перпендикулярные одной из плоскостей проекций, называются проецирующими. Эти прямые, будучи перпендикулярными одной плоскости проекций, оказываются параллельными двум другим плоскостям проекций. Поэтому у проецирующих прямых одна проекция превращается в точку, а две другие проекции параллельны самой

Рис. 73
прямой и совпадают на чертеже с направлением линии связи (рис. 73). Различают горизонтально проецирующие прямые (АВ), фронтально проецирующие прямые (CD) и профильно проецирующие прямые (EF).
6. Определение натуральной величины отрезка методом прямоугольного треугольника
Сущность данного метода заключается в нахождении гипотенузы прямоугольного треугольника, у которого один катет равен горизонтальной (или фронтальной) проекции отрезка, а величина другого катета представляет собой разность удаления концов отрезка от горизонтальной (или, соответственно, фронтальной) плоскости проекции.
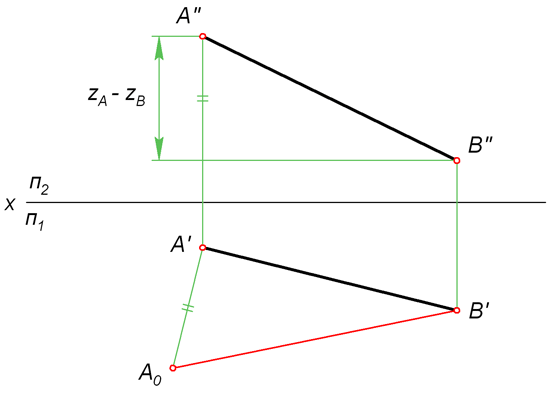
Для того чтобы найти натуральную величину отрезка AB (рисунок выше), строим прямоугольный треугольник A0A'B'. Его первый катет A'B' – это горизонтальная проекция AB. Второй катет A'A0 равен величине ZA – ZB, то есть разности удаления точек A и B от горизонтальной плоскости П1.
Откладываем A'A0 = ZA – ZB перпендикулярно A'B'. Затем проводим гипотенузу A0B' треугольника A0A'B'. На рисунке она обозначена красным цветом. Её величина соответствует настоящей длине AB.
7. Следы прямой.
Следами прямой называют точки её пересечения с плоскостями проекций. В зависимости от того, какую плоскость проекций пересекает прямая в данной точке, различают горизонтальный, фронтальный и профильный след.
Прямые, занимающие общее положение, пересекают три плоскости проекций, линии уровня – две, а проецирующие прямые – одну.
Алгоритм построения следов на эпюре
Найдем следы прямой a, заданной отрезком AB. Как видно на рисунке ниже, AB занимает общее положение, поэтому для решения задачи необходимо построить проекции трех точек.

1. Горизонтальный след Ha. Продлим фронтальную проекцию прямой a до пересечения с осью X в точке Ha''. Полученная точка – фронтальная проекция горизонтального следа. По линии связи на a' найдем точку Ha'. Она является горизонтальной проекцией горизонтального следа и совпадает с т. Ha.
2. Фронтальный след Fa. Продлим горизонтальную проекцию a' до пересечения с осью X в точке Fa'. Полученная точка – горизонтальная проекция фронтального следа*. По линии связи на прямой a'' найдем точку Fa". Она является фронтальной проекцией фронтального следа и совпадает с т. Fa.
3. Профильный след Wa строится аналогично. Для нахождения двух его проекций, Wa'' и Wa', необходимо продлить a'' и a' до пересечения с осью Z.
На следующем рисунке показано построение следов горизонтали b, заданной отрезком CD. Как и другие линии уровня, горизонталь пересекает только две плоскости проекций.

8. Положение плоскости относительно плоскостей проекций
Плоскость относительно плоскостей проекций может занимать следующие положения:
1 - не перпендикулярно к плоскостям проекций;
2 - перпендикулярно к одной плоскости проекций;
3 - перпендикулярно к двум плоскостям проекций.
Плоскость, не перпендикулярную данным плоскостям проекций, называют плоскостью общего положения
Во втором и третьем случаях плоскости называют плоскостями частного положения.
Плоскость, перпендикулярная одной плоскости проекций.
Такие плоскости получили название проецирующих плоскостей. Горизонтально проецирующей плоскостью называют плоскость, перпендикулярную к плоскости проекций П 1 (рис.3.7).
 Рис. 3.7-а
Рис. 3.7-а 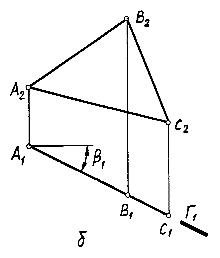 Рис. 3.7-б
Рис. 3.7-б
Любой элемент, лежащий в этой плоскости, проецируется на плоскость П 1 в прямую Г 1, называемую горизонтальным следом плоскости. Угол наклона b горизонтально проецирующей плоскости к плоскости проекций П 2 на комплексном чертеже определяется как угол b 1, заключенный между горизонтальным следом Г 1 данной плоскости и прямой, перпендикулярной линиям связи (рис.3.7-б).
 Рис. 3.8-а
Рис. 3.8-а  Рис. 3.8-б
Рис. 3.8-б
Фронтально проецирующей плоскостью (рис.3.8) называют плоскость, перпендикулярную к плоскости проекций П 2. Любой элемент этой плоскости проецируется на фронтальную плоскость проекций в прямую Ф 2 - фронтальный след плоскости. Угол наклона a фронтально проецирующей плоскости к плоскости П 1 на комплексном чертеже определяется как угол a 2, заключенный между фронтальным следом Ф 2 и прямой, перпендикулярной линиям связи.
Профильно проецирующей плоскостью называют плоскость, перпендикулярную к профильной плоскости проекций (рис.3.9). Любой элемент, лежащий в этой плоскости, проецируется на профильную плоскость проекций в прямую S 3 - профильный след плоскости. На профильной проекции углы a и b наклона профильно проецирующей плоскости к плоскостям П 2 и П 2 изображаются без искажения.
 Рис. 3.9.\
Рис. 3.9.\
9. Главные линии плоскости. Линия наибольшего наклона плоскости
Главные линии плоскости - это особые прямые, принадлежащие плоскости, позволяющие более точно выявить ориентацию плоскости относительно плоскостей проекций и упростить решение многих задач.
Главными линиями плоскости являются прямые уровня: горизонталь h, фронталь f и профильная р, а также линии наибольшего наклона, при помощи которых можно определить угол наклона плоскости к плоскостям проекций П 1, П 2, П 3.
 Рис. 3.13.
Рис. 3.13.
Линиями наибольшего наклона называют прямые данной плоскости перпендикулярные к прямым уровня этой плоскости. Прямая а наибольшего наклона плоскости Г (рис.3.1З-а) к плоскости проекций П 1 образует со своей проекцией а 1 на эту плоскость линейный угол двугранного угла плоскостей Г и П 1. При этом плоскость S (aÇa 1) перпендикулярна прямой h пересечения этих плоскостей и, следовательно, a ^ h и a 1^ h 1. Так как h 1^ h и h 11^ h 1, то a ^ h 1 и a 1^ h 11. Поэтому линия наибольшего наклона данной плоскости к плоскости П 1перпендикулярна к любой горизонтали этой плоскости, и ее горизонтальная проекция перпендикулярна горизонтальной проекции любой горизонтали плоскости. Линию наибольшего наклона к П 1 часто называют линией ската.
Проведя аналогичные рассуждения относительно данной плоскости и П 2, можно заключить, что линия наибольшего наклона плоскости к П 2перпендикулярна к любой фронтали данной плоскости.
На рис.3.13-6 проведены: через точку С - горизонталь; через А - фронталь; через В - линия наибольшего наклона к П 1 (^ h) и линия наибольшего наклона к П 2 (^ f).
10. Условие принадлежности точки плоскости. Привести примеры
Date: 2016-02-19; view: 1527; Нарушение авторских прав