Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Контрольной работы. Задача № 1. К решению этой задачи можно приступить только после изучения тем «основные понятия и аксиомы статики»
|
|
Задача № 1. К решению этой задачи можно приступить только после изучения тем «Основные понятия и аксиомы статики», «Плоская система сходящихся сил».
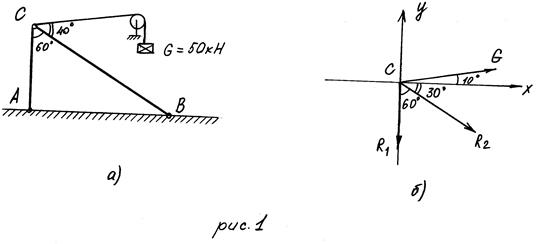
Пример: Определить усилия в стержнях простейшей стержневой конструкции от приложенной в точке С внешней силы (рис. 1, а). Задачу выполнить графическим и аналитическим способами.
|
Аналитический способ решения.
1. Указываем точку, равновесие которой рассматривается. В задачах для контрольной работы такой точкой является точка пересечения всех стержней и нити (в нашем примере – точка С).
2. Составляем расчётную схему конструкции (рис. 1, б). Для этого прикладываем к рассматриваемой точке активную силу. В задачах для контрольной работы активной силой является вес груза. При наличии блока вес груза действует на рассматриваемую точку вдоль нити. Направление силы указываем от точки С, учитывая, что нить всегда испытывает растяжение. Мысленно отбрасываем связи, заменяя их действия реакциями связей. В задачах контрольной работы связями являются идеально жёсткие прямолинейные стержни и нить. При замене связей их реакциями следует помнить, что реакции стержней и нити направлены по их осям. При этом направление реакции стержня заранее неизвестно, поэтому оно может быть принято произвольно. Если направление реакции стержня трудно определить, то его принимают растянутым, а реакцию направляют от рассматриваемой точки. В нашем примере – R1 и R2.
Истинное направление будет установлено после решения уравнений. Реакции нити и стержня принято называть усилиями.
К рассматриваемой точке прикладываем реакции связей. В результате получили систему трёх сил R1; R2; G, сходящихся в одной точке С. Активная сила G известна, а реакции связей R1 и R2 неизвестны (рис. 1, б).
3. Выбираем положение прямоугольной системой координат. Начало координат совмещаем с точкой, равновесие которой рассматривается в нашем примере – точка С. Положение осей может быть выбрано произвольно и на конечном результате при правильном решении это не отражается. Обычно используют один из 2-ух приёмов для выбора направления осей координат. Первый: одну из осей (любую) направляют так, чтобы она совпадала с направлением одной из неизвестных реакций, а другая при этом составляла бы с первой угол 90º. Второй: ось y направляют вертикально, а ось х – горизонтально. Во всех случаях следует определить углы между реакциями и координатными осями и указать их на расчётной схеме.
4. Составляем уравнения равновесия вида:  x = 0;
x = 0;  у = 0, т.к. для равновесия узла С должны равняться нулю алгебраическая сумма проекций всех сил на ось х и ось у. При этом необходимо помнить, что проекцией силы на ось является произведение модуля (величины) силы на косинус угла между направлениями действия силы и оси. Если угол между направлениями силы и оси острый, т.е. сила и ось направлены в одну сторону, то величина проекции положительна, если они направлены в противоположные стороны, т. е. угол между их направлениями тупой, то величина проекции будет отрицательна.
у = 0, т.к. для равновесия узла С должны равняться нулю алгебраическая сумма проекций всех сил на ось х и ось у. При этом необходимо помнить, что проекцией силы на ось является произведение модуля (величины) силы на косинус угла между направлениями действия силы и оси. Если угол между направлениями силы и оси острый, т.е. сила и ось направлены в одну сторону, то величина проекции положительна, если они направлены в противоположные стороны, т. е. угол между их направлениями тупой, то величина проекции будет отрицательна.
Получаем систему двух уравнений с двумя неизвестными. При этом если одна из осей совпадает с неизвестной реакцией, то одно из двух уравнений содержит только одно неизвестное, что упрощает решение системы.
В нашем примере мы получаем следующую систему уравнений:
 x: G∙Cos10˚+ R2•Cos30˚= 0 (1)
x: G∙Cos10˚+ R2•Cos30˚= 0 (1)
 у: - R1 – R2∙Cos60˚ + G∙Cos80˚= 0 (2)
у: - R1 – R2∙Cos60˚ + G∙Cos80˚= 0 (2)
Из первого уравнения находим:
R2 = -  = -
= - 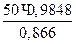 = -56,86 кН ≈ - 57кН.
= -56,86 кН ≈ - 57кН.
Знак минус свидетельствует о том, что стержень СВ не растянут, как предполагалось, а сжат.
Из второго уравнения находим:
R1 = - R2 ∙Cos60 + G∙Cos80 = 56,86∙0,5 + 50∙0,1736 = 37,11 кН ≈ 37 кН.
Усилия в стержнях соответственно равны:
R1 (стержень СА) = 37 кН (растяжение)
R2 (стержень СВ) = 57 кН (сжатие).
Решение задачи обязательно следует проверить. Лучшим способом проверки может быть решение задачи иным способом, например, графическим.
Графический способ решения
Графическое решение задачи выполняется с помощью линейки с миллиметровой шкалой и транспортира.
1. Рассматриваем равновесие той же точки С, в которой сходятся стержни и нить. Усилия в стержнях нам неизвестны, а усилие в нити равно по абсолютному значению величине G из-за отсутствия трения на блоке.
2. Выбираем масштаб сил, например 20 кН в 1 см, и строим силовой многоугольник. Построение начинают с известного усилия. В нашем примере – усилие в нити (G = 50 кН). Из произвольной точки а проводим отрезок аb, параллельный и равный в принятом масштабе силе натяжения G (длина отрезка равна 2,5 см и расположен под углом 10˚ к горизонтальной линии).
|
|

 Главное в решении задач графическим способом
Главное в решении задач графическим способом

 10˚ строго соблюдать параллельность линий.
10˚ строго соблюдать параллельность линий.
Из конца и начала отрезка ab проводим прямые параллельные стержням АС и ВС до их пересечения.
Из точки а ведём линию, параллельную стержню СВ, а из точки b - линию, параллельную СА. Получили силовой треугольник.
|
|


 то силовой треугольник должен быть замкнут. Следователь- но, все стрелки в нём направлены в одну сторону по обходу треугольника, причём это направление определяется направлением известной силы G. Стороны треугольника дают величины и направления реакций R1 и R2 стержней СА и СВ. Измерив в принятом масштабе длины сторон треугольника, получим числовые значения реакций, а следовательно и усилий в стержнях.
то силовой треугольник должен быть замкнут. Следователь- но, все стрелки в нём направлены в одну сторону по обходу треугольника, причём это направление определяется направлением известной силы G. Стороны треугольника дают величины и направления реакций R1 и R2 стержней СА и СВ. Измерив в принятом масштабе длины сторон треугольника, получим числовые значения реакций, а следовательно и усилий в стержнях.
R1 = 1,85 см. Умножив это значение на масштаб, получим R1 = 37кН.
R2 = 2,85. Умножив это значение на масштаб, получим R2 = 57 кНю
Следует отметить, что силовой многоугольник показывает действительное, а не предполагаемое направление искомых сил.
Задача № 2. К решению этой задачи можно приступать после изучения тем «Пара сил» и «Плоская система произвольно расположенных сил». Необходимо твёрдо усвоить условия равновесия плоской системы произвольно расположенных сил и уметь составлять для такой системы уравнения равновесия в трёх формах:
I.  x = 0;
x = 0;  МА = 0;
МА = 0;  МВ = 0.
МВ = 0.
II.  x = 0;
x = 0;  у = 0;
у = 0;  М = 0.
М = 0.
III.  МА = 0;
МА = 0;  МВ = 0;
МВ = 0;  МС = 0.
МС = 0.
для плоской системы параллельных сил – в двух формах:
I.  МА = 0;
МА = 0;  МВ = 0.
МВ = 0.
II.  у = 0;
у = 0;  М = 0.
М = 0.
Особое внимание должно быть уделено изучению основных трёх типов опор балочных систем и умению определять их реакции. Не вдаваясь глубоко в теорию данного вопроса, отметим следующее.
|
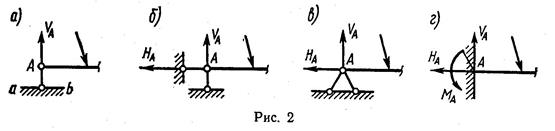
Шарнирно-подвижная опора (рис. 2, а) препятствует лишь поступатель-
ному перемещению тела по нормали к опорной плоскости и, следовательно, накладывает на него одну связь, что символизируется одним стержнем с двумя идеальными (без трения) шарнирами на концах (рис. 2, а), перпендикулярным опорной плоскости (на рисунке к прямой аb). Реакция такой опоры проходит через центр опорного шарнира и направлена вдоль опорного стержня.
Шарнирно- неподвижная опора (рис. 2, б, в) накладывает на тело две связи (она препятствует поступательным перемещениям вдоль обеих координатных осей). Опорная реакция проходит через центр шарнира и содержит две составляющие, неизвестные по значению, что и символизируется двумя опорными стержнями-носителями этих реакций, пересекающимися в точке А.
Защемляющая неподвижная опора (рис. 2, г) не допускает ни линейных, ни угловых перемещений. Развиваемая ею реакция содержит три неизвестных. Эту реакцию можно представить как сечение реактивного момента в опорном сечении с реакцией шарнирно-неподвижной опоры. Балка с защемлённой опорой называется консолью.
|
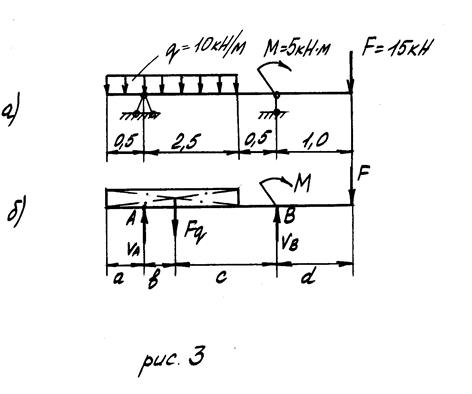
1. Заменяем распределённую нагрузку её равнодействующей, которая является сосредоточенной силой Fq. Для равномерно распределённой нагрузки равнодействующая равна произведению интенсивности нагрузки q на длину участка l, на котором она действует Fq = q• l = 10•3 = 30 кН. Линия действия равнодействующей проходит через середину участка, занятого равномерно распределённой нагрузкой. На расчётной схеме (рис. 3, б) должны быть представлены расстояния от сил до каждой из опор а = 0,5 м; b = 1,0 м; с = 2,0; d = 1,0 м.
2. Обозначаем опоры. Общепринято их обозначать буквами А и В. Простая балка имеет одну шарнирно-неподвижную и вторую шарнирно-подвижную опору.
3. Освобождаемся от опор и заменяем их действие на балку реакциями. В задачах для контрольной работы на балку действуют только вертикальные нагрузки и сосредоточенный момент. Реакции опор при такой нагрузке будут только вертикальными, горизонтальная составляющая шарнирно-неподвижной опоры А будет равна нулю, и её можно не указывать на расчётной схеме. Обычно реакции опор направляют вверх (против действия основной нагрузки) и обозначают реакцию опоры А - VА, а опоры В – VВ.
4. Составляем уравнение равновесия вида: 1)  МА = 0; 2)
МА = 0; 2)  МВ = 0.
МВ = 0.
Следует учесть, что моментом силы относительно точки называется произведение этой силы на плечо – кратчайшее расстояние от рассматриваемой точки до точки приложения силы (в общем случае до линии действия силы).
Если сила стремится повернуть балку относительно рассматриваемой точки по часовой стрелке, то будем считать её момент положительным, а если против – отрицательным. Сосредоточенный момент не умножается на расстояние до опоры, а правило знаков остаётся тем же, что для момента силы.
Первое уравнение для нашей задачи примет вид:
 МА: Fq•b+M-Vв•(b+c) + F(b+c+d) = 0
МА: Fq•b+M-Vв•(b+c) + F(b+c+d) = 0
Fq•1++M-Vв•3+ F•4 = 0
откуда Vв = 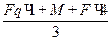 =
= 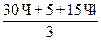 = 31,7 кН.
= 31,7 кН.
Второе уравнение для нашей задачи примет вид:
 МВ = VA•(b+c) - Fq•c+M+F•d = 0
МВ = VA•(b+c) - Fq•c+M+F•d = 0
VA•3 - Fq•2+M+F•1 = 0
откуда VA = 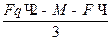 =
= 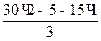 = 13,3 кН.
= 13,3 кН.
5. Выполняем проверку решения. Для этого составляем уравнение равновесия:
 у = 0.
у = 0.  у: VA – Fq + VB – F = 13,3-30+31,7-15 = 0.
у: VA – Fq + VB – F = 13,3-30+31,7-15 = 0.
В нашем случае равенство удовлетворено, следовательно, реакции найдены правильно. Если равенство не удовлетворяется, то в решении допущена ошибка. Также следует помнить, что значение реактивной силы со знаком «минус», свидетельствует о том, что реактивная сила должна быть направлена вниз, а не вверх, как предполагалось.
Пример 2: Определить опорные реакции балки с одним жёстко защемлённым, другим свободным концом (рис. 4, а).
|
1. Заменяем распределённую нагрузку её равнодействующей (см. пример 1, пункт 1) Fq = 2•1 = 2 кН.
2. Обозначаем опору А.
3. Освобождаем балку от опоры и заменяем её действие реакциями: вертикальной VА, горизонтальной НА и реактивным моментом МА (рис. 4, б).
Т.к. на балку действуют только вертикальные нагрузки и сосредоточенные моменты, то горизонтальная составляющая НА будет равна нулю.
Остаётся определить реактивный момент заделки и реактивную силу VA.
4. Составляем и решаем уравнения равновесия. Для определения вертикальной реакции VA составляем уравнение суммы проекций всех сил на ось у:  у = 0.
у = 0.
Для определения реактивного момента заделки составляем уравнение суммы моментов всех сил относительно точки А:  МА = 0.
МА = 0.
 у: VA – F – Fq = 0
у: VA – F – Fq = 0
откуда VA = F + Fq = 8+2 = 10 кН
 МА: - МA + F•а + М + Fq•(a+b) = 0
МА: - МA + F•а + М + Fq•(a+b) = 0
- МA + F•0,5 + М + Fq•1,5 = 0
откуда: МА = F•0,5 + М + Fq•1,5 = 8•0,5+10+2•1,5 = 17 кН•м.
Положительные значения всех найденных реакций говорят о том, что направления их выбраны правильно.
5. Выполняем проверку решения. Для проверки решения удобно составить уравнение моментов относительно произвольно взятой точки, например В:
 МВ = 0
МВ = 0
 МВ: - МА + VA•(a+b+c)+M-F•(b+c) - Fq•C = -17+10•2+10-8•1,5-2•0,5 = 0.
МВ: - МА + VA•(a+b+c)+M-F•(b+c) - Fq•C = -17+10•2+10-8•1,5-2•0,5 = 0.
Реакции вычислены правильно.
Задача № 3.
Перед тем как приступить к решению этой задачи, следует тщательно изучить тему «Центр тяжести», знать положение центров тяжести простейших геометрических фигур и уметь определять координаты центров тяжести сложных сечений, представляющих собой совокупность простейших геометрических фигур, а также сечений, составленных из стандартных профилей проката (в последнем случае необходимо уметь пользоваться таблицами ГОСТов, приведёнными в приложениях).
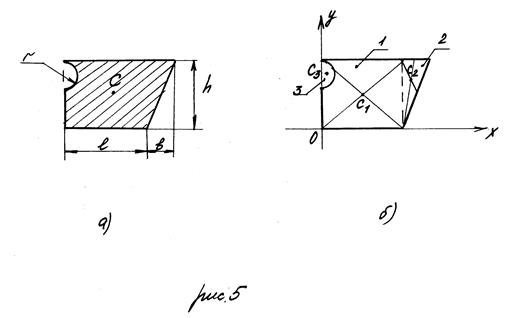
Пример 1. Определить координаты центра тяжести сечения С (рис. 5, а), где h = 60 см; l = 50 см; b = 30 см; r = 10 см.
|
1. Разобьём сечение на элементарные площади: прямоугольник (1), треугольник (2), полукруг (3) (рис. 5, б).
2. Укажем центры тяжести простых фигур С1; С2; С3.
С1 – точка пересечения диагоналей прямоугольника,
С2 – точка пересечения медиан треугольника,
С3 – центральная точка площади полукруга с радиусом r находится на оси симметрии х на расстоянии Xc =  ≈ 0,424 R.
≈ 0,424 R.
3. Выбираем систему координат. Если фигура не имеет оси симметрии, оси координат следует располагать так, чтобы вся фигура находилась в пределах одного квадранта. Ось Х проведём по нижней грани сечения, ось У перпендикулярно ей.
4. Вычислим необходимые данные для определения центра тяжести сечения.
а) площади отдельных геометрических фигур:
S1 = l•h = 50•60 = 3000 см2
S2 =  •b•h =
•b•h =  = 900 см2
= 900 см2
S3 = 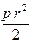 =
= 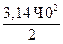 = 157 см2
= 157 см2
б) координаты центров тяжести площадей отдельных геометрических фигур относительно осей (до оси х1; х2; х3 – расстояние от центров С1; С2; С3 до оси
У; у1, у2, у3 - расстояние от центров С1; С2; С3 до оси Х).
х1 = 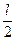 = 25 см у1 =
= 25 см у1 =  = 30 см
= 30 см
х2 = l +  = 50 +
= 50 + 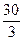 = 60 см у2 =
= 60 см у2 =  =
=  = 40 см
= 40 см
х3 =  =
= 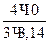 = 4,25 см у3 = h-r = 60-10 = 50 см
= 4,25 см у3 = h-r = 60-10 = 50 см
5. Определим положение центра тяжести заданного сложного сечения по формулам:
xc = 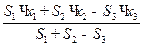 yc=
yc= 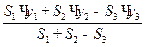
Площадь S3 со знаком «минус», т.к. этой площади в сечении нет, третья фигура – отверстие.
xc =  = 34,29 см
= 34,29 см
yc =  = 31,57 см
= 31,57 см
Ответ: С (34,29; 31,57)
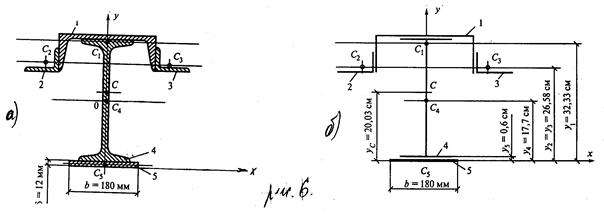
Пример 2. Определить положение центра тяжести сечения, составленного из профилей проката. Сечение состоит из двутавровой балки № 33, швеллера № 27, двух уголков 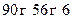 мм и листа сечением 12
мм и листа сечением 12 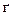 180 мм (рис. 6, а)
180 мм (рис. 6, а)
|
Порядок решения тот же, что в предыдущей задаче. Все необходимые размеры и характеристики профилей приведены в таблицах ГОСТа, называемых сортаментом прокатных профилей (приложения 2-5).
1. разбиваем сечение в соответствии с профилями проката и обозначим их:
1 – швеллер № 27
2, 3 – уголки неравнополочные 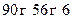 мм
мм
4 – двухтавровая балка № 33
5 – лист сечением 12 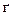 180 мм.
180 мм.
2. Пользуясь приложениями укажем центры тяжести каждого профиля и обозначим их С1; С2; С3; С4; С5. (рис. 6, а).
3. Выбираем систему осей координат. При этом необходимо помнить, что если фигура имеет плоскость симметрии, ось симметрии или центр симметрии, то центр тяжести фигуры находится соответственно в плоскости симметрии, на оси симметрии или в центре симметрии. Ось y совместим с осью симметрии, а ось x направим перпендикулярно оси y и проведём по нижней грани листа (рис. 6, б).
4. Выпишем из приложений необходимые данные для определения центра тяжести сечения.
а) площади отдельных профилей проката:
А1 = 35,2 см2
А2 = А3 = 8,54 см2
А4 = 53,8 см2
А5 = a•b = 1,2•1,8 = 21,6 см2
б) координаты центров тяжести отдельных профилей проката.
Т.к. ось у совпадает с осью симметрии, то она проходит через центр тяжести сечения, поэтому xc = 0. В нашем примере остаётся определить координату yc.
y1 =  листа + hдв. + dшв. – z0(шв.) = 1,2+33+0,6-2,47 = 32,33 см
листа + hдв. + dшв. – z0(шв.) = 1,2+33+0,6-2,47 = 32,33 см
y2 =  листа hдв. + dшв. – bшв. + x0(уч.) = 1,2+33+0,6-9,5+1,28 = 26,58 см
листа hдв. + dшв. – bшв. + x0(уч.) = 1,2+33+0,6-9,5+1,28 = 26,58 см
y3 = y2 = 26,58 см
y4 =  листа +
листа +  = 1,2 +
= 1,2 +  = 17,7 см
= 17,7 см
y5 =  =
= 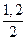 = 0,6 см
= 0,6 см
6. Определим положение центра тяжести заданного сечения
xc = 0
yc = 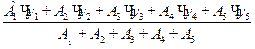 = =
= =  = 20,03 см
= 20,03 см
Ответ: С (0; 20,03).
Задача № 4. К решению этой задачи можно приступать после изучения тем «Основные понятия сопротивления материалов» и «Растяжение и сжатие». Следует помнить, что при работе бруса на растяжение (сжатие) в его поперечных сечениях возникает один внутренний силовой фактор – продольная сила N. Продольная сила в произвольном поперечном сечении бруса численно равна алгебраической сумме проекций на его продольную ось всех внешних сил, приложенных по одну сторону от сечения. При растяжении продольную силу будем считать положительной, при сжатии - отрицательной. Для определения продольной силы применяется метод сечений. Суть этого метода заключается в том, что тело мысленно разрезается плоскостью на две части, любая из которых отбрасывается и взамен неё к сечению оставшейся части прикладываются внутренние силы, заменяющие действие отброшенной части. Оставленная часть рассматривается как самостоятельное тело, находящееся в равновесии под действием внешних сил и внутренних, уравновешивающих внешние. Величину, характеризующую интенсивность внутренних сил, называют напряжением. При растяжении (сжатии) возникают нормальные напряжения  . Числовое значение напряжений в поперечных сечениях тела зависит не только от возникновения силового фактора, но и от размеров поперечного сечения А. Соответственно
. Числовое значение напряжений в поперечных сечениях тела зависит не только от возникновения силового фактора, но и от размеров поперечного сечения А. Соответственно  =
= 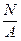 .
.
Согласно формуле единицей напряжения служит паскаль, т. е. 1 Па =  или 1МПа =
или 1МПа = 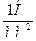 . Изменение продольной силы и напряжения по длине бруса удобно представлять в виде графика, называемого эпюрой. Под действием внешних сил брус удлиняется или укорачивается. Удлинение (укорочение) бруса или отдельных его участков определяется по формуле Гука:
. Изменение продольной силы и напряжения по длине бруса удобно представлять в виде графика, называемого эпюрой. Под действием внешних сил брус удлиняется или укорачивается. Удлинение (укорочение) бруса или отдельных его участков определяется по формуле Гука:
∆l = 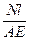 , т.к.
, т.к. 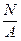 =
=  , то эту формулу можно представить в виде ∆l =
, то эту формулу можно представить в виде ∆l =  •
• 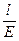 .
.
Если значение ∆l положительно, то брус удлинился, если ∆l – отрицательно, то брус укоротился.
Пример: Для трёхступенчатого бруса (рис.7, а) определить и построить эпюры продольных сил и нормальных напряжений. Определить удлинение (укорочение) бруса. Модуль упругости E = 2•105 МПа.
F1 = 120 кН; F2 = 70 кН; F3 = 150 кН
А1 = 12 см2; А2 = 20 см2; А3 = 18 см2
l1 = 60 см; l2 = 40 см; l3 = 20 см; l4 = 50 см l5 = 10 см.
Проверить прочность бруса, если [  ]p = 120 МПа
]p = 120 МПа
[  ]сж = 100 МПа
]сж = 100 МПа
1. Разбиваем брус на отдельные участки. Нумерацию участков начинают от свободного сечения. Границами участков являются сечения, в которых приложены внешние силы или в которых изменяются размеры поперечного сечения бруса. Первый участок 1 от точки приложения силы F1, т.е. от правого торца до сечения, в котором происходит изменение его размеров. Второй участок 2 до точки приложения силы F2. Третий участок 3 от точки приложения силы F2 до сечения, в котором происходит изменение поперечного размера. Четвёртый участок 4 до точки приложения силы F3 и пятый 5 до заделки.
|
¨ Мысленно рассечём брус по границе первого участка 1 и отбросим левую часть и рассматриваем оставшуюся правую часть в состоянии равновесия. На первом участке действует одна внешняя сила F1, которая уравновешивается внутренней силой N1


|
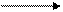 |

Составим уравнение равновесия:
-N1 – F1 = 0
N1 = - F1 = -120 кН.
Продольная сила отрицательна, следовательно, на участке 1 имеет место деформация сжатия.
¨ Проводим сечение по границе второго участка 2 и отбрасываем левую отсечённую часть, рассматривая правую в состоянии равновесия. На втором участке действует также сила F1, которую уравновешивает внутренняя сила N2.
Составляем уравнение равновесия:
-N2 – F1 = 0
N2 = - F1 = -120 кН.

Второй участок сжимается.
¨ Проводим сечение по границе третьего участка 3 и отбрасываем правую часть. По аналогии с предыдущим участком составляем уравнение равновесия. Внутренняя сила N3 уравновешивает две внешние силы F1 и F2.
-N3 + F2 – F1 = 0
N3 = F2 – F1 = 70-120 = -50 кН
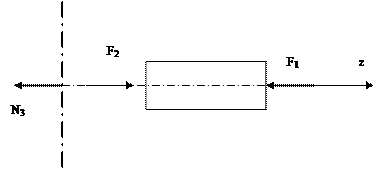
На третьем участке брус также сжат.
¨ Проводим сечение по границе четвёртого участка 4. Рассуждая аналогично составим уравнение равновесия. На четвёртом участке действуют 2 внешние силы F1 и F2, которые уравновешиваются внутренней силой N4.
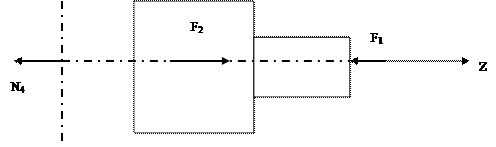 |
-N4 + F2 – F1 = 0
N4 = F2 – F1 = -50 кН.
Четвёртый участок испытывает сжатие.
¨ Проводим последнее сечение по границе пятого участка. Сечение проводится мысленно, немного не доходя до жёсткой заделки (иначе, нужно будет учитывать реактивные силы, возникающие в заделке).
По аналогии составляем уравнение равновесия. Внутренняя сила N5 будет уравновешивать все внешние силы F1; F2; F3.
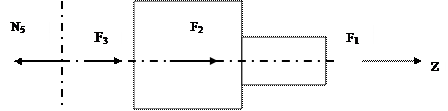 |

-N5 + F3 + F2 – F1 = 0
N5 = F3 + F2 – F1 = 150+70-120 = 100 кН
Пятый участок растянут.
3. Строим эпюру продольных сил N (рис. 7, б). Проведя параллельно оси бруса базовую (нулевую) линию эпюры, откладываем перпендикулярно ей в произвольном масштабе полученные значения N. Выше нулевой линии откладываем значения продольной силы, вызванной растяжением (т.е. положительные значения), а ниже нулевой линии – сжатием (т.е. отрицательные значения). Эпюра оказалась очерченной прямыми линиями, параллельными базовой. При переходе через сечения, проведённые в точках приложения внешних сил, эпюра делает «скачок», равный абсолютному значению приложенной в этом сечении силы.
4. Находим напряжения на отдельных участках бруса по формуле  =
= 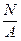 , соблюдая размерность единиц: N – в Ньютонах, А – в квадратных мм.
, соблюдая размерность единиц: N – в Ньютонах, А – в квадратных мм.
 1 =
1 =  = -
= -  = - 100 МПа
= - 100 МПа
 2 =
2 =  = -
= - 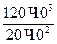 = - 60 МПа
= - 60 МПа
 3 =
3 = 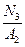 = -
= - 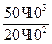 = - 25 МПа
= - 25 МПа
 4 =
4 = 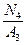 = -
= -  = - 27,8 МПа
= - 27,8 МПа
 5 =
5 = 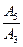 =
= 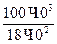 = 55,6 МПа
= 55,6 МПа
5. В соответствии с полученными значениями напряжений строим эпюру нормальных напряжений (рис. 7,6). Правило построения эпюры  то же, что и для эпюры N.
то же, что и для эпюры N.
6. Проверяем прочность ступенчатого бруса. Прочность бруса обеспечена, если выполняется условие:  max ≤
max ≤  , где
, где  max – наибольшее значение напряжения (выбирают из эпюры
max – наибольшее значение напряжения (выбирают из эпюры  );
);  - наибольшее напряжение, которое выдерживает материал бруса. Из эпюры нормальных напряжений выбираем максимальное нормальное напряжение растянутых участков и сравниваем с допустимым:
- наибольшее напряжение, которое выдерживает материал бруса. Из эпюры нормальных напряжений выбираем максимальное нормальное напряжение растянутых участков и сравниваем с допустимым:
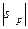 max = 55,6 МПа
max = 55,6 МПа  р = 120 МПа
р = 120 МПа
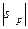 max ≤
max ≤  р
р
55,6 ≤ 120. Условие прочности выполняется. Из эпюры нормальных напряжений выбираем максимальное нормальное напряжение на сжатых участках и сравниваем с допустимым:
 max = 100 МПа
max = 100 МПа  сж = 100 МПа
сж = 100 МПа
 max ≤
max ≤  сж
сж
100 ≤ 100. Условие прочности выполняется.
Вывод: прочность ступенчатого бруса обеспечена.
7. Изменение длины бруса равно алгебраической сумме изменений длин его участников:
∆l = ∆l1 + ∆l2 + ∆l3 + ∆l4 + ∆l5 =  +
+ 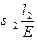 +
+ 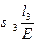 +
+  +
+  =
=
= 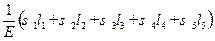 = =
= =  =
= 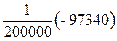 =-0,49 мм.
=-0,49 мм.
Брус укоротился на 0,49 мм.
Задача № 5. Для решения этой задачи необходимо изучить тему «Изгиб прямого бруса» и научиться безошибочно строить эпюры поперечных сил Qх и изгибающих моментов Мх . Алгоритм построения эпюр поперечных сил и изгибающих моментов для простой балки.
1. Определяют опорные реакции балки (см. порядок решения задачи № 2).
2. Обозначают характерные сечения (точки) балки. Ими являются концевые сечения балки, опоры, точки приложения сосредоточенных сил и моментов.
3. Строят эпюру поперечных сил Q. Для этого определяют значения поперечных сил в характерных точках. Следует помнить, что поперечная сила в сечении равна сумме проекций всех сил, расположенных только слева или только справа от рассматриваемого сечения, на ось, перпендикулярную оси элемента. Силу, расположенную слева от рассматриваемого сечения и направленную вверх, считают положительной (со знаком «плюс»), а направленную вниз – отрицательной (со знаком «минус»).
Для правой части балки – наоборот.
В сечениях, соответствующих точкам приложения сосредоточенных сил, в том числе в точках приложения опорных реакций, необходимо определить два значения поперечной силы: чуть левее рассматриваемой точки и чуть правее её. Поперечные силы в этих сечениях обозначаются соответственно Qлев. и Qпр..
Найденные значения поперечных сил в характерных точках откладываются в некотором масштабе от нулевой линии. Эти значения соединяются прямыми линиями. Соединив все значения поперечных сил получим график изменения поперечных сил по длине балки. Такой график называется эпюрой Qх.
4. Строят эпюру изгибающих моментов Mх. Для этого определяют изгибающие моменты в характерных сечениях. Следует помнить, что изгибающий момент в рассматриваемом сечении равен сумме моментов всех сил (сосредоточенных, в том числе опорных реакций и внешних сосредоточенных моментов), расположенных только слева или только справа от этого сечения. Если любое из перечисленных силовых воздействий стремится повернуть левую часть балки по часовой стрелке, то оно считается положительным (со знаком «плюс»), если против – отрицательным (со знаком «минус»), а для правой части наоборот.
В сечениях, соответствующих точкам приложения сосредоточенных моментов, необходимо определить два значения изгибающего момента: чуть левее рассматриваемой точки и чуть правее её. Изгибающие моменты в этих точках обозначаются соответственно Млев. и Мпр..
В точках приложения сил определяется одно значение изгибающего момента. Полученные значения откладываются в некотором масштабе от нулевой линии. Эти значения соединяются прямой линией. Соединив все значения изгибающих моментов по длине балки. Такой график называется эпюрой Мх.
После приобретения достаточных навыков в построении эпюр внутренних усилий следует перейти к тщательному разбору вывода формулы для определения нормальных напряжений при изгибе. Очень важно понять закон распределения этих напряжений по высоте поперечного сечения балки, уметь определять максимальные напряжения, уяснить смысл ещё одной геометрической характеристики сечения – осевого момента сопротивления для симметричных сечений.
Далее следует перейти к изучению расчёта балок на прочность, для чего необходимо запомнить и уметь применять при расчётах условие прочности.
Прочность балки обеспечена, если наибольшие по абсолютному значению нормальные напряжения, возникающие в опасном сечении, не превышают допустимых
 max =
max = 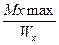 ≤
≤  .
.
Для подбора сечения балки (проектного расчёта) из условия прочности определяют необходимую величину осевого момента сопротивления:
Wx ≥ 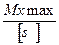 .
.
По найденному моменту сопротивления Wx, выбрав форму поперечного сечения, находят его размеры. Для прямоугольного сечения (рис. 8)
 |
h Wx = 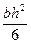
Для круглого сечения: Wx = 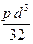
Рис. 8
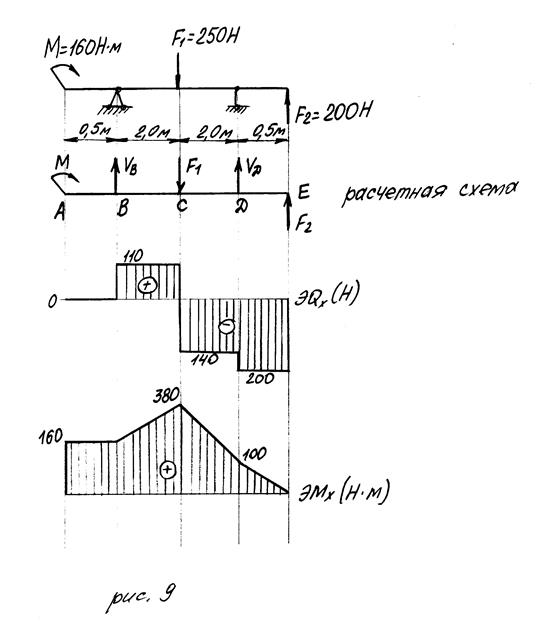
Пример: Для заданной двухопорной балки (рис. 9, а) определить реакции опор, построить эпюры поперечных сил, изгибающих моментов и подобрать необходимые размеры сечения деревянной балки в трёх вариантах:
i. балка имеет круглое сечение
ii. балка имеет прямоугольное сечение, в котором 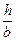 = 1,5.
= 1,5.
Для древесины  = 10 МПа.
= 10 МПа.
|
1. Определим опорные реакции балки. Для этого составим расчётную схему (рис. 9, б), в которой указаны все силы активные и реактивные.
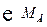 = 0
= 0 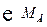 : М + F1•2 - VД•4 – F2•4,5 = 0.
: М + F1•2 - VД•4 – F2•4,5 = 0.
Из первого уравнения найдём VД:
VД =  =
= 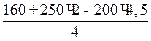 = -60 Н.
= -60 Н.
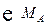 = 0
= 0 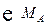 : М+VВ•4 - F1•2 – F2•0,5 =0.
: М+VВ•4 - F1•2 – F2•0,5 =0.
Из второго уравнения найдём VВ:
VВ = 
 =
= 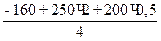 = 110 Н.
= 110 Н.
Выполним проверку:
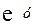 = 0
= 0 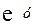 : VВ – F1 + VД + F2 = 110-250-60+200 = 0.
: VВ – F1 + VД + F2 = 110-250-60+200 = 0.
2. Обозначим характерные сечения балки: А, Б, С, Д, Е.
3. Строим эпюру Q. Определим для этого значения поперечных сил в характерных сечениях, ходом слева.
QA = 0
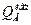 = 0
= 0
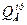 = VВ = 110 Н
= VВ = 110 Н
 = VВ = 110 Н
= VВ = 110 Н
 = VВ – F1 = 110 – 250 = -140 Н
= VВ – F1 = 110 – 250 = -140 Н
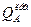 = VВ – F1 = -140 Н
= VВ – F1 = -140 Н
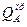 = VВ – F1 + VД = 110-250-60 = -200 Н
= VВ – F1 + VД = 110-250-60 = -200 Н
 = VВ – F1 + VД = -200 Н
= VВ – F1 + VД = -200 Н
 = VВ– F1+ VД + F2 = 110-25-60+200 = 0.
= VВ– F1+ VД + F2 = 110-25-60+200 = 0.
Соединив полученные значения прямыми линиями получим эпюру Qх
(рис. 9, в). В сечениях с сосредоточенно приложенной силой на эпюре Qх возникает скачок (два значения – слева и справа от сечения), по абсолютному значению равный сосредоточенной силе.
4. Строим эпюру Мх. Определим изгибающие моменты в характерных точках, ходом слева.
 = 0
= 0
 = М = 160 Н•м
= М = 160 Н•м
МВ = М = 160 Н•м
МС = М + VВ•2 = 160+110•2 = 380 Н•м
МД = М + VВ•4 – F1•2 = 160+110•4-250•2 = 100 Н•м
МЕ = М + VВ•4,5 - F1•2,5 + VД•0,5 = 160+110•4,5-250•2,5-60•0,5 = 0.
Соединив полученные значения прямыми линиями получим эпюру Мх
(рис. 9, г). Два значения изгибающих моментов появляются в сечениях, где приложен сосредоточенный момент (пара сил). На эпюре соответственно возникает скачок, равный сосредоточенному моменту.
5. Определяем размеры поперечного сечения балки, для чего используем условие прочности при изгибе 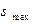 =
= 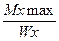 ≤
≤  , из которого следует, что Wx max = 380 Н•м.
, из которого следует, что Wx max = 380 Н•м.  - допускаемое напряжение для материала. В нашем примере материалом бруса является древесина, для которой
- допускаемое напряжение для материала. В нашем примере материалом бруса является древесина, для которой
 = 10 МПа.
= 10 МПа.
Wx =  = 38000 мм3 = 38 см3
= 38000 мм3 = 38 см3
а) сечение круглое
Wx = 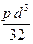 d =
d = 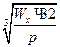 =
= 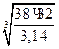 = 7,29 см.
= 7,29 см.
Площадь поперечного сечения Акр =  = 41,72 см2
= 41,72 см2
б) сечение прямоугольное, в котором 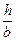 = 1,5
= 1,5
Wx = 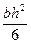 , т.к.
, т.к. 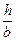 = 1,5, то b =
= 1,5, то b = 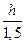 .
.
Следовательно, Wx = 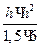 =
= 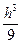
38 = 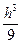 , находим h =
, находим h = 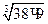 = 7 см
= 7 см
b = 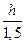 =
=  = 4,7 см.
= 4,7 см.
Площадь прямоугольного сечения Апр = b•h = 7•4,7 = 32,9 см2.
Отношение масс балок одинаковой длины равно отношению площадей сечений: 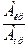 =
= 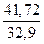 = 1,23.
= 1,23.
Следовательно, балка круглого сечения тяжелее балки прямоугольного сечения в 1,23 раза.
Для справки. Самым рациональным сечением для балок, работающих на изгиб является двутавровое сечение.
Сталь прокатная угловая неравнополочная (ГОСТ 8510—86)
Обозначения:
В — ширина большой полки;
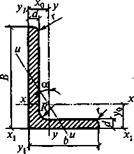 b — ширина малой полки;
b — ширина малой полки;
d — толщина полки;
R — радиус внутреннего закругления;
r — радиус закругления полки;
J— момент инерции;
i — радиус инерции;
x0, У о — расстояния от центра тяжести до наружных граней полок.
| Номер про-, филя | Размеры, мм | Пло- шадь сечения, см2 | Масса 1 м ДЛИНЫ, кг | Справочные величины для осей | Тангенс угла а | |||||||||||||
| В | Ъ | d | R | г | Х-Х | У—У | Х1-Х1 | У1—У1 | и—и | |||||||||
| Jx, см4 | ix, см | Jy,, см4 | iy, см | Jx1, см4 | Уо, см | Jy1, см4 | хо, см | Ju min, см4 | iu min, см4 | |||||||||
| 5,5/3,6 | 4 5 | 3,58 4,41 | 2,81 3,46 | 11,4 13,8 | 1,78 1,77 | 3,7 4,48 | 1,02 1,01 | 23,2 29,2 | 1,82 1,86 | 6,25 7,91 | 0,84 0,88 | 2,19 2,66 | 0,78 0,78 | 0,506 0,404 | ||||
| 6,3/4 | 4 5 6 8 | 2,3 | 4,04 5,98 5,90 7,68 | 3,17 3,91 4,63 6,03 | 16,3 19,9 23,3 29,6 | 2,01 2,00 1,99 1,96 | 5,16 6,26 7,28 9,15 | 1,13 1,12 1,11 1,09 | 33,0 41,4 49,9 66,9 | 2,03 2,08 2,12 2,20 | 8,51 10,80 13,10 17,90 | 0,91 0,95 0,99 1,07 | 3,07 3,73 4,36 5,58 | 0,87 0,86 0,86 0,85 | 0,397 0,396 0,393 0,386 | |||
| 7,4/5 | 7,5 | 2,5 | 5,59 | 4,39 | 27,8 | 2,23 | 9,05 | 1,27 | 56,7 | 2,28 | 15,20 | 1,05 | 5,34 | 0,98 | 0,406 | |||
| 7,5/5 | 5 6 8 | 2,7 | 6,11 7,25 9,47 | 4,79 5,69 7,43 | 34,8 40,9 52,4 | 2,39 2,38 2,35 | 12,5 14,6 18,5 | 1,43 1,42 1,40 | 69,7 83,9 112,0 | 2,39 2,44 2,52 | 20,8 25,2 34,2 | 1,17 1,21 1,29 | 7,24 8,48 10,90 | 1,09 1,08 1,07 | 0,436 0,435 0,430 | |||
| 8/5 | 5 6 | 2,7 | 6,36 7,55 | 4,99 5,92 | 41,6 49,0 | 2,56 2,55 | 12,7 14,8 | 1,41 1,40'' | 84,6 102,0 | 2,60 2,65 | 20,8 25,2 | 1,13 1,17 | 7,58 8,88 | 1,09 1,08 | 0,387 0,386 | |||
| 9/5,6 | 5,5 6 8 | 7,86 8,54 11,18 | 6,17 6,70 8,77 | 65,3 70,6 90,9 | 2,88 2,88 2,85 | 19,7 21,2 27,1 | 1,58 1,58 1,56 | 132,0 145,0 194,0 | 2,92 2,95 3,04 | 32,2 35,2 47,8 | 1,26 1,28 1,36 | 11,80 12,70 16,30 | 1,22 1,22 1,21 | 0,384 0,384 0,380 | ||||
| 10/6,3 | 6 7 8 10 | 3,3 | 9,59 11,10 12,60 15,50 | 7,53 8,70 9,87 12,10 | 98,3 113,0 127,0 154,0 | 3,20 3,19 3,18 3,15 | 30,6 35,0 39,2 47,1 | 1,79 1,78 1,77 1,75 | 198,0 232,0 266,0 333,0 | 3,23 3,28 3,32 3,40 | 49,9 58,7 67,6 85,8 | 1,42 1,46 1,50 1,58 | 18,20 20,80 23,40 28,30 | 1,38 1,37 1,36 1,35 | 0,393 0,392 0,391 0,387 | |||
| 11/7 | НО | 6,5 8 | 3,3 | 11,40 13,90 | 8,98 10,90 | 142,0 172,0 | 3,53 3,51 | 45,6 54,6 | 2,00 1,98 | 286,0 353,0 | 3,55 3,61 | 74,3 92,3 | 1,58 1,64 | 26,90 32,30 | 1,53 1,52 | 0,402 0,400 | ||
| 12,5/8 | 8 10 12 | 3,7 | 14,10 16,00 19,70 23,40 | 11,00 12,50 15,50 18,30 | 227,0 256,0 312,0 365,0 | 4,01 4,00 3,98 3,95 | 73,7 83,0 100,0 117,0 | 2,29 2,28 2,26 2,24 | 452,0 518,0 649,0 781,0 | 4,01 4,05 4,14 4,22 | 119,0 137,0 173,0 210,0 | 1,80 1,84 1,92 2,00 | 43,30 48,80 59,30 69,50 | 1,76 1,75 1,74 1,72 | 0,407 0,406 0,404 0,400 | |||
| 14/9 | 8 10 | 18,00 22,20 | 14,10 17,50 | 364,0 444,0 | 4,49 4,47 | 120,0 146,0 | 2,58 2,56 | 727,0 911,0 | 4,49 4,58 | 194,0 245,0 | 2,03 2,12 | 70,30 85,50 | 1,98 1,96 | 0,411 0,409 | ||||
| 16/10 | 9 10 12 14 | 4,3 | 22,90 25,30 30,00 34,70 | 18,00 19,80 23,60 27,30 | 606,0 667,0 784,0 897,0 | 5,15,5,13 5,11 5,08 | 186,0 204,0 239,0 272,0 | 2,85 2,84 2,82 2,80 | 1221 1359 1634 1910 | 5,19 5,23 5,32 5,40 | 300,0 335,0 405,0 477,0 | 2,23 2,28 2,36 2,43 | 110,0 121,0 142,0 162,0 | 2,20 2,19 2,18 2,16 | 0,391 0,390 0,388 0,385 | |||
| 18/11 | ПО | 10 12 | 4,7 | 28,30 33,70 | 22,20 26,40 | 952,0 1123,0 | 5,80 5,77 | 276,0 324,0 | 3,12 3,10 | 1933 2324 | 5,88 5,97 | 444,0 537,0 | 2,44 2,52 | 165,0 194,0 | 2,42 2,40 | 0,375 0,374 | ||
| 20/12,5 | 11 12 14 16 | 4,7 | 34,90 37,90 43,90 49,80 | 27,40 29,70 34,40 39,10 | 1449,0 1568,0 1801,0 2026,0 | 6,45 6,43 6,41 6,38 | 446,0 482,0 551,0 617,0 | 3,58 3,57 3,54 3,52 | 2920 3189 3726 4264 | 6,50 6,54 6,62 6,71 | 718,0 786,0 922,0 1061 | 2,79 2,83 2,91 2,99 | 264,0 285,0 327,0 367,0 | 2,75 2,74 2,73 2,72 | 0,392 0,392 0,390 0,388 | |||
| 25/16 | 12 16 18 20 | 48,30 63,60 71,10 78,50 | 37,90 49,90 55,80 61,70 | 3147,0 4091,0 4545,0 4987,0 | 8,07 8,02 7,99 7,97 | 1032 1333 145,0 1613 | 4,62 4,58 4,56 4,53 | 6212 8308 9358 10410 | 7,97 8,14 8,23 8,31 | 1634 2200 2487 2776 | 3,53 3,69 3,77 3,85 | 604,0 781,0 866,0 949,0 | 3,54 3,50 3,49 3,48 | 0,410 0,408 0,407 0,405 |
Сталь прокатная – балки двутавровые (ГОСТ 8239—72)
|
Обозначения:
h— высота балки;
b— ширина полки;
d— толщина стенки;
t — средняя толщина полки;
R— радиус внутреннего закругления;
r— радиус закругления полки;
J— момент инерции;
W— момент сопротивления;
S— статический момент полусечения;
i— радиус инерции.
| Номер профиля | Масса 1 м длины, кг | Размеры, мм | Площадь сечения, см2 | Справочные величины для осей | |||||||||||
| h | b | d | t | R | r | х - х | у —у | ||||||||
| Jx, CM2 | Wx, см3 | к, см | Sx, см3 | Jy, СМ4 | Wy, cm3 | iy, см | |||||||||
| 10 12 14 16 18 18а | 9,46 11,5 13,7 15,9 18,4 19,9 | 100 120 140 160 180 180 | 55 64 73 81 90 100 | 4,5 4,8 4,9 5,0 5,1 5,1 | 7,2 7,3 7,5 7,8 8,1 8,3 | 7,0 7,5 8,0 8,5 9,0 9,0 | 2,5 3,0 3,0 3,5 3,5 3,5 | 12,0 14,7 17,4 20,2 23,4 25,4 | 39,7 58,4 81,7 109,0 143,0 159,0 | 4,06 4,88 5,73 6,57 7,42 7,51 | 23,0 33,7 46,8 62,3 81,4 89,8 | 17,9 27,9 41,9 58,6 82,6 114,0 | 6,49 8,72 11,5 14,5 18,4 J22,8 | 1,22 1,38 1,55 1,70 1,88 2,12 | |
| 20 20а 22 22а 24 24а 27 27а 30 30а 33 36 40 45 50 55 60 | 21,0 22,7 24,0 25,8 27,3 29,4 31,5 33,9 36,5 39,2 42,2 48,6 57,0 66,5 78,5 92,6 108,0 | 200 200 220 220 240 240 270 270 300 300 330 360 400 450 500 550 600 | 100 ПО ПО 120 115 125 125 135 135 145 140 145 155 160 170 180 190 | 5,2 5,2 5,4 5,4 5,6 5,6 6,0 6,0 6,5 6,5 7,0 7,5 8,3 9,0 10,0 11,0 12,0 | 8,4 8,6 8,7 8,9 9,5 9,8 9,8 10,2 10,2 10,7 11,2 12,3 13,0 14,2 15,2 16,5 17,8 | 9,5 9,5 10,0 10,0 10,5 20,5 11,0 11,0 12,0 12,0 13,0 14,0 15,0 16,0 17,0 18,0 20,0 |