Методы оценки

Методы оценки распределений и некоторых их моментов при достаточно большом объеме выборки, т.е. числе реализаций N, заключаются, прежде всего, в вычислении математического ожидания M [ ξ ]= μ_ξ и дисперсии D [ ξ ]= σ_ξ², т.е. соответственно первого и второго центральных моментов случайной величины ξ:

где w(x) – плотность распределения случайной величины ξ, принимающей значения x.

При проведении имитационного эксперимента со стохастической моделью системы определить эти моменты невозможно, как правило, из-за неизвестной априори (заранее) плотности распределения w(x). Поэтому при обработке результатов моделирования приходится довольствоваться лишь некоторыми оценками моментов, полученными на конечном числе реализаций N. При условии независимости наблюдений значений случайной величины ξ в качестве таких оценок используются:

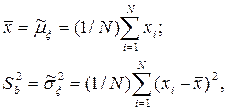
где – выборочное среднее, а – выборочная дисперсия, которые используются в качестве оценок математического ожидания μ_ξ и дисперсии σ_ξ² соответственно.

Оценки, полученные в итоге статистической обработки результатов моделирования, должны удовлетворять следующим требованиям.

1. Несмещенность оценки означает равенство математического ожидания оценки определяемому параметру:

где – оценка параметра g.

2. Эффективность оценки означает минимальность среднего квадрата ошибки данной оценки:

где – рассматриваемая оценка; – любая другая оценка.

3. Состоятельность оценки означает сходимость по вероятности при N→∞ к оцениваемому параметру:

С учетом неравенства Чебышева достаточное условие выполнения этого неравенства заключается в том, чтобы

Date: 2016-02-19; view: 422; Нарушение авторских прав