Приклад 8.4. Первинні параметри лінії на частоті мають такі значення: , , , . Обчислити на даній частоті коефіцієнти ослаблення та фази

Для розрахунків коефіцієнтів 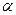та є три формули (8.23) - (8.25). Знайдемо, яка ж саме з них підходить у даному випадку. Для цього обчислимо спочатку 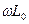та : 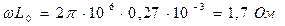; 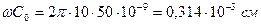. Оскільки виконуються нерівності 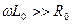та 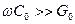, можна використовувати наближені формули (8.24) та (8.25):

;

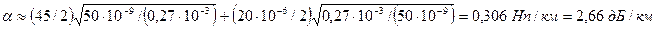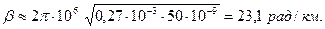
7.4. РЕЖИМ БІЖУЧИХ (ПАДАЮЧИХ) ХВИЛЬ У ЛІНІЇ

Напруга і струм в узгоджено навантаженій лінії. Розглянемо розподіл напруги та струму вздовж узгоджено навантаженої лінії. Для цього скористу­ємося рівняннями (8.21) і підставимо до них ; ; 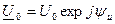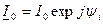. В результаті такої підстановки дістанемо такі формули:

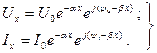(8.26)

Як бачимо, розподіл комплексних напруги та струму вздовж лінії з точ­ністю до позначень визначається однаковими формулами. Тому надалі будемо аналізувати перше рівняння. Отримані результати будуть повністю справедливими і для розподілу струму вздовж лінії.

Рівняння біжучої хвилі. Переходимо тепер до миттєвих значень напруги. З формули (8.26) випливає, що амплітуда напруги 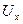дорівнює , а початкова фаза 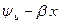. Таким чином, якщо на вході лінії діє напруга 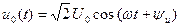,то в будь-якому перерізі на віддалі 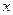від її почат­ку виникає напруга

(8.27)

Як і було очікувано, напруга залежить від двох змінних - часу 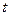та координати .

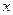Одним із засобів графічного зображення функцій двох змінних є побудова сім'ї графіків для фіксованої однієї змінної та неперервна зміна іншої. У кожній точці лінії напруга змінюється за косинусоїдним законом. Нехай . На такій віддалі від початку лінії амплітуда напруги дорівнює 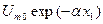; а початкова фаза - 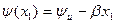. У точці 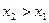амплітуда напруги стане рівною 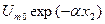, тобто зменшиться в 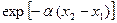разів. Початко­ва фаза 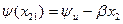за умови 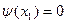визначається за формулою 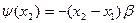. Аналогічно обчис­люються напруга та фаза в точці 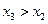. На рис. 8. 9 зображено графіки зміни напруги за часом у точках , які розміщено на різних віддалях від початку лінії. Ці графіки дають наочне уявлення про зміни напруги вздовж лінії за часом.

Розглянемо тепер зміну напруги вздовж лінії для фіксованих моментів часу. Як видно з формули (8.27), напруга вздовж лінії змінюється за косину­соїдним законом з амплітудою, яка зменшується експоненційно. При побу­дові графіків спочатку зображують штриховими лініями обвідну напруги, а потім "вписують" у цю обвідну косинусоїду функцію. Слід зазначити, що нулі функції 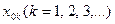збігаються з нулями косинуса, тобто 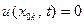, якщо 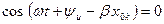. Для додатного 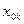це рівняння виконується, якщ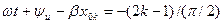о або

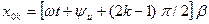. (8.28)

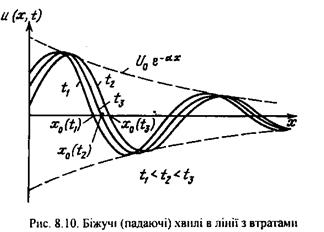
Екстремуми (максимуми та мінімуми) функції 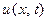не збігаються з екстремумами косинуса і зсунуті відносно останніх дещо ліворуч. На рис. 8.10 зображено згідно з рівнянням (8.27) залежність напруги вздовж лінії для . Даний графік можна інтерпретувати як результат зміни напруги вздовж лінії для заданого моменту. Іншими словами, графік є мовби "фо­тографією" напруги в лінії для моменту .

Але отриманий розподіл напруги не є застиглою картиною. Протягом часу має місце зсув її праворуч. Про­стежимо, наприклад, за зсувом нулів. При з рівняння (8.28) випливає, що , а при 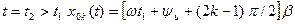. Оскільки , то , тобто нулі зсуваються ліворуч. Цю закономірність відображено на рис. 8.10, де крім розподілу напруги вздовж лінії для 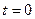подано також розподіли в моменти 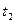та , при цьому .

Таким чином, у лінії виникає хвиля напруги, яка переміщується від поча­тку лінії до її кінця. Така хвиля називається біжучою, або падаючою.

Параметри хвилі. Визначимо параметри хвилі, а саме довжину хвилі , фазову та групову швидкості.

Довжиною хвилі є відстань між двома суміжними точками в напрямі поширення хвилі, фази напруги в яких відрізняються на кут . У точці 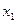фаза напруги . Якщо до 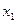добавити , то дістанемо почат­кову фазу . Згідно з визначенням довжини хвилі, різниця 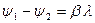має дорівнювати . Звідси

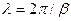. (8.29)

Довжина хвилі не залежить від ослаблення лінії, а повністю визначає­ться коефіцієнтом фази .

Під фазовою швидкістю розуміють швидкість поширення в лінії стану фіксованої фази, наприклад швидкість, з якою перемішується деякий нуль чи максимум вздовж лінії. Обчислюється фазова швидкість при відомих кутовій частоті , коефіцієнті фази (хвильовому числі) за співвідношенням (7.11).

Значно більше практичне значення має так звана групова швидкість, яка ви­значається як швидкість поширення максимуму обвідної групи суміжних за частотою складових складного сигналу. Можна показати, що групова швидкість

.

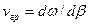Практичне значення групової швидкості обумовлено тим, що з нею тісно пов'язане інше поняття - груповий час. Використовуються також терміни груповий час проходження (ГЧП) та груповий час затримки (ГЧЗ). Груповий час ототожнюється з часом проходження сигналу лінією. Під груповим часом розуміють час пробігу вздовж лінії максимуму обвідної двох суміжних за частотою коливань. Якщо відомий вираз для групової швидкості, то легко записати вираз для групового часу:

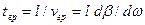. (8.30)

Date: 2016-02-19; view: 478; Нарушение авторских прав