Определение допускаемых напряжений

Основой для расчёта допускаемых напряжений при действии переменных нагрузок служит кривая выносливости (кривая Веллера, рис. 29). Она устанавливает связь между максимальным (предельным) напряжением σ _E, при котором испытывается образец, и заданным числом циклов нагружений N_E до разрушения образца (точка I). Начиная с некоторого напряжения σ _{E lim} (точка II), образец может выдержать бесконечно большое число циклов, не разрушаясь.

Максимальное напряжение, которое образец может выдержать практически неограниченное число циклов, называется пределом выносливости материала σ _{Е lim}. Предел контактной выносливости обозначается с индексом Н - σ _{H lim}, предел выносливости при изгибе с индексом F - σ _{F lim}. Количество циклов нагружений, соответствующее пределу выносливости, называется базовым числом циклов нагружений N_O (при действии контактных напряжений - N_HO, изгибных - N_FO).

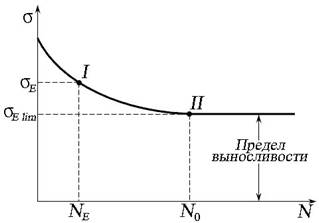
Рис. 29. Кривая выносливости (усталости)

Уравнение наклонного участка кривой выносливости имеет вид:

, откуда . (3.17)

Предельное напряжение при заданном числе циклов нагружений следует из зависимости (3.17):

- предельное контактное напряжение ,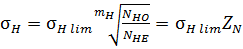

- предельное напряжение при изгибе ,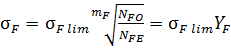

где Z_N и Y_F - коэффициент долговечности при действии контактных и изгибных напряжений соответственно;

m_H и m_F - показатель степени кривой усталости при действии контактных и изгибных напряжений соответственно.

Коэффициент долговечности Z_N и Y_F учитывает влияние срока службы и режим нагрузки передачи (тяжёлый, средний, лёгкий, постоянный):

, m_H = 6, (3.18)

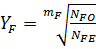, (3.19)

где m_F = 6 с однородной структурой (при улучшении и нормализации);

m_F = 9 при поверхностном упрочнении (закалка ТВЧ, цементация, нитроцементация, азотирование).

Предел контактной выносливости σ _{E lim} и базовое число циклов нагружений N_O зависят от твёрдости рабочих поверхностей (значение твёрдости определяют по табличным данным). Примерное значение N_O можно оценить как:

;

.

Так как большинство зубчатых передач работает в условиях переменных режимов нагрузок, расчёт коэффициентов долговечности ведут по эквивалентному числу циклов перемены напряжений N_HE и N_FE.

Эквивалентным называют такое число циклов перемены напряжений, при котором режим переменной нагрузки эквивалентен постоянному. При постоянной нагрузке, то есть при неизменной частоте вращения зубчатого колеса (n = const):

, (3.20)

где N _∑ - суммарное число циклов нагружений при постоянной нагрузке;

t_h - суммарное время работы зубчатого зацепления в течение года;

k _з - количество контактов одного зуба за один оборот рассчитываемого колеса (обычно k _з = 1).

При переменной нагрузке число циклов нагружений будет эквивалентно числу циклов нагружений при постоянной нагрузке с учётом некоторого коэффициента эквивалентности х _э:

. (3.21)

Пусть при переменной нагрузке в пределах некоторого интервала времени t_i шестерня при n_i = var на различных этапах нагружения передаёт некоторый крутящий момент T_i в пределах этого времени (рис. 30). Тогда суммарное число циклов нагружений за весь срок службы зубчатого зацепления:

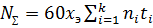, (3.22)

где k - количество переменных нагрузок;

n_i - частота вращения шестерни на i -том участке циклограммы;

t_i - время работы зубчатого зацепления на i -том участке циклограммы.

Рис. 30. Циклограмма нагружения

Из выражений (3.20), (3.21) и (3.22) следует, что коэффициент эквивалентности служит для приведения различных значений крутящего момента к эквивалентному, то есть коэффициент х _э должен учитывать долю крутящего момента по отношению к выбранному эквивалентному моменту (в качестве эквивалентного рекомендуется выбирать максимальный из заданной циклограммы). Если в качестве эквивалентного выбрать максимальный крутящий момент Т ₂ (Т _эк = Т _max = Т ₂), то коэффициент эквивалентности будет равен:

, , , , … ,

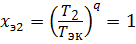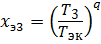(3.23)

где q = 3 - при определении N_HE;

q = (6 … 9) - при определении N_FE.

В соответствии с (3.22) и (3.23), эквивалентное число циклов нагружений при переменной нагрузке будет равно:

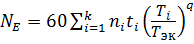. (3.24)

В качестве расчётного крутящего момента выбирают бóльший из действующих в зубчатом зацеплении - крутящий момент на колесе:

, .

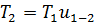В качестве расчётной частоты вращения колеса при определении суммарного числа циклов нагружений выбирают наибольшую - частоту вращения шестерни.

Допускаемое напряжение для зубчатого зацепления определяют с учётом коэффициента запаса прочности по контактным s_H и изгибным s_F напряжениям:

, . (3.25)

Коэффициент запаса прочности S_H = 1,1 - для зубчатых колёс с однородной структурой, S_H = 1,2 - для зубчатых колёс с поверхностным упрочнением. Коэффициент запаса прочности S_F = 1,7.

3.8.3. Проектировочный расчёт зубчатого зацепления

В основе проектировочного расчёта лежит расчёт на прочность зубчатого зацепления. Расчёт связан с определением основных параметров зацепления - межосевого расстояния а_ω и нормального модуля зацепления m_n. Межосевое расстояние определяют, исходя из выносливости по контактным напряжениям. Модуль определяют исходя из расчёта по напряжениям изгиба. Значение межосевого расстояния а_ω и модуля зацепления m_n, получаемые из прочностного расчёта, округляют в соответствии с ГОСТом до ближайшей бóльшей величины.

При работе зубчатой передачи между зубьями сопряжённых зубчатых колёс возникает сила давления F_n, действующая по линии зацепления. В результате действия силы F_n в теле зуба колеса возникают контактные напряжения σ _H и напряжения изгиба σ _F (рис. 31).

Контактные напряжения σ _H вызывают выкрашивание поверхностных слоёв зубьев, напряжения изгиба σ _F - поломку зубьев.

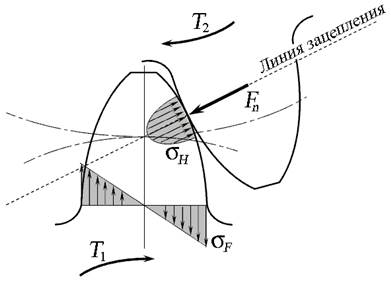
Рис. 31. Контактные σ _H и изгибные σ _F напряжения,

возникающие от действия силы F_n

В основе расчёта контактных напряжений, имеющих максимальное значение в полюсе на линии контакта поверхностей зубьев колёс, используют формулу Герца:

, (3.26)

где Z_E - коэффициент, учитывающий механические свойства материала шестерни и колеса (упругость материала, определяемое модулем упругости, и поперечное сжатие, определяемое коэффициентом Пуассона);

F_n - сила, действующая в зацеплении по нормали к линии зуба;

ρ _пр - приведённый радиус кривизны контактирующих поверхностей;

l _∑ - суммарная длина контактных линий;

- нормальная нагрузка на единицу длины контактной линии.

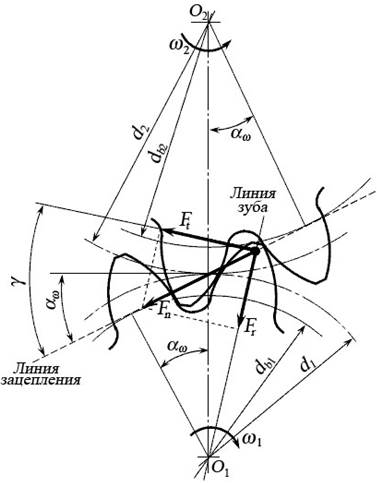
При определении изгибных напряжений зуб рассматривают как консольную балку, причём наибольшие напряжения изгиба возникают в случае, если нормальная сила F_n приложена к вершине зуба (рис. 32, а). Независимо от того, сколько пар зубьев находятся в зацеплении, принимают, что вся нагрузка воспринимается одним зубом. Силу F_n переносят по линии её действия и прикладывают к оси зуба (точка О), раскладывая её при этом на две составляющие - окружную F_t и радиальную F_r:

, (3.27)

. (3.28)

а) б)

Рис. 32. Схема к расчёту прочности зубьев на изгиб

Угол γ несколько больше угла зацепления α_ω, так как при расположении вершины зуба на линии зацепления ось зуба не совпадает с линией центров О ₁ О ₂ (рис. 32, б). Наибольшее напряжение возникает у ножки зуба в зоне перехода эвольвенты в галтель (сечение АВ). За расчётное напряжение принимают напряжение на растянутой стороне зуба (точка В), так как именно здесь возникают трещины усталостного разрушения:

σ _F = σ_из – σ_сж. (3.29)

Напряжения изгиба и сжатия в опасном сечении АВ, возникающие от действия сил F_t и F_r:

, , (3.30)

где - изгибающий момент от действия силы окружной F_t;

h_p - плечо силы F_t относительно опасного сечения;

s_t - толщина зуба;

W_x - осевой момент сопротивления опасного сечения ножки зуба.

Расчётное напряжение изгиба σ _F определяют с учётом коэффициента концентрации напряжения k_σ:

. (3.31)

При проектировочном расчёте значение допускаемого напряжения выбирают мéньшее из допускаемых напряжений для шестерни и колеса.

3.8.4. Проверочный расчёт

Проверочный расчёт зубчатых зацеплений проводят по контактным и изгибным напряжениям при перегрузках. Работоспособность передачи по контактным напряжениям определяют при выполнении условия:

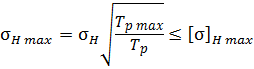, (3.32)

где T_p и T_{p max} - расчётный и максимальный пиковый момент, действующий в зацеплении;

- предельное допускаемое контактное напряжение.

Максимальный пиковый момент определяют с учётом коэффициента динамичности K_d = 1,5 … 2,5, или принимают равным максимальному вращающему моменту электродвигателя с учётом соответствующего передаточного отношения и КПД зубчатого зацепления.

Предельное допускаемое напряжение принимают в зависимости от способа химико - термической обработки:

- при нормализации, улучшении и объёмной закалке = 2,8σ_т;

- при цементации = 44 Н_HRC;

- при азотировании = 3 H_HV.

Прочность зуба, необходимую для предотвращения остаточных деформаций, хрупкого излома или образования первичных трещин в поверхностном слое, возникающих при перегрузках, определяют по условию:

, (3.33)

где - максимальное напряжение при изгибе;

- предельное допускаемое напряжение при изгибе.

Максимальное расчётное напряжение при изгибе определяют аналогично расчёту контактного напряжения:

. (3.34)

Ориентировочно можно принимать ≈ 0,8σ_т при Н_НВ < 350, и ≈ 0,6σ_т при Н_НВ > 350 (σ_т - предел текучести материала).

3.9. Особенности расчёта косозубых цилиндрических передач

Для расчёта косозубых цилиндрических передач используют те же формулы, что и для прямозубых, с той лишь разницей, что для расчёта контактных и изгибных напряжений некоторые коэффициенты имеют свои значения вследствие угла наклона зуба колеса β. В отличие от прямозубых передач, в которых одна пара зубьев сопрягаемых колёс входит в зацепление сразу по всей длине зуба, в косозубых передачах в зацеплении участвуют несколько пар зубьев.

С увеличением угла β наклона линии зуба будет расти осевая сила , наличие которой требует осевую фиксацию вала, что приводит к усложнению конструкции опор валов и применению более дорогих радиально - упорных подшипников. Поэтому угол наклона β в большинстве случаев ограничивают значениями β = 8 … 22°.

Прочность зуба при изгибе косозубого колеса определяется его размерами и формой в нормальном сечении. Известно, что профиль зуба косозубого колеса в нормальном сечении совпадает с профилем зуба прямозубого колеса. В соответствии с этим расчёт косозубых колёс ведут, используя параметры эквивалентного прямозубого колеса.

Эквивалентным называют такое прямозубое колесо, прочность зуба которого соответствует прочности зуба косозубого колеса. Параметры эквивалентного колеса обозначают индексом - υ.

Начальная окружность косозубого колеса в нормальном сечении (сечение А - А, рис. 33) представляет собой эллипс с полуосями е и с, значение которых, исходя из геометрических построений, будут равны:

, . (3.35)

Рис. 33. Схема к определению эквивалентного числа зубьев

Максимальный радиус кривизны ρ_υ определяется по формуле из аналитической геометрии:

. (3.36)

Эквивалентный делительный диаметр d_υ равен двум радиусам кривизны ρ_υ:

, (3.37)

откуда эквивалентное число зубьев ,

. (3.54)

Увеличение эквивалентных параметров (ρ_υ, d_υ и z_υ) с увеличением угла β наклона зуба косозубого колеса при неизменных параметрах косозубого колеса (d и z) является одной из причин повышения прочности косозубых передач. Для косозубого колеса эквивалентным будет прямозубое колесо бóльших размеров, поэтому применение косозубого колеса уменьшает габариты передачи.

Планетарные передачи

Date: 2016-02-19; view: 3165; Нарушение авторских прав