Параметры зубчатого зацепления

Для пары зацепляющихся колёс (рис. 12) окружной шаг зацепления р_t, измеренный по дуге делительной окружности диаметром d (для колёс, выполненных без смещения, диаметры делительной и начальной окружностей совпадают - d_ω = d) между одноимёнными профилями соседних зубьев, должен быть одинаков. Очевидно, что πd = p_t z (z - число зубьев колеса), откуда:

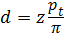. (3.1)

Отношение 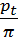является основным расчётным числом зубчатых передач, которое называется модулем m, единицей измерения которого является миллиметр. Модуль - это часть диаметра делительной окружности, приходящейся на один зуб:

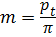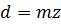, . (3.2)

Модуль - основная характеристика зубьев, стандартизирован. Согласно ГОСТ 13755 - 81, высота головки зуба h_a = m, h_f = 1,25 m.

Рис. 12. Элементы зубчатого зацепления

Основными геометрическими элементами цилиндрического эвольвентного прямозубого зацепления являются:

- диаметр окружности впадин ;

- диаметр основной окружности ;

- диаметр делительной (начальной) окружности d (d_ω);

- диаметр окружности выступов

;

- угол зацепления α_tω (для передач, выполненных без смещения исходного контура, α_tω = α_t = α = 20 °);

- межосевое расстояние .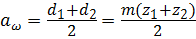

Рис. 13. Схема взаимодействия зубьев колёс по длине

контактной линии АВ

Передача крутящего момента в процессе вращения пары зубчатых колёс происходит при взаимодействии зубьев колёс по линии АВ, называемой контактной линией (рис. 13), которая перемещается вдоль линии зацепления при непосредственном контакте зубьев от точки 1 до точки 2.

Для обеспечения непрерывной безударной работы необходимо, чтобы вход в зацепление каждой пары зубьев происходил несколько раньше, чем выход предыдущей пары. Это свойство зубчатых передач характеризуется коэффициентом перекрытия. Прямозубые передачи характеризуются коэффициентом торцового перекрытия.

Коэффициент торцового перекрытия зубчатой передачи ε_α - это отношение угла торцового перекрытия к его угловому шагу, измеренному по дуге основной окружности:

.

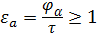Коэффициент торцового перекрытия прямозубых передач выбирают в пределах ε_α = 1,05 … 1,2 (значение ε_α = 1,05 считается минимально допустимым при проектировании передачи).

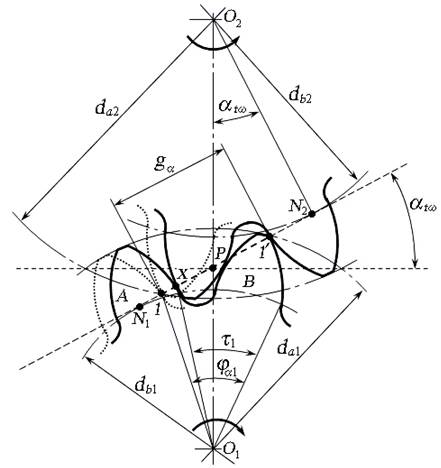
Рис. 14. Схема к определению коэффициента торцового перекрытия

Угол торцового перекрытия φ_α - это угол поворота колеса по дуге основной окружности от положения зуба при входе в зацепление (зуб А входит в зацепление в точке 1, рис. 14), до положения этого же зуба при выходе из зацепления в точка 1 ′.

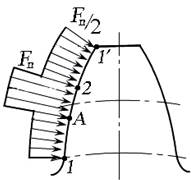
Рис. 15. Схема зон перекрытия по контактной линии:

g_α - длина активной линии зацепления; p_t - нормальный шаг зацепления;

b_ω - ширина зубчатого колеса; F_n - передаваемое усилие

При вращении колёс контактная линия перемещается в поле зацепления со сторонами g_α и b_ω (рис. 15). Контактная линия 1 при зацеплении пары зубьев колёс перемещается вдоль линии зацепления до выхода из зацепления этой пары до положения 1 ′. Последующая пара зубьев колёс до выхода из зацепления первой пары образует зацепление по контактной линии 2, передавая усилие F_n одновременно с первой парой. По линии А предыдущая пара выходит из зацепления, и на участке А - 2 усилие передаётся только одной парой зубьев. Коэффициент торцового перекрытия будет равен:

.

Так как для определения коэффициента ε _α по этой формуле необходима геометрическая зарисовка зацепления, то для определения коэффициента используют различные математические формулы для зубчатого зацепления, выполненного без смещения или со смещением исходного контура.

Смещение исходного контура (модификацию или коррегирование) выполняют при числе зубьев шестерни менее z < 17, а также для того, чтобы «вписать» зубчатые передачи в единое межосевое расстояние (например, в ступенчатых коробках передач) или увеличить прочность шестерни и (или) колеса. При модификации профиля можно уменьшить минимальное количество зубьев в среднем до z_min = 12 … 14 и меньше. Различают угловую и высотную коррекцию.

Угловая коррекция заключается в смещении профиля зубьев малой шестерни от центра (в плюс). При этом на величину xm увеличиваются диаметры основных окружностей (если х _∑ > 0), следовательно, увеличивается и угол зацепления α_tω, увеличение которого в свою очередь повышает контактную прочность (можно увеличить α_tω с 20 до ≈ 25° и увеличить допустимую нагрузку до 20 %). При угловой коррекции сумма коэффициентов смещения шестерни х ₁ и колеса х ₂ не равна нулю (х _∑ = х ₁ + х ₂ ≠ 0).

Так как угловая коррекция приводит к увеличению межосевого расстояния (при х _∑ > 0), то это приведёт к уменьшению коэффициента торцового перекрытия меньше единицы (ε _α < 1), что в свою очередь приведёт к образованию разрыва в зацеплении. Поэтому межосевое расстояние увеличивают на мéньшую величину у = х ₁ + х ₂ – ∆ у (∆ у - коэффициент уравнительного смещения).

При высотной коррекции положительное смещение для шестерни совмещают с равнозначным по модулю отрицательным смешением, то есть шестерня упрочняется по изгибу за счёт колеса (х ₁ = х ₂, х _∑ = 0). Высотную коррекцию применяют при больших передаточных числах и малых числах зубьев шестерни. Изменение профиля зуба колеса при различном смещении исходного контура изображено на рис. 16.

а) б)

Рис. 16. Смещение исходного контура:

а) - профиль зуба при различных числах зубьев колеса n;

б) - профиль зубьев колеса при положительном смещении:

d и d_ω - делительный и начальный диаметры; xm_n - величина смещения;

m_n - нормальный модуль

Date: 2016-02-19; view: 3303; Нарушение авторских прав