Закрепление усвоенных навыков и умений учащихся

Задача 1. Найдите углы параллелограмма ABCD (рис. 2).

Решение

Так как AB ǁ CD и AC — секущая, то ∠ ACD =∠ BAC =40º.

А т. к. BC ǁ AD и AC — секущая, то ∠ CAD =∠ BCA =35º. Таким образом, ∠ A =∠ C =35º+40º=75º. По свойству углов, прилежащих к одной стороне параллелограмма, ∠ A +∠ B =180º, отсюда ∠ B =180º−∠ A =180º−75º=105º. По свойству противолежащих углов параллелограмма ∠ D =∠ B =105º.

Ответ: 75º, 75º, 105º, 105º.

Задача 2. Точка пересечения диагоналей параллелограмма удалена от двух его вершин на 3 см и 5 см. Найдите диагонали параллелограмма.

Решение

Из условия задачи и свойства диагоналей параллелограмма следует, что в условии речь идет о соседних вершинах параллелограмма.

Т.е. 3 см и 6 см — это половины диагоналей. Значит, диагонали равны 6 см и 10 см.

Ответ: 6 см, 10 см.

Задача 3. Периметр параллелограмма ABCD равен 10 см. Найдите

длину диагонали BD, если периметр треугольника ABD равен 8 см.

Решение

Из свойства противолежащих сторон параллелограмма и условия следует, что AB + AD =10:2 =5 (см). Т.к. P _{Δ ABD} = AB + AD + BD =8 см, то BD =8−5 =3 (см).

Ответ: 3 см.

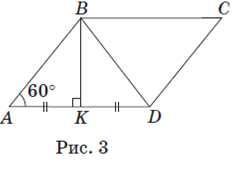
Задача 4. В параллелограмме ABCD ∠ A =60º, высота BK делит сторону AD на две равные части. Найдите длину диагонали BD, если периметр параллелограмма равен 48 см.

Решение

Пусть на рис. 3 AK = KD = x см. В прямоугольном треугольнике ABK (∠ AKB =90º) ∠ ABK =90º−60º=30º. Как известно, в прямоугольном треугольнике против угла в 30ºлежит катет, равный половине гипотенузы.

D

Значит, AB =2⋅ AK =2 x (см).

P _ABCD = AB+BC+CD+AD = 2 x ⋅4=8, 8 x =48, x =6. Следовательно,

AB = BC = CD = AD =6⋅2 =12 (см). Рассмотрим треугольник ABD. Это

равнобедренный треугольник с основанием AD, так как высота BK

является его медианой. Значит, BD = AB =12 см.

Ответ: 12 см.

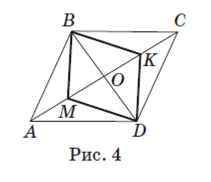
Задача 5. В параллелограмме ABCD (рис. 4) на диагонали AC отложены равные отрезки AM и CK. Докажите, что четырехугольник

BMDK — параллелограмм.

Доказательство

Проведем диагональ BD. По свойству диагоналей параллелограмма диагонали BD и AC пересекаются в точке O и делятся ею пополам:

BO = OD, AO = CO. Т.к. AM = CK, то OM = OK. Значит, в четырехугольнике BMDK диагонали пересекаются и делятся точкой пересечения пополам. Следовательно, четырехугольник BMDK —параллелограмм по признаку.

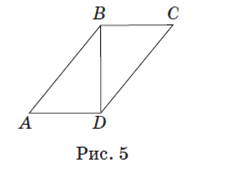
Задача 6. Периметр параллелограмма равен 90 см, его острый

угол равен 60º. Диагональ параллелограмма делит его тупой угол в отношении 1: 3. Найдите стороны параллелограмма.

Решение

Пусть в параллелограмме ABCD (рис. 5) ∠ A =60º BD — диагональ параллелограмма, ∠ ABD:∠ CBD =1:3. Т.к. по свойству

углов, прилежащих к одной стороне параллелограмма, их сумма

равна 180º, то ∠ A +∠ B =180º, значит, ∠ B =180º−∠ A =180º−60º=120º. Пусть ∠ ABD = x, тогда ∠ CBD =3 x. Отсюда x +3 x =120, 4 x =120, x =30. Таким образом, ∠ ABD =30º, ∠ CBD =90º. Следовательно, треугольник ABD — прямоугольный, ∠ ADB =90º. Т. к. AD — катет, лежащий против угла в 30º, то AB =2 AD. Поскольку P_ABCD =90 см, то, используя свойство противолежащих сторон параллелограмма, получим: (AD +2 AD)⋅2 =90, 3⋅ AD =45, AD =15 (см).

Следовательно, BC = AD =15 см. Тогда AB = CD =2⋅15 =30 (см).

Ответ: 15 см, 15 см, 30 см, 30 см.

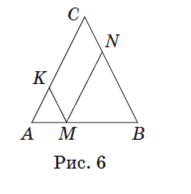
Задача 7. На стороне AB равностороннего треугольника ABC выбрана точка M (рис. 6). Через точку M проведены отрезки MK и MN, параллельные сторонам BC и AC соответственно. Найдите сторону треугольника ABC, если периметр параллелограмма MKCN равен 60 см.

Решение

Т.к. треугольник ABC — равносторонний, то ∠ A =∠ B =∠ C =60º. Т. к. AC ǁ MN по условию, тогда ∠ A =∠ NMB как соответственные углы при параллельных прямых AC и MN и секущей AB. Таким образом, в треугольнике MNB ∠ NMB =∠ B =60º. Значит, треугольник MNB — равносторонний, MB =MN = NB. Аналогично доказываем, что треугольник AKM — равносторонний, AK = KM = AM.

Т. к. по условию P_MKCN =60 см, то CK + KM =30 (см). Поскольку KM = AK, то CK+AK =30 (см). Т.е. AC =30 см. Значит, AC = BC = AB =30 см.

Ответ: 30 см.

Date: 2015-04-23; view: 572; Нарушение авторских прав