Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Метод термодинамических циклов
|
|
Круговым циклическим процессом называют процесс, в котором термодинамическая система, пройдя ряд состояний, возвращается в исходное состояние, При этом возможно неоднократное повторение соответствующих преобразований, каждое из которых представляет собой замкнутый цикл. Практически все тепловые двигатели работают с использованием тех или иных циклов. Существенным для работы двигателя, преобразующего тепловую энергию в работу является то, что находящееся в двигателе рабочее упругое тело (газ) обязательно контактирует с, так называемым, нагревателем, получая от него теплоту (Q н) и холодильником, которому рабочее тело отдает часть тепла (Q х). Таким образом, полное превращение тепла в работу невозможно.
Исследование закономерностей работы тепловых двигателей на основе количественного анализа термодинамических процессов, составляющих замкнутый цикл конкретного типа теплового двигателя, проводится с использованием метода термодинамических циклов. Циклы, рассматриваемые в данном методе, составляются из равновесных частных термодинамических процессов, моделирующих реальную работу двигателя. Такой анализ позволяет выявить наиболее эффективные условия превращения тепла в работу.
2.1. Цикл Карно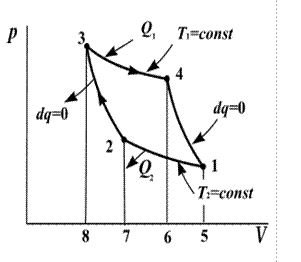 
Цикл Карно начинается с изотермического процесса 3®4 в котором, получивший от нагревателя теплоту (Q н) газ расширяется, производя работу. Затем, контакт с нагревателем прерывается, но газ продолжает расширяться 4®1 в адиабатических условиях.
В состоянии 1 газ приводится в контакт с холодильником и отдает ему теплоту (Q х).
При этом, вследствие инерционности двигателя и присоединенных движущихся деталей поршень начинает сжатие газа 1®2. Процесс сжатия продолжается и дальше 2®3, но уже адиабатно, без теплового контакта с холодильником. Затем цикл повторяется (рисунок 2.1).
Итак, цикл Карно состоит из следующих термодинамических процессов: изотермического 3®4; адиабатического 4®1; изотермического 1®2 и адиабатного 2®3.
При количественном анализе цикла Карно необходимо обращаться к формулам и определениям, рассмотренным нами ранее в разделе 1.
Так, для изотермического процесса 3®4:
Q н = L 3®4 = (М /μ) RТ н.ln(V 4/ V 3), (2.1.1)
а для изотермического процесса 1®2:
Q х = L 1®2 = (М /μ) RТ хln(V 2/ V 1). (2.1.2)
Полезная работа цикла определяется алгебраической суммой: L0 = L 3®4 + L 1®2. С другой стороны, полезная работа совершается за счет алгебраической суммы теплот L 0 = Q н + Q х. Таким образом, энергетический баланс запишется в виде:
Q н + Q х = L 3®4 + L 1®2 = (М /μ) R (Т н ln(V 4/ V 3) - Т х ln(V 1/ V 2). (2.1.3)
Используя уравнения адиабаты, для точек 4 и 1: р 4 V 4 k = р 1 V 1 k и для точек 2, 3: р 3 V 3 k = р 2 V 2 k, применяя так же уравнения изотерм: р 3 V 3 = р 4 V 4 (3®4) и р 1 V 1 = р 2 V 2 (1®2), найдем соотношение: V 4/ V 3 = V 1/ V 2. Последнее позволит упростить уравнение (2.1.3):
Q н + Q х = (М /μ) R (Т н - Т х)ln(V 4/ V 3). (2.1.4)
Последняя формула позволит определить термический коэффициент полезного действия цикла Карно (h). Согласно определению, он равен отношению полезно затраченной теплоты ко всей исходной теплоте процесса:
h = (Q н + Q х)/ Q н.
Подставляя в определительное уравнение для h выражения из формул (2.1.4) и (2.1.1) найдем:
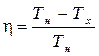(2.1.5)
К.П.Д. цикла Карно с идеальным газом зависит только от абсолютных температур нагревателя и холодильника.
Date: 2015-05-22; view: 657; Нарушение авторских прав