Связь многогранников с живой природой (Слайд № 20, 21, 22)

Рассуждая об устройстве мира, нельзя оставить без внимания живую природу. Встречаются ли в живой природе правильные многогранники?

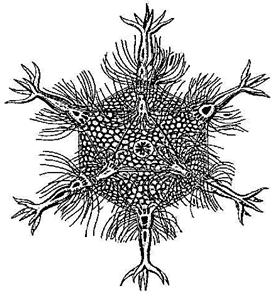
1. Правильные многогранники встречаются и в живой природе. Например, скелет одноклеточного организма феодарии (Circogonia icosahedra) по форме напоминает икосаэдр. Большинство феодарий живут на морской глубине и служат добычей коралловых рыбок. Но простейшее животное пытается себя защитить: из 12 вершин скелета выходят 12 полых игл. На концах игл находятся зубцы, делающие иглу еще более эффективной при защите.

Чем же вызвана такая природная геометризация феодарий? Тем, по-видимому, что из всех многогранников с тем же числом граней именно икосаэдр имеет наибольший объем при наименьшей площади поверхности. Это свойство помогает морскому организму преодолевать давление водной толщи.

2. Интересно, что икосаэдр оказался в центре внимания биологов в их спорах относительно формы некоторых вирусов. Вирус не может быть совершенно круглым, как считалось раньше. Для того чтобы определить его форму, брали разные многогранники, направляли на них свет под теми же углами, что и поток атомов на вирус. Оказалось, что только один многогранник дает точно такую же тень – икосаэдр.

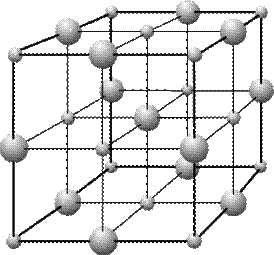
3. Правильные многогранники – самые выгодные фигуры. И природа этим широко пользуется. Подтверждением тому служит форма некоторых кристаллов. Взять хотя бы поваренную соль, без которой мы не можем обойтись. Известно, что она хорошо растворима в воде, служит проводником электрического тока. А кристаллы поваренной соли (NaCl) имеют форму куба.

4. При производстве алюминия пользуются алюминиево-калиевыми квасцами (K[Al(SO₄)₂]·12H₂O), монокристалл которых имеет форму правильного октаэдра.

5. Получение серной кислоты, железа, особых сортов цемента не обходится без сернистого колчедана (FeS). Кристаллы этого химического вещества имеют форму додекаэдра.

6. В разных химических реакциях применяется сурьмянистый сернокислый натрий (Na₅(SbO₄(SO₄)) – вещество, синтезированное учеными. Кристалл сурьмянистого сернокислого натрия имеет форму тетраэдра.

7. Последний правильный многогранник – икосаэдр передает форму кристаллов бора (B). В свое время бор использовался для создания полупроводников первого поколения.

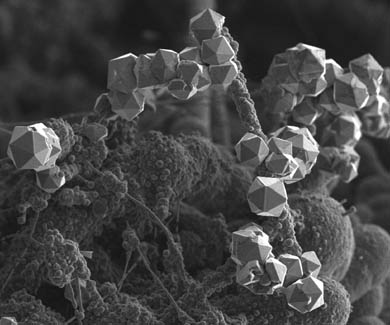
Итак, благодаря правильным многогранникам, открываются не только удивительные свойства геометрических фигур, но и пути познания природной гармонии.

Заключение.

В ходе работы над рефератом я изучил правильные многогранники, рассмотрел их модели, выделил и систематизировал свойства каждого из многогранников. Кроме этого я узнал, что правильные многогранники с древних времен привлекали внимание ученых, строителей, архитекторов и многих других. Их поражала красота, совершенство, гармония этих многогранников. Пифагорейцы считали эти многогранники божественными и использовали их в своих философских сочинениях о существе мира. Подробно описал свойства правильных многогранников древнегреческий ученый Платон. Правильным многогранникам посвящена последняя XIII книга знаменитых «Начал» Евклида. К многогранникам обращались и в более позднее время. Это видно из научных трудов Иоганна Кеплера.

Я решил выполнить презентацию, используя знания, полученные на уроках математики и информатики. Мне хотелось создать такую презентацию, чтобы ее можно было использовать на уроках геометрии. Весь материал реферата не имеет смысла отражать в слайдах, поэтому я выбрал, на мой взгляд, самое важное. Для большей наглядности использовал рисунки, фотографии, таблицы.

Работа мною выполнена в 2-х вариантах: печатном и электронном, предусмотрена возможность показа презентации «Правильные многогранники» при помощи мультимедийной установки.

Помимо специальной литературы я использовал возможности INTERNET.

Презентация создана с помощью программы Microsoft Power Point, содержит 23 слайда.

Литература.

1. Учебник. Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. Геометрия, 10-11

классы.

2. Пособие для поступающих в вузы.Кутасов А.Д., Пиголкина Т.С. и др.. М., «Наука», 1985.

3. Информатика: Лабораторный практикум. Создание текстовых документов в текстовом редакторе Microsoft Word 2000/ Авт.-сост. В.Н. Голубцов, А.К.Козырев и др., Саратов: Лицей, 2003.

4. Сборник конкурсных задач по математике для поступающих в вузы под ред. Сканави М.И., Санкт-Петербург, 1994.

5. Интернет – сайты.

6. Гросман С., Тернер Дж. Математика для биологов. М., 1983.

7. Курант Р., Роббинс Г. Что такое математика? М., 1967.

8. Кованцов Н.И. Математика и романтика. Киев, 1976.

9. Кокстер Г.С.М. Введение в геометрию. М., 1966.

10. Смирнова И.М. В мире многогранников. М., 1990.

11. Шарыгин И.Ф., Ерганжиева Л.Н. Наглядная геометрия. М., 1992.

12. Энциклопедический словарь юного математика. М., 1989.

ПРИЛОЖЕНИЕ

5.1. Определение правильного многогранника (Слайд № 7).

Многогранник называется правильным, если:

он выпуклый,

все его грани - равные правильные многоугольники,

в каждой вершине сходится одинаковое число граней,

все его двухгранные углы равны.

5.2. Тетраэдр и его свойства (Слайд № 8, 9).

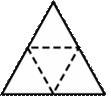
n Тетраэдр составлен из четырех равносторонних треугольников.

n Каждая его вершина является вершиной трех треугольников.

n Сумма плоских углов при каждой вершине равна 180 градусов.

Date: 2015-04-23; view: 1671; Нарушение авторских прав