Доказательство существования пяти правильных многогранников

Зададимся вопросом о том, сколько правильных многогранников существует?

Предположим, что правильный многогранник имеет

Г граней, из которых каждая есть правильный n-угольник,

у каждой вершины сходятся k ребер,

всего в многограннике В вершин и Р ребер,

причем n 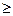3, поскольку у каждой вершины сходится не менее трех сторон,

и k 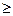3, поскольку у каждой вершины сходится не менее трех ребер.

Считая ребра по граням, получим: n Г = 2Р.

Каждое ребро принадлежит двум граням, значит, в произведении

n Г число Р удвоено.

Считая ребра по вершинам, получим: k 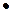В = 2Р, поскольку каждое ребро упирается в 2 вершины. Тогда равенство Эйлера дает:

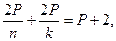или . (*)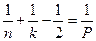

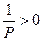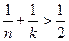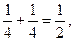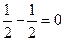По условию , тогда , т.е. n и k не могут быть более трех. Например, если бы было n = 4 и k = 4, то тогда и 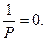Прикидкой можно проверить, что и другие значения n и k, большие 3, не удовлетворяют равенству (*). Значит, либо k = 3, либо n = 3.

Пусть n = 3, тогда равенство (*) примет вид:

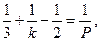или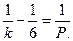

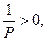
Поскольку 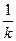может принимать значения , ,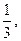

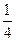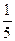т.е. k = 3, 4, 5.

Если k = 3, n = 3, то P = 6, Г = 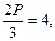В = 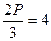- это тетраэдр (см. табл. 1).

Если k = 4, n = 3, то Р = 12, Г = 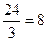, В = 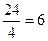- это октаэдр.

Если k = 5, n = 3, то Р = 30, Г = 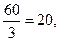В = 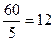- это икосаэдр.

Пусть теперь k = 3, тогда равенство (*) примет вид:

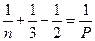, или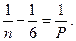

Отсюда следует, что n может принимать значения 3, 4, 5.

Случай n = 3 разобран.

Остаются два случая:

n = 4 при k = 3, тогда 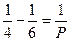, т.е. Р = 12, Г = 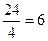, В = 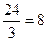- это куб.

n = 5 при k = 3, тогда 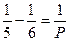, Р = 30, Г = 12, В = 30 - это додекаэдр.

Мы доказали, что существует пять и только пять правильных выпуклых многогранников. Доказательство того, что больше не может быть, содержится в «Началах» Эвклида, причем автором этого доказательства считается Теэтет. Известно, что в течение нескольких лет Теэтет состоял в Академии и был близок к Платону, и этой близостью можно объяснить то обстоятельство, что Платон оказался знакомым с новейшими в то время открытиями в области стереометрии.

Date: 2015-04-23; view: 1884; Нарушение авторских прав