
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Приближенные построения разверток
|
|
Развертку неразвертывающихся поверхностей вращения строят приближенно.
1. СПОСОБ ЦИЛИНДРОВ. Способ состоит в том, что данную поверхность вращения разбивают с помощью меридианов на сравнительно узкие, равные между собой доли. Каждую такую долю заменяют описанной цилиндрической поверхностью, которая касается данной поверхности в точках среднего меридиана доли. Этот средний меридиан будет вместе с тем нормальным сечением цилиндрической поверхности. Границами цилиндрической поверхности будут плоскости меридианов, ограничивающих рассматриваемую долю.
Пример. Построить развертку данной сферы (рис. 169). Разобьем сферу при помощи меридианов на шесть равных частей. Рассмотрим построение приближенной развертки одной части сферы, средним меридианом которой является главный меридиан f.
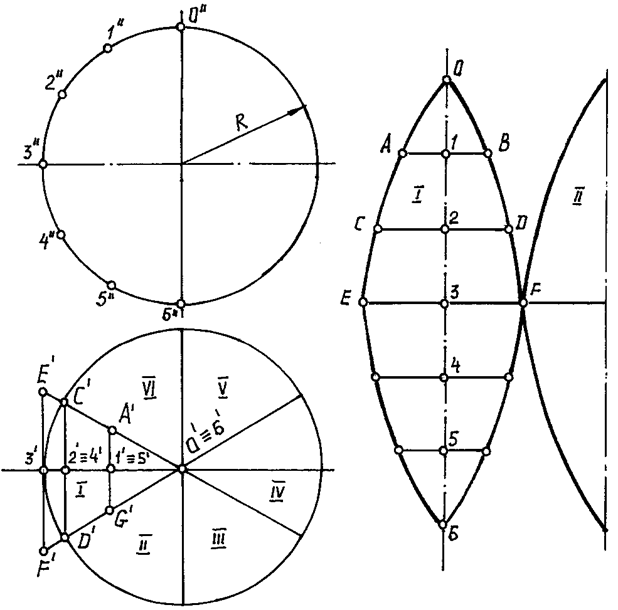
| Рис. 169 |
Прежде всего заменим эту часть сферы цилиндрической поверхностью, описанной около нее. Образующие этой поверхности будут фронтально проецирующими прямыми и поэтому проецируются в натуральную величину на горизонтальную плоскость проекций H. Нормальным сечением цилиндрической поверхности будет половина главного меридиана f, а границами поверхности будут плоскости меридианов, ограничивающих рассматриваемую часть.
Для построения развертки этой цилиндрической поверхности заменяем ее вписанной призматической поверхностью. Для этого делим половину главного меридиана на шесть равных частей и через точки деления проводим образующие цилиндрической поверхности. Затем спрямляем полумеридиан f в отрезок прямой и через его точки деления проводим перпендикулярно к нему образующие EF = EF = E1F1, CD = CD = C 1 D 1 и т.д.
Соединив концы этих образующих плавными кривыми, получим приближенную развертку одной доли данной сферы, равной 1/6 ее части. Развертки остальных долей являются повторением первой.
Обычно сферу разбивают на двенадцать и более частей для получения более точной ее развертки.
2. СПОСОБ КОНУСОВ. Этот способ состоим в замене неразвертывающихся поверхностей такой другой поверхностью, которая составлена из нескольких конических и, следовательно, развертываемых элементов.
Построение развертки способом конусов показано на примере поверхности вращения произвольного вида (рис. 170).
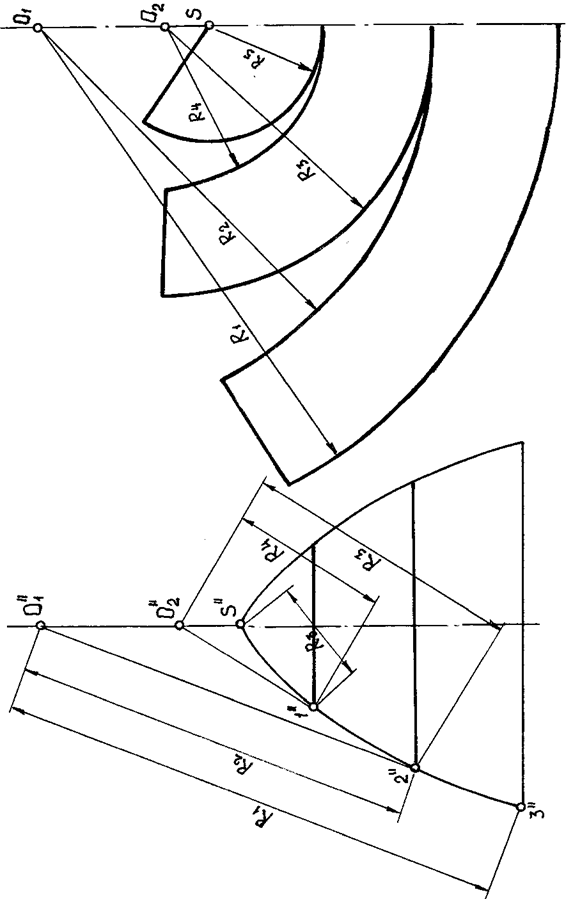
| Рис. 170 |
Разделим данную поверхность на несколько поясов, проходящих через точки 1(1”), 2(2”), 3(3”) главного меридиана (рис.).
Каждый из трех выделенных поясов заменим конусом: первый и второй — описанным около данной поверхности, а третий — вписанным в эту поверхность (рис. 170).
Построение приближенной развертки заданной поверхности сводится к построению разверток трех конусов.
Границами между отдельными частями развертки являются параллели развертываемой поверхности вращения, переходящие в дуги окружностей, которые должны совпадать. Так, длины дуг, имеющих радиусы R 2 и R 3 и радиусы R 4 и R 5, попарно равны и могут легко определяться построением, как показано на рис. 109.
Date: 2015-04-23; view: 954; Нарушение авторских прав