Закон сохранения энергии в движущемся воздухе. Выведите уравнение Бернули и дайте ему пояснение

Движение воздуха по шахтным выработкам подчи­няется общим законам аэродинамики: воздух всегда движется из пространства с большим давлением в сто­рону пространства с меньшим давлением.

БЕРНУЛЛИ УРАВНЕНИЕ, связывает скорость и давление в потоке идеальной несжимаемой жидкости при установившемся течении. Бернулли уравнение выражает закон сохранения энергии движущейся жидкости..

Основным уравнением движения воздуха по руднич­ным выработкам является уравнение Бернулли, кото­рое, применительно к шахтным условиям, имеет вид

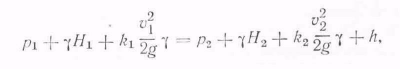
где p₁ и р₂ — статические давления в начальном и ко­нечном сечениях потока;

H₁ и H₂ — высота расположения сечений потока воз­духа над произвольно выбранной горизон­тальной плоскостью, принятой за плос­кость сравнения;

k₁ и k₂ — коэффициенты кинетической энергии, учи­тывающие неравномерность распределения скоростей в начальном и конечном сече­ниях потока;

v₁ и v₂ — средние скорости движения воздуха в на­чальном и конечном сечениях потока;

h — потеря давления на преодоление сопро­тивлений при движении воздуха отначального сечения к конечному.

Уравнение Бернулли выражает закон сохранения энергии, поскольку сумма энергий в различных сечени­ях потока одинакова в идеальных потоках, а в реальных потоках сумма энергий в сечении II в направлении дви­жения потока меньше суммы энергий в сечении I потока на величину h_1-2 потерь энергии на преодоление сопротивления движению текущей среды и эта потерянная энергия превращается в тепло, рассеиваемое в потоке.

Уравнение Бернулли для потока воздуха в шахтной вентиляционной сети с учетом того, что коэффициенты k₁ и k₂ близки к единице, а величины H₁ и H₂ равны вертикальной высоте столба воздуха, примет следующий вид:

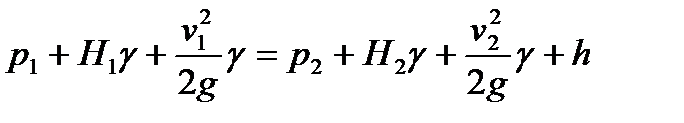, кг/м².

Отсюда находим величину суммарных потерь энер­гии потока при перемещении его от сечения S₁ к сече­нию S₂:

h=(p₁-p₂)+(H₁-H₂)γ+ 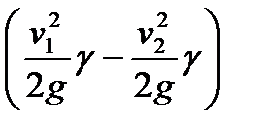, кг/м².

Заменив в этом выражении слагаемые (р₁ — p₂) величиной h_1-2, 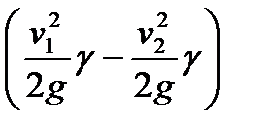величиной h_v и (H₁-H₂) величиной h_e, получим

h = h_l-₂+h_v±h_e, кг/м²,

где h_l-₂ - потери статического давления воздуха на участке между сечениями S₁ и S₂, кг/м²; h_v — разность скоростных давлении воздуха между рассматриваемыми сечениями, кг/м²; h_е — естественная тяга воздуха (знак «+» ставится, если естественная тяга действует против потока, и «—», если она действует в направлении обще­го потока), кг/м²

Date: 2015-05-22; view: 1111; Нарушение авторских прав