Пояснения к выполнению эпюра 2

(нахождение истинной величины сечения способом замены плоскостей проекций)

Задача 1

В первой задаче данного примера требуется построить линию пересечения пирамиды с плоскостью, заданной следами, а также определить видимость пирамиды относительно секущей плоскости, а также секущей плоскости относительно пирамиды.

Этап 1 (рис.15). Решение задачи начнем на горизонтальной плоскости проекций. Здесь к горизонтальному следу заданной плоскости (β1) проведем (в произвольной точке) линию, перпендикулярную этому горизонтальному следу. Эта линия будет осью новой плоскости проекций π4, обозначим ее Х1,4. Теперь опустим перпендикуляры из точек А1, В1, С1 и S1 на ось Х1,4. Получим точки В4, А4, С4 и О4. Это точки основания пирамиды в новой плоскости проекций. У пирамиды есть вершина – S, которую мы еще не построили. Это можно сделать следующим образом: от точки О4 продолжим перпендикуляр вниз и на нем отложим отрезок h, равный расстоянию от S2O2 на фронтальной плоскости проекций.

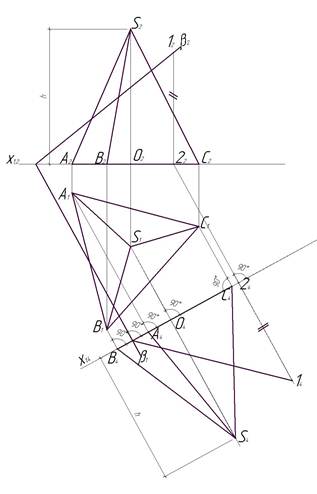
Рис. 15. Этап 1

Соединив точки А4, В4, С4 и S4, получим проекцию пирамиды во введенной плоскости П4. Теперь нужно построить в этой плоскости след секущей плоскости. Для этого на фронтальном следе β2 в любом месте ставим точку и обозначаем ее 12. Опускаем перпендикуляр из точки 12 на ось Х1,2 и получаем точку 22. Из точки 22 параллельно горизонтальному следу β1 проводим прямую до пересечения с осью Х1,4. Точку пересечения обозначим 24. Продолжим прямую 2224 за границу точки 24 на произвольную величину. На этой прямой отложим расстояние 2414, равное отрезку 1222, взятого с фронтальной плоскости проекций. Точку 14 соединим с точкой пересечения горизонтального следа β1 и осью плоскости проекций Х1,4.

Этим построением мы перевели секущую плоскость β в проецирующее положение, которое дает нам новые возможности в последующем построении сечения.

Рис. 16. Этап 2

Этап 2 (рис.16). Проецирующее положение секущей плоскости β4 дало нам возможность определить точки пересечения секущей плоскости и пирамиды. Это точки К4 и М4. Перенесем их проекции на горизонтальную плоскость проекций, используя проекционные связи (эти линии параллельны горизонтальному следу секущей плоскости – β1). На ребре S1C1 найдем точку К1, а на ребре А1S1 – точку М1. Еще две точки сечения (N2 и D2) мы найдем на горизонтальном следе секущей плоскости β1. Это точки ее пересечения с основанием пирамиды (со сторонами А1В1 и В1С1).

Соединив точки N1, M1, K1и D1, мы получим искомое сечение на горизонтальной плоскости проекций.

Найдем теперь точки этого сечения на фронтальной плоскости проекций. Для этого, опять используя проекционные связи, перенесем полученные точки на соответствующие им ребра во фронтальной проекции. Обозначим точки N2, M2, K2, D2 и соединим их отрезками.

Для определения видимости фигур нужно представить их в пространстве и, используя логику, можно прийти к выводу, что верхняя часть пирамиды закрывает секущую плоскость, мы ее не видим, по той же причине нам не видна сторона сечения М2К2.

Задача 2

На завершающем этапе задания необходимо построить натуральную величину найденного сечения. Для этого снова введем новую плоскость проекций.

Этап 3 ( рис.17). Для того, чтобы ввести новую плоскость проекций, параллельно следу β4 на произвольном расстоянии от него, проведем прямую линию – это будет ось новой плоскости проекций, обозначим ее Х4,5. Из точек М4, К4, N4 и D4 (точки N4 и D4 мы перенесли с горизонтальной проекции на ось Х1,4 и они совпали в одной точке) опустили перпендикуляры на ось Х4,5 и продолжили их на произвольную длину. На этих перпендикулярах (от оси Х4,5) отложили отрезки, равные расстояниям от оси Х1,4 до соответствующим им проекциям точек на горизонтальной плоскости проекций. Например, расстояние a – это расстояние от оси Х1,4 до точки К1, расстояние b – от оси Х1,4 до точки D1, расстояние c – от оси Х1,4 до точки N1, расстояние d – от оси Х1,4 до точки М1.

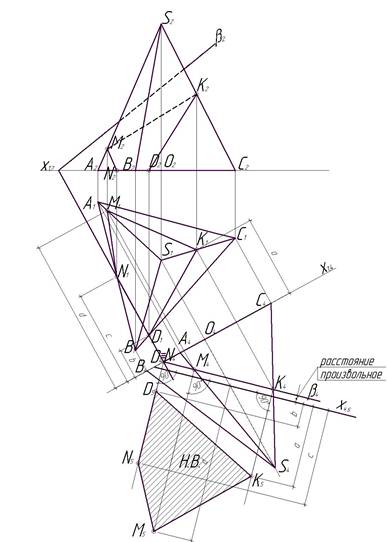
Рис. 17. Этап 3

Так как точки N4 и D4 по построению совпали, то они расположились на одной прямой. Обозначим полученные точки N5, M5, K5, D5. Соединив их отрезками, мы получим натуральную величину сечения пирамиды, плоскостью β, которая задана следами.

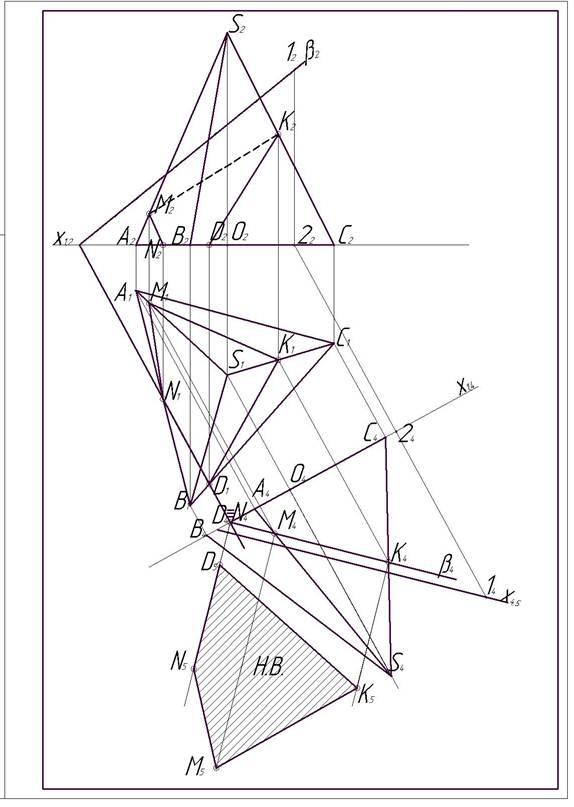
Рис. 18. Пример выполнения эпюра №2 (пример 2)