
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Пояснения к выполнению эпюра 2. (нахождение истинной величины сечения способом замены плоскостей проекций)
|
|
(нахождение истинной величины сечения способом замены плоскостей проекций)
Задача 1
В первой задаче контрольной работы требуется построить линию пересечения пирамиды с плоскостью и определить видимость пирамиды относительно секущей плоскости, а также секущей плоскости относительно пирамиды.
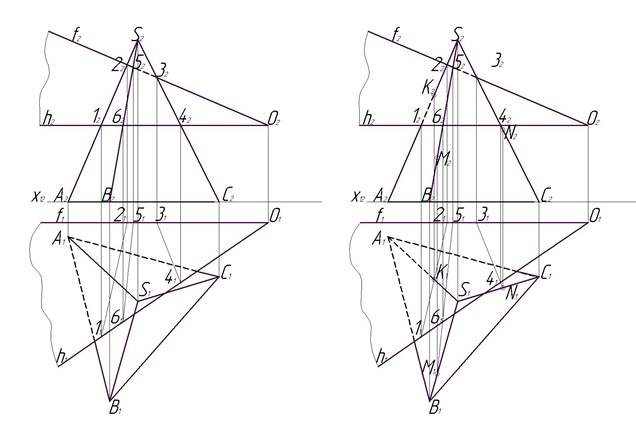
Рис. 10. Этап 1 Рис. 11. Этап 2
Этап 1 (рис.10). В данной задаче дана пирамида SАВС и секущая плоскость, представленная двумя пересекающимися в точке О прямыми, одна из которых, по заданию, является фронталью (f), а другая горизонталью (h).
Для построения линии пересечения, необходимо сначала найти точки пересечения ребер пирамиды секущей плоскостью. Построение начнем с фронтальной плоскости проекций. Определим точку пересечения горизонтали h2 c ребром S2А2 – это точка 12. Найдем горизонтальную проекцию точки 12 на горизонтальной проекции горизонтали – это точка 11. Теперь найдем точку пересечения фронтальной проекции фронтали f2 c ребром S2А2 и ее проекцию на горизонтальной плоскости проекций – это будут точки 22 и 21.
Аналогичным способом находим точки 32 и 42, рассматривая при этом пересечение прямых f2 и h2 c ребром S2C2 на фронтальной плоскости проекций и затем находя проекции точек на горизонтальной плоскости проекций – 31 и 41.
Точно также определяем точки пересечения прямых f2 и h2 с ребром S2B2 – это точки 52 и 62, а затем находим их соответствующие проекции на горизонтальной плоскости проекций – это точки 51 и 61. На горизонтальной плоскости проекций соединяем прямыми отрезками точки 11 и 21; 31 и 41; 51 и 61.
Этап 2 (рис.11). Следующий этап построения заключается в нахождении точек пересечения построенных отрезков с ребрами пирамиды на горизонтальной плоскости проекций. Рассмотрим отрезок 1121. Он пересекает ребро S1А1 в точке К1. Находим фронтальную проекцию точки К1 на фронтальной плоскости проекций на ребре S2А2, используя проекционную связь – это будет точка К2.
Для того, чтобы построить точку пересечения отрезка 3141 с ребром S1С1, необходимо продолжить отрезок 3141 за пределы точки 41. Точку пересечения обозначим N1. Найдем соответствующую проекцию этой точки на фронтальной плоскости проекций на ребре S2С2 и обозначим ее N2.
Аналогично поступим и с отрезком 5161. Продолжим его за пределы точки 61 и обозначим точку пересечения этой прямой с ребром S1В1. Это точка М1. Построим ее фронтальную проекцию на ребре S2В2 – это будет точка М2.
Таким образом, мы получили точки пересечения ребер пирамиды с секущей плоскостью.
Этап 3 (рис.12). На рисунке 12 показан дальнейший ход решения задачи. Для удобства его объяснения мы убрали линии предыдущих построений, оставив только точки пересечения ребер пирамиды с секущей плоскостью, но студентам этого делать не нужно – следует выполнять последующие построения, не убирая предыдущих.
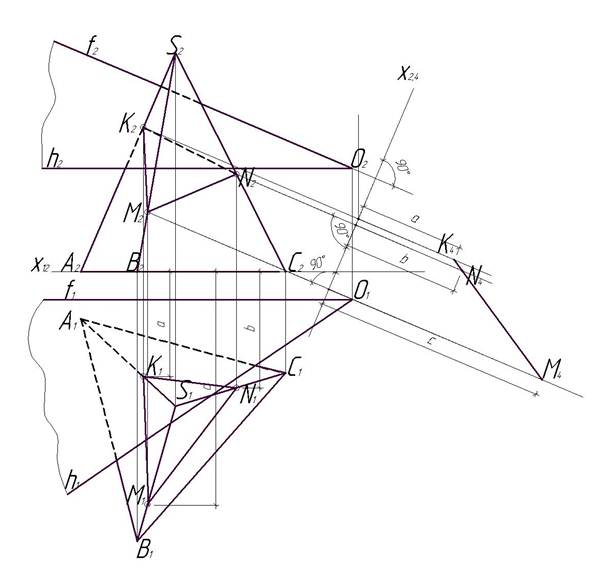
Рис. 12. Этап 3
Соединим точки К1, М1 и N1 на горизонтальной плоскости проекций, а также точки К2, М2 и N2 на фронтальной плоскости проекций.
Теперь мы будем делать построения на фронтальной плоскости проекций. Продолжим f2О2 на произвольную длину за пределы О2 и проведем к f2О2 перпендикулярную прямую. Этим действием мы задали новую плоскость проекций π4, перпендикулярную к фронтальной плоскости проекций π2. Обозначим ее ось - Х2,4.
Из точек К2, М2 и N2 проведем линии, перпендикулярные оси Х2,4 (пока произвольной длины).
На линии, проведенной из точки К2, начиная от оси Х2,4, отложим отрезок a, равный расстоянию от оси Х1,2 до К1 (на горизонтальной плоскости проекций). Полученную точку обозначим К4.
На линии, проведенной из точки N2, начиная от оси Х2,4, отложим отрезок b, равный расстоянию от оси Х1,2 до N1 (на горизонтальной плоскости проекций). Полученную точку обозначим N4.
На линии, проведенной из точки М2, начиная от оси Х2,4, отложим отрезок с, равный расстоянию от оси Х1,2 до М1 (на горизонтальной плоскости проекций). Полученную точку обозначим М4.
Точки К4, N4 и М4 соединим. Если построение сделано правильно, то должна получиться прямая линия.
Если кратко раскрыть смысл выполненных построений, то он заключается в том, что мы ввели новую плоскость проекций для того, чтобы сечение, представленное треугольником К2М2N2, заняло проецирующее положение относительно новой плоскости π4 и спроецировалось в прямую линию.
При определении видимости фигур нужно мысленно представить пирамиду и секущую плоскость в пространстве и, сопоставляя горизонтальную и фронтальную проекции, определить, какая часть пирамиды закрыта плоскостью, а какая часть плоскости закрыта пирамидой.
Задача 2
Этап 4 (рис.13). Мы подошли к последнему этапу выполнения эпюра 2. В этой задаче нужно построить истинную величину сечения. Для этого нам снова нужно ввести новую плоскость проекций, пусть это будет плоскость П 5. Параллельно построенной прямой К4N4М4 проведем прямую на любом расстоянии. Это будет ось Х4,5. Из точек К4, N4 и М4 проведем перпендикуляры на эту ось и продолжим их на произвольную длину.
На перпендикуляре, проведенном из точки К4, от оси Х4,5 отложим отрезок l1, равный расстоянию от оси Х2,4 до точки К2. Обозначим точку К5.
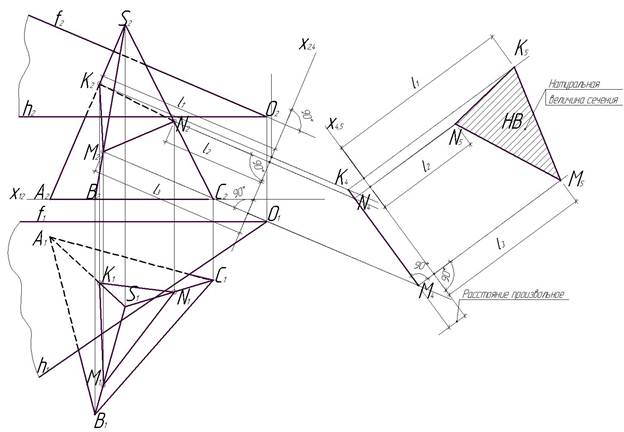 Рис. 13. Этап 4
Рис. 13. Этап 4
На перпендикуляре, проведенном из точки N4, от оси Х4,5 отложим отрезок l2, равный расстоянию от оси Х2,4 до точки N2. Обозначим точку N5.
На перпендикуляре, проведенном из точки M4, от оси Х4,5 отложим отрезок l3, равный расстоянию от оси Х2,4 до точки М2. Обозначим точку М5. Соединим полученные точки К5, N5 и М5.
Δ К5N5М5 – является натуральной величиной сечения пирамиды SАВС, полученного при пересечении ее секущей плоскостью, представленной двумя пересекающимися в точке О прямыми, одна из которых является фронталью (f), а другая горизонталью (h).
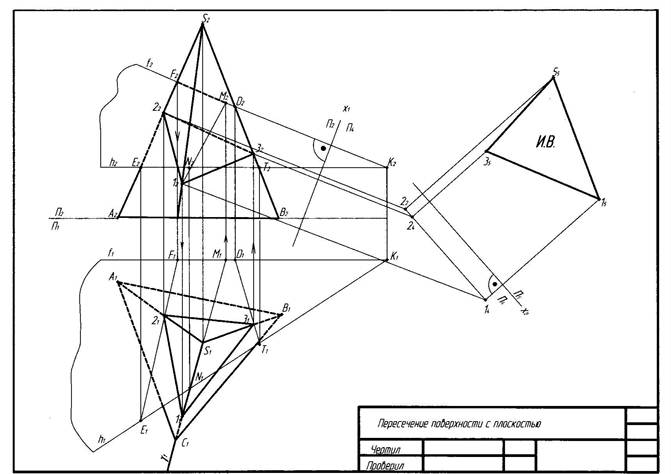
Рис. 14. Пример выполнения эпюра №2
Date: 2015-04-23; view: 1810; Нарушение авторских прав