Главная Случайная страница


Полезное:

Как сделать разговор полезным и приятным Как сделать объемную звезду своими руками Как сделать то, что делать не хочется? Как сделать погремушку Как сделать так чтобы женщины сами знакомились с вами Как сделать идею коммерческой Как сделать хорошую растяжку ног? Как сделать наш разум здоровым? Как сделать, чтобы люди обманывали меньше Вопрос 4. Как сделать так, чтобы вас уважали и ценили? Как сделать лучше себе и другим людям Как сделать свидание интересным?


Категории:

АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника






Пример разработки математической модели методом ПФЭ по результатам экспериментального обследования объекта химической технологии

⇐ ПредыдущаяСтр 7 из 7

Исследовался предел прочности при сжатии образцов цементов фосфатного твердения, выбранный выходным параметром (s, МН/м2).

Факторами являлись: Z 1 – температура термообработки, °С; Z 2 – время термообработки, ч; Z 3 – количество связки, %.

Необходимо получить математическое описание процесса по ПФЭ вида

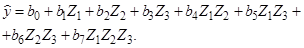
и оценить адекватность полученной модели.

Исходные данные: Z 10=500; Z 20=3; Z 30=25; D Z 1=200; D Z 2=2; D Z 3=8.

Матрица планирования:

№ оп X 0 Х 1 Х 2 Х 3 Х 1 Х 2 Х1Х3 Х 2 Х 3 Х 1 Х 2 Х 3 Y 1 Y 2
  +1 –1 +1 +1 –1 –1 +1 –1 79.30 75.35
  +1 +1 +1 +1 +1 +1 +1 +1 85.10 83.35
  +1 +1 –1 +1 –1 +1 –1 –1 59.40 60.33
  +1 +1 +1 –1 +1 –1 –1 –1 72.50 77.79
  +1 –1 –1 +1 +1 –1 –1 +1 42.30 45.70
  +1 –1 –1 –1 +1 +1 +1 –1 48.70 42.56
  +1 –1 +1 –1 –1 +1 –1 +1 62.50 63.46
  +1 +1 –1 –1 –1 –1 +1 +1 51.40 59.79

1. Расчет средних значений по формуле (11),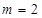

 

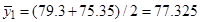
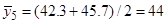
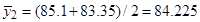
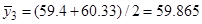
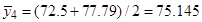
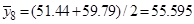
2. Определение построчной дисперсии по формуле (12):

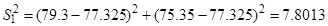
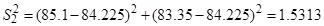
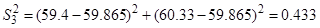
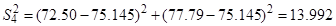
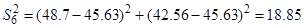
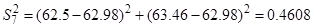
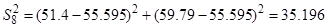
3. Проверка однородности построчных дисперсий по критерию Кохрена – формула (13):

, ,

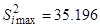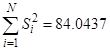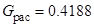
Полученное значение сравнивается с табличным 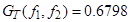, . Так как 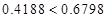, дисперсии однородны.

4. Определение ошибки опыта или дисперсии воспроизводимости – (14):

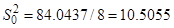
5. Вычисление коэффициентов уравнения регрессии – (15):

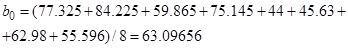
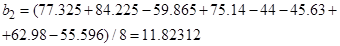
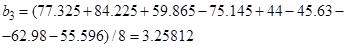
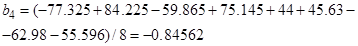
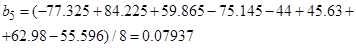
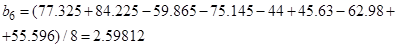
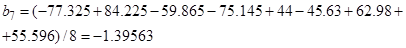6. Вычисление дисперсии коэффициентов уравнения регрессии и расчетных значений критерия Стьюдента, (16)–(17)

;

;

;

;

;

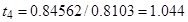
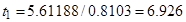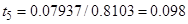
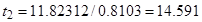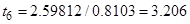
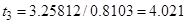7. Проверка значимости коэффициентов уравнения регрессии:

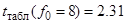
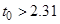
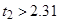
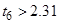
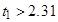
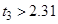
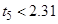
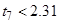
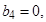
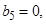
Следовательно, принимаем 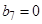, так как они незначимы.

6. Полученное уравнение регрессии имеет вид:

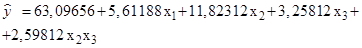
Определим расчетные значения выходного параметра для каждого опыта по уравнению регрессии:

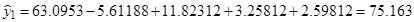
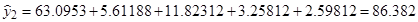
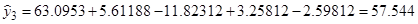
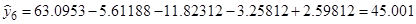
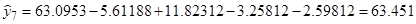
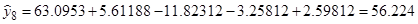
7. Расчет дисперсии адекватности по формуле (18):

8. Определение расчетного значения критерия Фишера – (19):

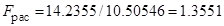
9. Проверка адекватности полученного уравнения по критерию Фишера: 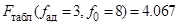, 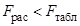. Следовательно, полученная модель адекватно описывает процесс сжатия образцов цементов фосфатного твердения.

 

10. Раскодировка уравнения регрессии

В результате обработки результатов ПФЭ получено уравнение регрессии:

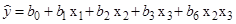
Факторы 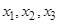входят в него в кодированном виде. Чтобы получить уравнение в натуральном масштабе, необходимо воспользоваться формулами (4):

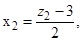
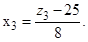
После подстановки получим

 

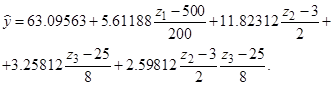
Окончательно уравнение регрессии в реальном масштабе имеет следующий вид:

.


 

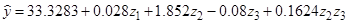Проверка адекватности полученного уравнения по критерию Фишера: ,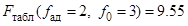

 

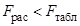
2. Индивидуальные задания на курсовую работу по курсу
«Математическое моделирование и применение ЭВМ в химической технологии»

Задание № 1.

При разработке цементов фосфатного твердения исследуется предел прочности при сжатии образцов, принятый в качестве выходного параметра (s, МН/м2).

Факторами являлись:

Z 1 – температура термообработки, °С;

Z 2 – время термообработки, ч;

Z 3 – количество связки, %.

Необходимо получить математическое описание процесса по ПФЭ вида

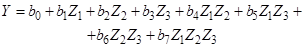
и оценить адекватность полученной модели.

Исходные данные: Z 10=500; Z 20=3; Z 30=25; D Z 1=200; D Z 2=2; D Z 3=8.

 

Матрица планирования:

№ оп. X 0 Х 1 Х 2 Х 3 Х 1 Х 2 Х 1 Х 3 Х 2 Х 3 Х 1 Х 2 Х 3 Y 1 Y 2
  +1 +1 +1 +1           83.4
  +1 –1 +1 +1         79.4 75.2
  +1 +1 –1 +1         59.3 60.2
  +1 –1 –1 +1         42.2 41.8
  +1 +1 +1 –1         72.4 77.8
  +1 –1 +1 –1         62.3 61.4
  +1 +1 –1 –1         51.3 54.8
  +1 –1 –1 –1         48.8 42.4

Задание № 2.

При разработке корундовых изделий исследуется истинная пористость образцов, принятая в качестве выходного параметра (Y, %).

Факторами являлись:

Z 1 – температура спекания, °С;

Z 2 – количество спекающей добавки Ti O2, %;

Z 3 – время обжига, ч.

Необходимо получить математическое описание процесса по ПФЭ вида


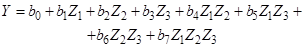
и оценить адекватность полученной модели.

Исходные данные: Z 10=1600; Z 20=1; Z 30=4; D Z 1=100; D Z 2=0.5; D Z 3=2.

 

Матрица планирования:

№ оп. Х 0 Х 1 Х 2 Х 3 Х 1 Х 2 Х 1 Х 3 Х 2 Х 3 Х 1 Х 2 Х 3 Y 1 Y 2
  +1 –1 –1 –1         3.75 3.68
  +1 –1 +1 +1         2.75 2.79
  +1 –1 +1 –1         0.5 0.53
  +1 –1 –1 +1         2.25 2.28
  +1 +1 –1 –1         2.75 2.72
  +1 +1 –1 +1         0.75 0.7
  +1 +1 +1 –1         1.0 0.96
  +1 +1 +1 +1         0.5 0.48

Задание № 3.

При разработке жаростойких покрытий титановых сплавов на основе фосфатных связующих оценивается их термостойкость, определяемая числом теплосмен в режиме 700°С – вода до появления признаков разрушения, принятая в качестве выходного параметра (Y).

Факторами являлись:

Z 1 – рН связки;

Z 2 – количество связки, %;

Z 3 – соотношение компонентов в наполнителе.

Необходимо получить математическое описание процесса по ПФЭ вида

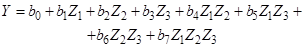
и оценить адекватность полученной модели.

Исходные данные: Z 10=2; Z 20=30; Z 30=1:1; D Z 1=1; D Z 2=10; D Z 3=1:5.

 

Матрица планирования:

№ оп. Х 0 Х 1 Х 2 Х 3 Х 1 Х 2 Х 1 Х 3 Х 2 Х 3 Х 1 Х 2 Х 3 Y 1 Y 2
  +1 +1 +1 +1            
  +1 +1 +1 –1            
  +1 +1 –1 +1            
  +1 +1 –1 –1            
  +1 –1 –1 +1            
  +1 –1 +1 –1            
  +1 –1 +1 +1            
  +1 –1 –1 –1            

Задание № 4.

При изучении кинетики измельчения глинозема исследуется намол железа в стальных мельницах стальными шарами, принимаемый в качестве выходного параметра (Y, %).

Факторами являлись:

Z 1 – время измельчения, ч;

Z 2 – диаметр мелющих тел, мм;

Z 3 – соотношение глинозем – шары.

Необходимо получить математическое описание процесса по ПФЭ вида

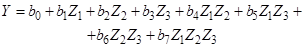
и оценить адекватность полученной модели.

Исходные данные: Z 10=25; Z 20=15; Z 30=1:2; D Z 1=5; D Z 2=5; D Z 3=1:3.

 

Матрица планирования:

№ оп. Х 0 Х 1 Х 2 Х 3 Х 1 Х 2 Х 1 Х 3 Х 2 Х 3 Х 1 Х 2 Х 3 Y 1 Y 2
  +1 –1 –1 –1           3.1
  +1 +1 –1 –1         2.7 2.9
  +1 –1 +1 –1         2.6 2.2
  +1 +1 +1 –1         2.2 2.0
  +1 –1 –1 +1         3.8 4.1
  +1 +1 –1 +1         3.64 3.9
  +1 –1 +1 +1         3.4 3.7
  +1 +1 +1 +1         3.09 3.22

Задание № 5


При синтезе керметов системы W–Al2O3 исследуется предел прочности при сжатии образцов, принимаемый в качестве выходного параметра (s, МН/м2).

Факторами являлись:

Z 1 – соотношение W:Al2O3;

Z 2 – количество спекающей добавки Z r, %;

Z 3 – температура спекания в вакууме, °С.

Необходимо получить математическое описание процесса по ПФЭ вида

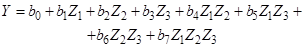
и оценить адекватность полученной модели.

Исходные данные: Z 10=1:2; Z 20=5; Z 30=1800; D Z 1=1:4; D Z 2=2; D Z 3=100.

 

Матрица планирования:

№ оп. Х 0 Х 1 Х 2 Х 3 Х 1 Х 2 Х 1 Х 3 Х 2 Х 3 Х 1 Х 2 Х 3 Y 1 Y 2
  +1 –1 –1 –1            
  +1 +1 –1 –1            
  +1 –1 +1 –1            
  +1 +1 +1 –1            
  +1 –1 –1 +1            
  +1 +1 –1 +1            
  +1 –1 +1 +1            
  +1 +1 +1 +1            

Задание № 6.

Исследуемый процесс – экстракция в системе растительный материал – жидкость, в качестве выходного параметра рассматривается степень извлечения твердой фазы (Y,%).

Факторами являлись:

Z 1 – соотношение фаз, т/ж;

Z 2 – число оборотов мешалки, об/мин;

Z 3 – диаметр частиц, см.

Необходимо получить математическое описание процесса по ПФЭ вида

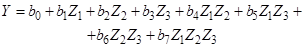
и оценить адекватность полученной модели.

Исходные данные: Z 10=0.015; Z 20=550; Z 30=0.0505; D Z 1=0.005; D Z 2=450; D Z 3=0.0495.

 

Матрица планирования:

№ оп. Х 0 Х 1 Х 2 Х 3 Х 1 Х 2 Х 1 Х 3 Х 2 Х 3 Х 1 Х 2 Х 3 Y 1 Y 2
  +1 +1 +1 +1         80.2 77.6
  +1 +1 –1 +1         76.2 77.6
  +1 –1 +1 +1         86.8 89.4
  +1 –1 –1 +1         81.0 81.3
  +1 +1 +1 –1         87.6 87.4
  +1 +1 –1 –1         89.7 91.6
  +1 –1 +1 –1         91.3 91.6
  +1 –1 –1 –1         94.3 93.8

 



Задание № 7.

Исследуется процесс гидратации диизопропилового эфира с целью получения изопропилового спирта. В качестве выходного параметра выбирается выход изопропилового спирта (Y, %).

Факторами являлись:

Z 1 – температура процесса, °С;

Z 2 – расход диизопропилового эфира, л/мин;

Z 3 – концентрация диизопропилового эфира, %.

Необходимо получить математическое описание процесса по ПФЭ (особый случай) вида

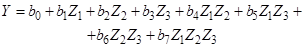
и оценить адекватность полученной модели.

Исходные данные: Z 10=250; Z 20=0.3; Z 30=0.5; D Z 1=15; D Z 2=0.05; D Z 3=0.1.

 

Матрица планирования:

№ оп. Х 0 Х 1 Х 2 Х 3 Х 1 Х 2 Х 1 Х 3 Х 2 Х 3 Х 1 Х 2 Х 3 Y
  +1 –1 –1 –1         72.2
  +1 +1 –1 –1         71.3
  +1 –1 +1 –1         49.1
  +1 +1 +1 –1         70.46
  +1 –1 –1 +1         19.63
  +1 +1 –1 +1         32.58
  +1 –1 +1 +1         57.55
  +1 +1 +1 +1         46.02
  +1               85.9
  +1                
  +1               87.9

Задание № 8.

Исследуется процесс отравления катализатора сернистыми соединениями. В качестве выходного параметра принимается критерий стабильности катализатора.

Факторами являлись:

Z 1 – концентрация палладия, %;

Z 2 – концентрация селена, %;

Z 3 – концентрация серы, %.

Необходимо получить математическое описание процесса по ПФЭ (особый случай) вида

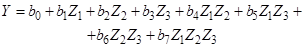
и оценить адекватность полученной модели.

Исходные данные: Z 10=0.55; Z 20=1.0; Z 30=0.033; D Z 1=0.45; D Z 2=0.5; D Z 3=0.027.

 

Матрица планирования:

№ оп. Х 0 Х 1 Х 2 Х 3 Х 1 Х 2 Х 1 Х 3 Х 2 Х 3 Х 1 Х 2 Х 3 Y
  +1 +1 –1 +1         1.43
  +1 –1 –1 +1         2.42
  +1 +1 +1 +1         1.33
  +1 –1 +1 +1         2.86
  +1 +1 –1 –1         1.40
  +1 –1 –1 –1         6.67
  +1 +1 +1 –1         1.56
  +1 –1 +1 –1         4.40
  +1 +1 +1 +1         1.34
  +1 +1 +1 +1         1.32
  +1 +1 +1 +1         1.35

Задание № 9.

Исследуется изотермический процесс кристаллизации фторида алюминия из водных растворов в промышленных условиях его получения. В качестве выходного параметра выбирается средняя скорость кристаллизации за время опыта.

Факторами являлись:

Z 1 – температура раствора, °С;

Z 2 – концентрация раствора, %;

Z 3 – время, ч.

Необходимо получить математическое описание процесса по ПФЭ (особый случай) вида

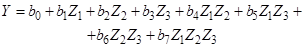
и оценить адекватность полученной модели.

Исходные данные: Z 10=90; Z 20=22; Z 30=2; D Z 1=10; D Z 2=4; D Z 3=0.5.

 

Матрица планирования:

№ оп. Х 0 Х 1 Х 2 Х 3 Х 1 Х 2 Х 1 Х 3 Х 2 Х 3 Х 1 Х 2 Х 3 Y
  +1 +1 +1 +1         9.86
  +1 –1 +1 +1         9.09
  +1 +1 –1 +1         6.35
  +1 –1 –1 +1         6.41
  +1 +1 +1 –1         15.0
  +1 –1 +1 –1         12.02
  +1 +1 –1 –1         15.48
  +1 –1 –1 –1         9.52
  +1               9.12
  +1               10.3
  +1               10.25

Задание № 10.

Исследуется процесс восстановления сульфата натрия газовой смесью. состоящей из 25% СО и 75% Н. В качестве выходного параметра выбираются затраты.

Факторами являлись:

Z 1 – температура опыта, °К;

Z 2 – скорость газа, м/с;

Z 3 – время, с.

Необходимо получить математическое описание процесса по ПФЭ (особый случай) вида

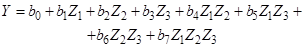
и оценить адекватность полученной модели.

Исходные данные: Z 10=1373; Z 20=0.274; Z 30=480; D Z 1=100; D Z 2=0.106; D Z 3=120.

 

Матрица планирования:

№ оп. Х 0 Х 1 Х 2 Х 3 Х 1 Х 2 Х 1 Х 3 Х 2 Х 3 Х 1 Х 2 Х 3 Y
  +1 –1 –1 –1         115.89
  +1 –1 –1 +1         76.18
  +1 –1 +1 –1         78.77
  +1 –1 +1 +1         84.1
  +1 +1 –1 –1         79.08
  +1 +1 –1 +1         70.2
  +1 +1 +1 –1         70.32
  +1 +1 +1 +1         82.08
  +1               79.925
  +1               75.62
  +1               78.45
  +1               75.66

Задание № 11.

Исследуется процесс восстановления сульфата натрия газовой смесью, состоящей из 25% СО и 75% Н. В качестве выходного параметра выбирается выход целевого продукта.

Факторами являлись:

Z 1 – температура опыта, °К;

Z 2 – скорость газа, м/с;

Z 3 – время, с.

Необходимо получить математическое описание процесса по ПФЭ (особый случай) вида

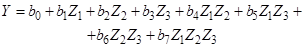
и оценить адекватность полученной модели.

Исходные данные: Z 10=1373; Z 20=0.274; Z 30=480; D Z 1=100; D Z 2=0.106; D Z 3=120.

 

Матрица планирования:

№ оп. Х 0 Х 1 Х 2 Х 3 Х 1 Х 2 Х 1 Х 3 Х 2 Х 3 Х 1 Х 2 Х 3 Y
  +1 –1 –1 –1         49.6
  +1 –1 –1 +1         81.0
  +1 –1 +1 –1         80.5
  +1 –1 +1 +1         85.0
  +1 +1 –1 –1         73.0
  +1 +1 –1 +1         88.0
  +1 +1 +1 –1         90.0
  +1 +1 +1 +1         83.0
  +1               79.5
  +1               84.0
  +1               81.0
  +1               84.0

Задание № 12.

Исследуется процесс разделения эмульсии в гравитационном отстойнике с насадкой. Выходным параметром Y является время разделения эмульсии в отстойнике.

Факторами являлись:

Z 1 – диаметр капель эмульсии, м;

Z 2 – линейная скорость движения эмульсии в отстойнике, м/с;

Z 3 – соотношение фаз на входе в отстойник.

Необходимо получить математическое описание процесса по ПФЭ вида

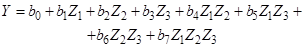
и оценить адекватность полученной модели.

Исходные данные: Z 10=0.75×10–3; Z 20=14.025×10–3; Z 30=1:1; D Z 1=0.25×10–3; D Z 2=1.775×10–3; D Z 3=0.9.

 

Матрица планирования:

№ оп. Х 0 Х 1 Х 2 Х 3 Х 1 Х 2 Х 1 Х 3 Х 2 Х 3 Х 1 Х 2 Х 3 Y 1 Y 2
  +1 +1 +1 +1         5.36 5.65
  +1 +1 –1 +1         6.4 6.69
  +1 –1 +1 +1         10.1 10.456
  +1 –1 –1 +1         12.95 13.37
  +1 +1 +1 –1           4.2
  +1 +1 –1 –1         4.9 5.35
  +1 –1 +1 –1         6.52 6.82
  +1 –1 –1 –1         8.026 8.471

Задание № 13.

Исследуется процесс хлорирования 4–этил–5(b–оксиэтил)–тиазола. Выходным параметром Y является выход 4–метил–5(b–оксиэтил)–тиазола из гемитиамина. Каждый опыт проводился трижды, что позволило определить ошибку опыта 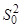=6.19.

Факторами являлись:

Z 1 – продолжительность выдержки при кипении, ч;

Z 2 – избыток хлористого тианила против стехиометрического количества, %;

Z 3 – температура реакций, °С.

Необходимо получить математическое описание процесса по ПФЭ вида

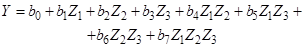
и оценить адекватность полученной модели.

Исходные данные: Z 10=2; Z 20=2; Z 30=5; D Z 1=1; D Z 2=0.5; D Z 3=5.

 

Матрица планирования:

№ оп. Х 0 Х 1 Х 2 Х 3 Х 1 Х 2 Х 1 Х 3 Х 2 Х 3 Х 1 Х 2 Х 3 Y ср
  +1 +1 +1 +1         67.91
  +1 –1 +1 +1         65.67
  +1 +1 –1 +1         63.16
  +1 –1 –1 +1         67.14
  +1 +1 +1 –1         83.04
  +1 –1 +1 –1         74.23
  +1 +1 –1 –1         71.37
  +1 –1 –1 –1         65.25

 


Задание № 14.

Исследуется процесс ацилирования анилина хлорангидридом 9–флуоренон–4 карбоновой кислоты. Выходным параметром Y (%) является выход при анализе хлорангидрида 9–флуоренон–4 карбоновой кислоты.

Факторами являлись:

Z 1 – температура реакции, °С;

Z 2 – продолжительность реакции, мин;

Z 3 – количество растворителя, г.

Необходимо получить математическое описание процесса по ПФЭ вида

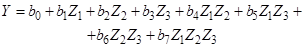
и оценить адекватность полученной модели.

Исходные данные: Z 10=120; Z 20=75; Z 30=20; D Z 1=10; D Z 2=45; D Z 3=10.

 

Матрица планирования:

№ оп. Х 0 Х 1 Х 2 Х 3 Х 1 Х 2 Х 1 Х 3 Х 2 Х 3 Х 1 Х 2 Х 3 Y 1 Y 2
  +1 –1 –1 –1         79.5  
  +1 +1 –1 –1         84.8 84.4
  +1 –1 +1 –1         85.4 85.6
  +1 –1 –1 +1         83.1 82.1
  +1 +1 +1 –1         90.3 88.9
  +1 +1 –1 +1         83.5 84.4
  +1 –1 +1 +1         85.2 85.6
  +1 +1 +1 +1         88.3 89.5

Задание № 15.

Исследуется процесс выделения ртути из отработанного электролита. Выходным параметром Y (%) является степень очистки раствора от ртути.

Факторами являлись:

Z 1 – время контакта, мин;

Z 2 – количество ионообменной смолы, загруженной в аппарат, г;

Z 3 – расход аналита, л/с.

Необходимо получить математическое описание процесса по ПФЭ вида

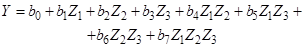
и оценить адекватность полученной модели.

Исходные данные: Z 10=5; Z 20=11; Z 30=1.25; D Z 1=0.5; D Z 2=1.5; D Z 3=0.25.

 

Матрица планирования:

№ оп. Х 0 Х 1 Х 2 Х 3 Х 1 Х 2 Х 1 Х 3 Х 2 Х 3 Х 1 Х 2 Х 3 Y 1 Y 2
  +1 +1 +1 +1         93.18 92.62
  +1 –1 +1 +1         94.43 96.4
  +1 +1 –1 +1         80.99 77.61
  +1 –1 –1 +1         84.20 82.8
  +1 +1 +1 –1         96.65 94.95
  +1 –1 +1 –1         99.07 97.93
  +1 +1 –1 –1         89.25 92.75
  +1 –1 –1 –1         92.91 90.09

 

 


Задание № 18

При синтезе изделий из окиси магния изучается усадка образцов Y,%, принимаемая в качестве выходного параметра.

Факторами являлись:

Z 1 – температура спекания, °С;

Z 2 – давление прессования, Н/м2;

Z 3 – выдержка при температуре обжига, ч;

Z 4 – количество спекающей добавки, %.

Необходимо получить математическое описание процесса вида

,

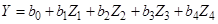используя полуреплику от ПФЭ 24 с определяющим контрастом 1= Х 1 Х 2 Х 3 Х 4 и оценить адекватность полученной модели. Определить систему смешанных оценок.

Исходные данные: Z 10=1600; Z 20=300; Z 30=4; Z 40=2; D Z 1=80; D Z 2=100; D Z 3=2; D Z 4=2.

 

Матрица планирования:

№ оп. Х 0 Х 1 Х 2 Х 3 Х 4 Y 1 Y 2
  +1 –1 –1 –1 –1 4.7 4.83
  +1 +1 –1 +1 –1 3.6 3.7
  +1 –1 –1 +1 +1   5.14
  +1 –1 +1 –1 +1 3.4 3.6

⇐ Предыдущая1234567





Date: 2015-05-22; view: 559; Нарушение авторских прав


mydocx.ru - 2015-2024 year. (0.123 sec.) Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав - Пожаловаться на публикацию