
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Дробный факторный эксперимент
|
|
Полный факторный эксперимент является весьма эффективным средством получения математической модели исследуемого объекта, особенно при числе факторов k>3. Однако увеличение числа факторов приводит к резкому увеличению числа опытов. Так, ПФЭ 26 требует постановки 64 опытов, а 27 – 128 опытов. Конечно, точность модели при увеличении числа опытов также возрастает, однако это приводит к большим затратам средств и времени.
Практика показывает, что для получения достаточно точных оценок коэффициентов регрессии можно обойтись малым количеством опытов, вводя понятие дробного факторного эксперимента или дробных реплик, который представляет собой некоторую часть (1/2, 1/4, 1/8 и т.д.) от полного факторного эксперимента.
Сокращение числа опытов влечет за собой появление корреляции между оценками коэффициентов. Это обстоятельство не позволяет раздельно оценивать эффекты факторов и эффекты взаимодействия. Получаются так называемые смешанные оценки.
Для дробных реплик используются специальные алгебраические соотношения, облегчающие выявление смешанных эффектов. Они называются генерирующими соотношениями и определяющими контрастами.
Генерирующим называется соотношение, которое показывает, какое из взаимодействий факторов принято незначимым по влиянию на выходную переменную, а поэтому может быть заменено в матрице планирования новой независимой переменной. Например, вместо плана 23 можно использовать его полу реплику – план 23–1. Если в качестве генерирующего соотношения выбрать
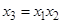 , (23)
, (23)
то для построения уравнения регрессии достаточно четырех опытов, а качестве плана можно использовать расширенную матрицу планирования для эксперимента 22 (табл. 3)
Таблица 3
| № оп. | X 0 | Х 1 | Х 2 | X 3= Х 1 Х 2 |
| +1 | –1 | –1 | +1 | |
| +1 | –1 | +1 | –1 | |
| +1 | +1 | –1 | –1 | |
| +1 | +1 | +1 | +1 |
С генерирующими соотношениями можно производить алгебраические операции: умножать левую и правую часть на любые эффекты – линейные и определенные взаимодействия. При этом если фактор входит в уравнение в квадрате или другой четной степени, то он заменяется единицей. Умножив обе части генерирующего соотношения (23) на 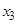 получим
получим 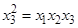 или
или
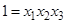 (24)
(24)
Это и есть определяющий контраст, соотношение, которое задает элементы первого столбца.
Зная определяющий контраст, можно получить систему смешанных оценок для данной дробной реплики. Для этого определяющий контраст умножается на каждый фактор и взаимодействие факторов. В рассматриваемом примере для полуреплики от плана 23 смешанные оценки коэффициентов уравнения регрессии задаются следующими соотношениями:
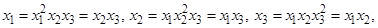 (25)
(25)
что соответствует оценкам
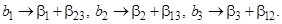 (26)
(26)
Эффективность системы смешивания факторов и взаимодействия факторов определяется так называемой разрешающей способностью матрицы. Она считается максимальной, если линейные эффекты смешаны с эффектами взаимодействия наиболее высоких порядков.
Для построения дробных реплик большей степени дробности (2 k–p, р – число вновь введенных в рассмотрение факторов) необходимо задать столько генерирующих соотношений либо определяющих контрастов, сколько эффектов взаимодействия заменяются новыми независимыми факторами. Например, в плане типа 25–2 могут быть заданы такие генерирующие соотношения:
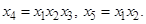 (27)
(27)
Определяющие контрасты для этой реплики будут таковы:
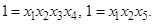 (28)
(28)
Перемножив определяющие контрасты между собой, получим так называемый обобщающий определяющий контраст, который с учетом (28) полностью характеризует разрешающую способность реплики высокой степени дробности:
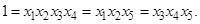 (29)
(29)
При этом получается следующая система смешанных оценок для линейных эффектов
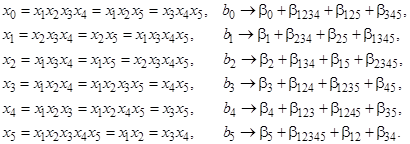
Обработка результатов ДФЭ осуществляется по тому же алгоритму, что и ПФЭ – соотношения (11) – (19).
Date: 2015-05-22; view: 759; Нарушение авторских прав