Алгоритм обработки результатов ПФЭ

1. В каждой строке матрицы планирования рассчитываются среднее значение по m параллельным опытам и построчная или выборочная дисперсия:

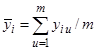, i = 1,2,..., N. (11)

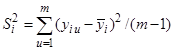, i = 1,2,..., N. (12)

2. Проверяется однородность выборочных дисперсий по критерию Кохрена:

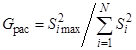, (13)

полученное значение сравнивается с табличным 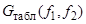. 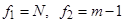– числа степеней свободы, по которым определяется табличное значение.[1] Если 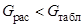, то дисперсии однородны. Это означает, что все опыты были проведены с одинаковой точностью и расчет может быть продолжен. Если гипотеза об однородности дисперсий не подтверждается, то одними из решений являются увеличение числа параллельных опытов, изменение метода контроля выходной переменной, масштабирование выходной переменной.

3. Определяется ошибка опыта или дисперсия воспроизводимости:

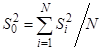. (14)

4. Коэффициенты уравнения регрессии определяются по формуле:

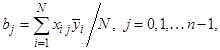(15)

где n – число столбцов матрицы планирования.

Для оценки значимости коэффициента b_j вычисляется его дисперсия – одинаковое значение для всех коэффициентов:

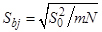(16)

и расчетное значение критерия Стьюдента:

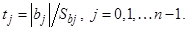(17)

Если 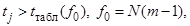то j –ый коэффициент считается значимым, если 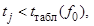то коэффициент принимается равным нулю, т.е. соответствующий фактор или взаимодействие факторов исключается из уравнения регрессии. Исключение незначимого коэффициента не скажется на других коэффициентах, при этом выборочные коэффициенты 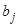оказываются так называемыми несмешанными оценками для соответствующих коэффициентов генеральной совокупности 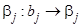, т.е. коэффициенты уравнения регрессии характеризуют вклад каждого фактора и взаимодействия факторов в выходную величину. Причины незначимости коэффициентов уравнения регрессии могут быть следующие: 1) фактор 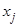включен в рассмотрение ошибочно и он не влияет на выходной параметр Y; 2) выбран слишком малый интервал варьирования .

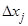5. После того, как уравнение регрессии получено в окончательном виде, проверяется его адекватность. Для этого рассчитывается дисперсия адекватности:

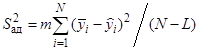. (18)

Здесь 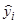– значение выходного параметра, рассчитанное по полученному уравнению регрессии, L – число значимых коэффициентов в уравнении регрессии. Затем рассчитывается значения критерия Фишера:

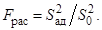(19)

Если 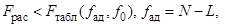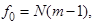то полученное уравнение адекватно описывает исследуемый процесс. При неадекватности модели наиболее часто принимают решение об уменьшении интервала варьирования факторов и повторении эксперимента. Такое решение, хотя и уменьшает кривизну поверхности отклика, однако, может привести к появлению незначимых коэффициентов. Очень эффективно включать в план эксперимента новый фактор из числа отсеянных при предварительных экспериментах.

Date: 2015-05-22; view: 796; Нарушение авторских прав