Лекция №1. По основам квантовой механики

С.Г. Сучков

ЛЕКЦИИ

По основам квантовой механики

Учебное пособие для студентов, обучающихся по специальностям:

010803 –Микроэлектроника и полупроводниковые приборы,

210104 – Микроэлектроника и твердотельная электроника,

210601 – Нанотехнология в электронике,

150601 – Материаловедение и технология новых материалов,

010707 – Медицинская физика;

и направлениям:

210600 – Нанотехнология (бак.),

210100 – Электроника и микроэлектроника (бак.),

210108 – Электроника и микроэлектроника (маг.),

010700 – Физика (маг. Физика полупроводников. Микроэлектроника).

Саратов

Лекция №1

Истоки квантовой теории

Понятие квант возникло в физике в 1900 г., оно было введено немецким физиком Максом Планком (от латинского слова «сколько») и означало минимальную порцию энергии, которую излучало абсолютно черное тело. Отказ от непрерывного изменения энергии позволил Планку вывести формулу, правильно описывающую спектр излучения абсолютно черного тела и, тем самым, устранить так называемую «ультрафиолетовую катастрофу» - неограниченное увеличение энергии излучения абсолютно черного тела в коротковолновой части спектра (длины волн короче оптических, отсюда происхождение термина «ультрафиолетовая»). Для вывода своей формулы Планку необходимо было ввести величину энергии, соответствующей кванту излучения в виде

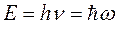, (1.1)

где n - частота излучения, h=2p ħ = 6.61·10^-22 (Дж·сек) - некоторая постоянная, определенная из условия совпадения экспериментальных и расчетных значений плотности равновесного излучения частоты ω и температуры Т, определяемых формулой Планка

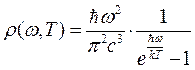(1.2)

В течение 5 лет научная общественность не проявляла никакого интереса к работе Планка, считая понятие кванта лишь математическим трюком. Но в 1905 г. двадцатишестилетний А.Эйнштейн, основываясь на гипотезе Планка, дал простое и полное объяснение фотоэлектрическому эффекту, открытому Столетовым в 1885г. и с тех пор бывшим загадкой для физиков. Из классических представлений о свете, как о непрерывном волновом процессе, следовало, что при увеличении интенсивности света, т.е. при увеличении амплитуды электрического поля волны, скорость вырываемых из металла электронов должна увеличиваться, но на опыте этого не происходило. Скорость электронов зависела только от длины волны излучения, но не от его амплитуды! Эйнштейн предположил, что, если свет представить в виде потока частиц, названных им фотонами, имеющих энергию, определяемую формулой (1.1), то переданная электронам энергия фотонов определяется только частотой излучения, но не его амплитудой. За объяснение фотоэффекта А.Эйнштейн в 1919 г. был удостоен Нобелевской премии, М.Планк получил Нобелевскую премию годом раньше за объяснение закона излучения абсолютно черного тела.

После открытия электрона в 1897 г. Дж.Дж.Томсоном была предложена модель атома, по которой он представлял собой шарик из положительно заряженной жидкости, в которой двигались по орбитам, образуя оболочки, электроны в количестве, необходимом для того, чтобы атом был нейтральным. Такая модель позволила на основе законов классической физики объяснить многие свойства веществ, например, термоэлектронную эмиссию, некоторые химические свойства и т.д. Но в 1911 г. Резерфорд на основе своих опытов по бомбардировке α-частицами атомов золота установил, что положительный заряд и почти вся масса атома сосредоточены в очень маленьком ядре, радиус которого в 10000 раз меньше радиуса атома, а электроны движутся вокруг ядра по орбитам подобно планетам вокруг Солнца. Планетарная модель атома соответствовала экспериментальным данным, но не допускала объяснения с точки зрения законов классической физики, в частности, электродинамики. Известно, что ускоренно движущийся заряд излучает электромагнитные волны, причем интенсивность излучения I пропорциональна квадрату ускорения а в соответствии с формулой:

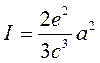
Поэтому в течение короткого промежутка времени (порядка микросекунды) электроны, вращающиеся вокруг ядра, должны были бы упасть на ядро и атом имел бы размеры своего ядра, что противоречит опытным данным по размеру атомов.

В 1913 году Нильс Бор на основе анализа линейчатого спектра водорода и формулы Бальмера построил квантовую модель атома, в которой точно рассчитывалась постоянная Ридберга и все спектральные линии водорода (красная, зеленая, фиолетовая и ультрафиолетовые). В основе этой модели лежали постулаты о том, что существует дискретный набор орбит, на которых электроны не излучают, а излучение происходит при переходе электрона с вышележащей орбиты на нижележащую. И хотя теория Бора не объясняла спектры атомов более тяжелых элементов, а, тем более, молекул, она показала окончательно, что в микромире действуют другие законы движения частиц, и открыла эпоху построения квантовой механики.

Основные представления квантовой механики

Луи Де Бройль в 1921 г., обобщив известные к тому времени экспериментальные данные по давлению света, по фотоэффекту и эффекту Комптона, демонстрировавшие корпускулярные (квантовые) свойства света, высказал гипотезу о единстве волновых и корпускулярных свойств материи (корпускулярно-волновой дуализм «волна-частица»). Он ввел представление о том, что любая материальная частица обладает волновыми свойствами, а любая волна может рассматриваться как поток материальных частиц. Так, с одной стороны, по Планку, энергия фотона Е=hn, с другой, по Эйнштейну, – его энергия Е=mс². Следовательно, фотон имеет импульс

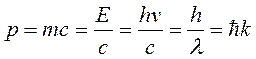. (1.3)

В соответствии с гипотезой Де Бройля формула (1.3) применима для любых частиц, в том числе движущихся со скоростями v, меньше чем скорость света, т.е.

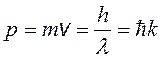(1.4)

Из формулы (1.4), называемой формулой Де Бройля, определяется длина волны Де Бройля l _ДБ материальной частицы массой m, движущейся со скоростью v:

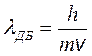(1.5)

С гипотезы Де Бройля, которая была экспериментально подтверждена опытами по дифракции электронов при отражении от поверхности анода в 1923 г., началось построение математического аппарата волновой механики, впоследствии названной квантовой механикой.

Во-первых, корпускулярно-волновой дуализм позволил объяснить постулат, введенный Бором для стационарных орбит атома. Действительно, если по замкнутой траектории – орбите электрона в атоме, распространяется волна, то длина орбиты L_орб (в соответствии с требованием однозначности описания движения электрона волной) должна составлять целое число длин волн. Тогда момент импульса электрона с учетом (1.4) можно представить в виде:

,

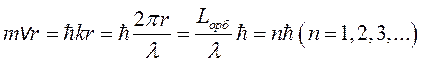который и был использован Н. Бором для вывода формулы Бальмера и постоянной Ридберга.

В основе квантовой механике лежит представление о том, что движение всякой свободно движущейся частицы описывается движением плоской волны (волновой функцией) вида

, (1.6)

где 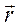– радиус-вектор произвольной точки пространства; t – время. Частота этой волны w и её волновой вектор 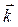связаны с энергией и импульсом частицы соотношениями

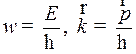
Подставляя эти соотношения в (1.4), получим в явном виде связь волновой функции с корпускулярными параметрами частицы – энергией и импульсом:

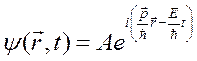. (1.7)

Такая волновая функция называется волновой функцией Де Бройля, величина А – амплитудой, а величина 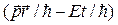– фазой волновой функции.

Физический смысл волновой функции был понят не сразу. С 30-х гг. утвердилась так называемая «копенгагенская» концепция, основанная на интерпретации экспериментов по дифракции электронов.

Проведем мысленный эксперимент по дифракции электрона на малом отверстии, сравнимым по диаметру с длиной волны Де Бройля. Будем выпускать по одному электрону и наблюдать на экране за отверстием место попадания электрона. Распределение частоты попаданий электронов должно совпадать с дифракционной картиной для плоской волны, имеющей длину волны Де Бройля. Тогда интенсивность волны Де Бройля

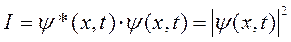
в точке экрана х в момент времени t определяет вероятность обнаружить частицу в этом месте в момент времени t. Точнее, функция

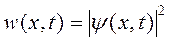
является плотностью вероятности, а полная вероятность W обнаружить частицу в объеме V в момент времени t выражается формулой

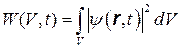
. (1.8)

Очевидно, что интеграл (1.8) по всему пространству (R^{( 3)}) отражает достоверное событие ¾ нахождение частицы где-нибудь в пространстве, поэтому

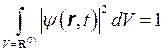. (1.9)

Условие (1.9) называется условием нормировки волновой функции, а функция y, удовлетворяющая этому условию, называется нормированной. Таким образом, волны Де Бройля ¾ суть волны вероятности нахождения частицы в данный момент времени в данном месте.

Однако при таком описании свободной частицы возникают три трудности.

Во-первых, для функции вида (1.7) интеграл нормировки (1.9) расходится. В этом случае говорят, что волновая функция нормирована на d-функцию.

Во-вторых, фазовая скорость волны Де Бройля не совпадает со скоростью частицы. Так, нерелятивистская частица, движущаяся равномерно и прямолинейно со скоростью v, имеет энергию

,

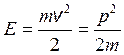а фазовая скорость волны Де Бройля

,

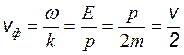т.е. меньше скорости частицы в два раза. Для релятивистской частицы, имеющей энергию

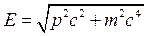
фазовая скорость волны Де Бройля

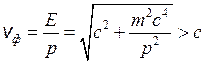
превышает скорость света.

В-третьих, поскольку волна Де Бройля не ограничена в пространстве, она не несет информации об области локализации частицы.

Указанные трудности устраняются введением описания частицы с помощью так называемого «волнового пакета», который является суперпозицией плоских волн Де Бройля:

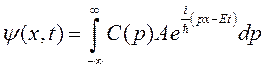, (1.10)

где С(р) - весовая функция, которая должна устранить отмеченные трудности. Определим требования к этой функции. Рассмотрим условие нормировки (1.9) с функцией вида (1.10):

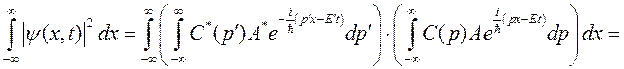
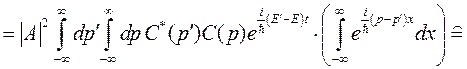
Учитывая определение δ-функции

,

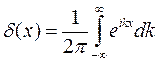последнее равенство можно продолжить в виде:

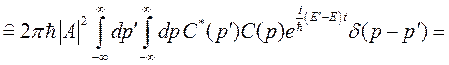
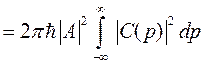
Пусть , тогда для нормировки на единицу необходимо, чтобы

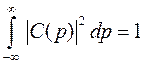. (1.11)

Тогда вероятность того, что импульс частицы заключен в интервале (р, р + dp), есть

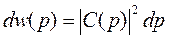(1.12)

Функция С (р) называется амплитудой вероятности того, что частица, волновая функция которой задана «волновым пакетом» (1.10), обладает импульсом р.

Выбирая выражение для волны Де Бройля в виде

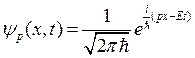, (1.13)

получим выражение для «волнового пакета»:

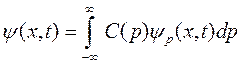. (1.14)

Рассмотрим интегральное выражение

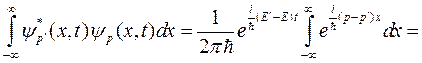
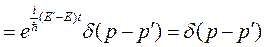. (1.15)

Полученное соотношение называется условием нормировки волн Де Бройля на δ-функцию. При р=р’, как и отмечалось ранее, квадрат модуля волны Де Бройля не сходится.

Заметим, что поскольку р и х входят в формулу для волны Де Бройля симметрично, справедливо соотношение

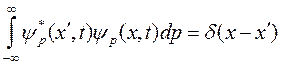, (1.16)

которое называется условием полноты.

Функция С (р) является Фурье-образом волновой функции в виде «волнового пакета». Действительно, умножим обе части (1.14) на 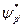и проинтегрируем по х:

,

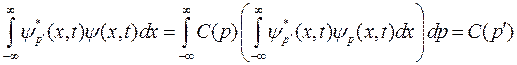а результат перепишем в виде

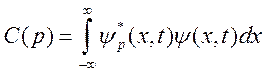(1.17)

Таким образом, волна Де Бройля ψ_р - это волновая функция состояния, которое не может осуществиться в микромире, то есть состояния свободного движения частицы со строго определенным импульсом. Но, тем не менее, такое описание частицы часто используется в приближенных расчетах.

Предположим, что «волновой пакет», описывающий свободную частицу, движущуюся со скоростью v ₀, должен быть суперпозицией плоских волн, близких по длине волны к длине волны Де Бройля (1.3). Поэтому зададим функцию С (р) в виде прямоугольника:

,

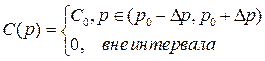где считаем Δр «p₀ = mv ₀. Тогда в окрестности р₀ зависимость энергии от импульса приближенно можно представить в виде

.

Для выбранного вида функции С (р) запишем волновую функцию (1.14) в виде:

.

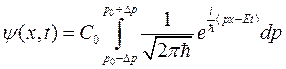Преобразуем выражение в фазе волны Де Бройля:

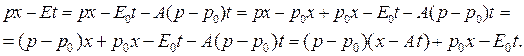
Тогда

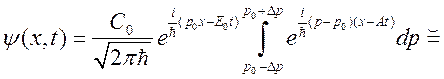
и, проводя замену переменных,

,

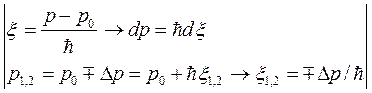получим

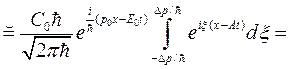
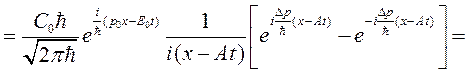
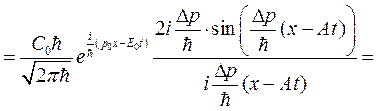
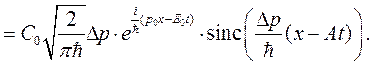(1.18)

где обозначено sinc(x)=sin(x)/ x. Вид действительной части этой волновой функции для момента времени t =0 показан на рис. 1.1.

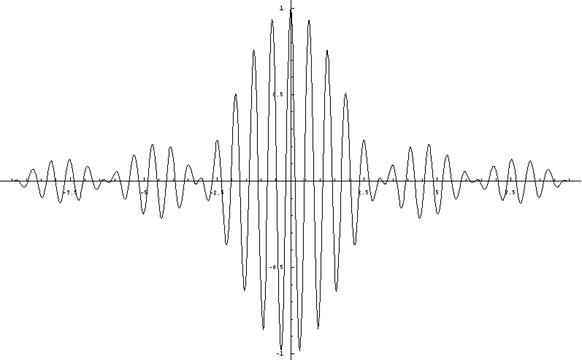
Рис. 1.1. Волновая функция свободной частицы в виде «волнового пакета».

Таким образом, волновая функция в виде «волнового пакета» определяет область наиболее вероятного расположения частицы интервалом между нулями функции sin(x), называемым главным лепестком, т.е. шириной

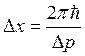. (1.19)

Групповая скорость «волнового пакета», то есть скорость движения максимума амплитуды волновой функции,

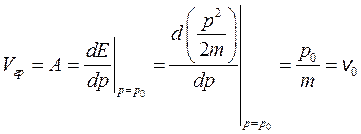
Поэтому внутри области локализации Δ х, определяемой главным лепестком функции sinc(x), волновую функцию частицы можно приближенно описывать волновой функцией Де Бройля (1.5), имея в виду, что координата частицы определена с точностью Δ х, а импульс частицы с точностью Δ р.

Date: 2015-05-19; view: 477; Нарушение авторских прав