Оптические приборы

Ход лучей в линзах. Линзой называется прозрачное тело, огра­ниченное двумя сферическими поверхностями. Линзы обычно из­готавливаются из стекла.

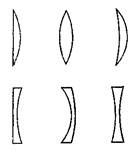
Рис.12

Тонкой называется линза, тол­щина которой значительно мень­ше радиусов ограничивающих ее сферических поверхностей. Лин­за, которая в середине толще, чем у краев, называется выпуклой линзой (рис. 12). Линза, которая у краев толще, чем в середине, называется вогнутой линзой (рис. 12). Прямая, проходящая через центры О₁ и О₂ сфериче­ских поверхностей линзы, назы­вается главной оптической осью линзы.

Если толщина линзы пренеб­режимо мала, то можно считать, что главная оптическая ось пересекается с линзой в одной точ­ке. Точка О пересечения глав­ной оптической оси с тонкой лин­зой называется оптическим цент­ром линзы.

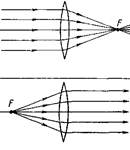
Рис.13

Опыт показывает, что луч све­та, идущий вдоль главной опти­ческой оси, проходит через линзу без изменения направления рас­пространения. В воздухе или в вакууме все лучи, параллельные главной оптической оси выпуклой линзы, после прохождения лин­зы отклоняются к оси и прохо­дят через одну точку F на глав­ной оптической оси (рис.13). Поэтому выпуклые линзы назы­вают собирающими линзами. Точ­ка F называется главным фоку­сом линзы. Плоскость, проходя­щая через главный фокус линзы перпендикулярно главной опти­ческой оси, называется фокаль­ной плоскостью.

У линзы два главных фокуса в однородной среде расположены на одинаковых расстояниях от ее оптического центра. Расстояние от оптического центра линзы до главного фокуса называется фо­кусным расстоянием F линзы. Все лучи, проходящие через один из ее главных фокусов, выходят из линзы параллельно главной опти­ческой оси (рис. 13).

В воздухе или в вакууме все лучи, параллельные главной оп­тической оси вогнутой линзы, отклоняются от оптической оси, поэтому вогнутые линзы назы­ваются рассеивающими линзами. Продолжения лучей в противопо­ложную сторону сходятся в од­ной точке F на главной оптиче­ской оси перед линзой (рис. 14). Эта точка называется главным фокусом рассеивающей линзы. Главный фокус рассеивающей линзы мнимый, так как в дейст­вительности лучи света в нем не собираются.

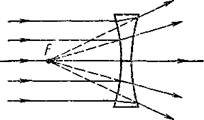
Рис.14

Построение изображений в тонких линзах. Основное свойство линз, используемое в оптических приборах, заключается в том, что все лучи, исходящие из од­ной точки А перед линзой, со­бираются в другой точке А₁ за линзой (рис. 14) или кажутся ис­ходящими из одной точки А₂ пе­ред линзой (рис. 15). В первом случае изображение точки А на­зывается действительным, во вто­ром — мнимым.

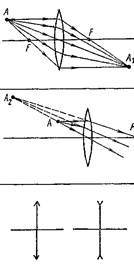
Рис.15

Замечательным свойством све­товых лучей является свойство обратимости: луч, направленный противоположно лучу, выходяще­му из любой оптической систе­мы, пройдет через нее в обрат­ном направлении точно по тому же пути, по какому прошел ее в прямом направлении первый луч.

Используя свойства лучей, проходящих через оптический центр линзы или через ее фокусы, а также лучей, параллельных главной оптической оси или од­ной из ее побочных осей, можно построить изображение любого предмета, получаемое с помощью собирающей или рассеивающей линзы. Условное изображение со­бирающей и рассеивающей линз представлено на рисунке 15.

Формула линзы. Расстояние f от собирающей линзы до изоб­ражения связано с расстоянием d, от предмета до линзы и фокусным расстоянием F линзы. Выразим эту зависимость мате­матически. Ход лучей представ­лен на рисунке 16.

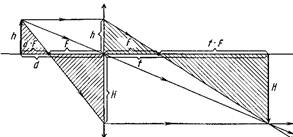
Рис 16

Из подобия треугольников (заштрихованы одинаково) следует, что

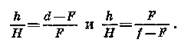
Из этих двух уравнений будем иметь

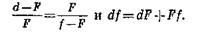
Делением на произведение d×f×F получаем

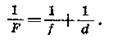
Это уравнение называется фор­мулой линзы.

Формула линзы применима для нахождения расстояния до изображения при любом распо­ложении предмета относительно линзы.

Если значение расстояния f получается при расчете отрица­тельным, то это значит, что изображение предмета мнимое и на­ходится по ту же сторону от лин­зы, что и предмет. Для рассеи­вающей линзы значение фокус­ного расстояния в расчетах нуж­но брать со знаком «минус» и, так как изображение предмета получаем мнимым, расстояние f до изображения всегда должно быть со знаком «минус».

Оптическая сила линзы. Вели­чина, обратная фокусному рас­стоянию F, называется оптичес­кой силой линзы D:

Оптическая сила выражается в диоптриях (дптр). Линза с фо­кусным расстоянием 1 м обладает оптической силой в 1 дптр. Оптическая сила, собирающей линзы положительна, оптическая сила рассеивающей линзы отри­цательна.

Линейное увеличение. В за­висимости от положения предме­та относительно линзы линейные размеры изображения изменяются. Отношение линейных разме­ров Н изображения к линей­ным размерам и предмета назы­вается линейным увеличением Г:

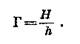
Из подобия треугольников, за­штрихованных на рисунке 17, следует

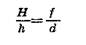
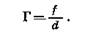
Или

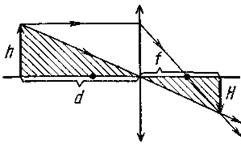
Рис.17

Из формулы линзы и последней формулы линейного увеличения Г или построением хода лучей можно установить, что для собирающей линзы при условии d > 2F дейст­вительное изображение получа­ется уменьшенным (Г<1). В слу­чае d = 2F линейные размеры действительного изображения равны размерам предмета (Г = 1). В случае F <d<2F изображе­ние действительное, увеличенное (Г>1).

При помещении предмета между фокусом и центром линзы (d<F) изображение получается увеличенное, мнимое.

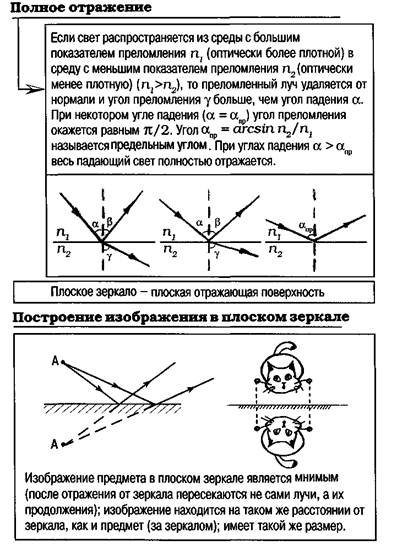
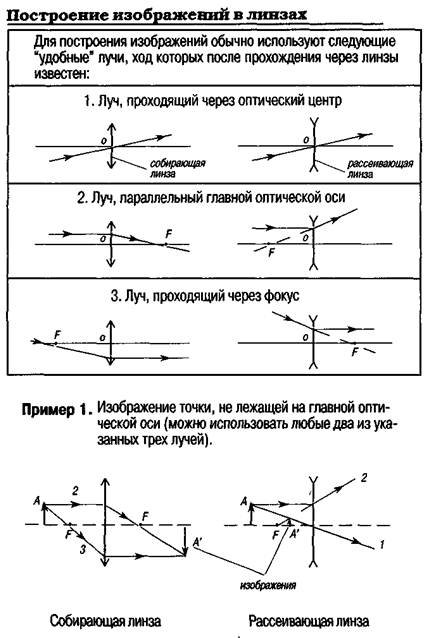
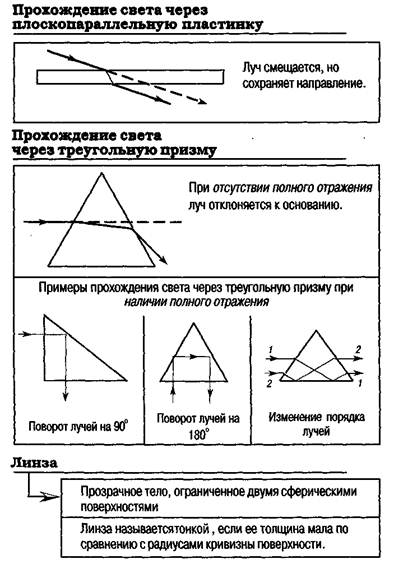
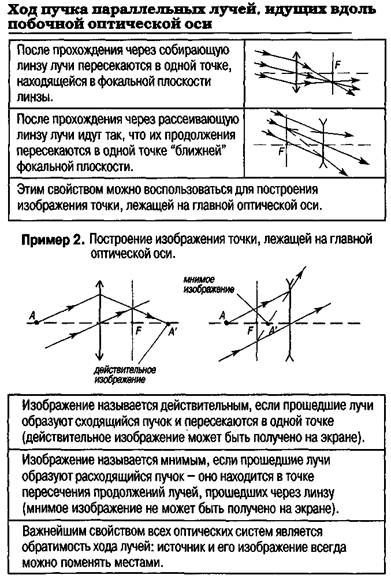
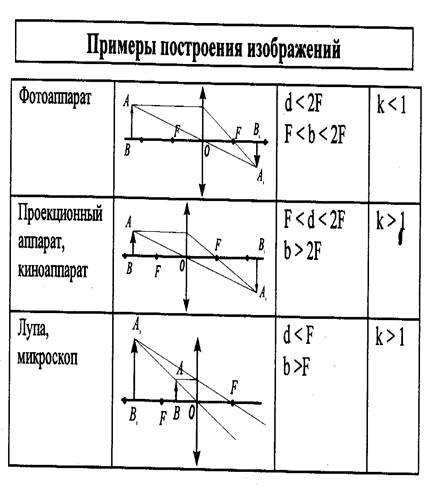
ГЛАВА II. ОПТИКА В ТАБЛИЦАХ И СХЕМАХ

Date: 2015-05-19; view: 658; Нарушение авторских прав