
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Спектральные серии атома водорода
|
|
Исследования спектров излучения разреженных газов (т.е. спектров излучения отдельных атомов) показали, что каждому газу присущ определенный линейчатый спектр, состоящий из отдельных спектральных линий или групп близко расположенных линий. Особенно отчетливо это проявляется в спектре простейшего атома водорода.
Швейцарский ученый И.Бальмер подобрал эмпирическую формулу, описывающую все известные в то время спектральные линии атома водорода в видимой области спектра:
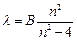 (8.1).
(8.1).
где В =const, n =3;4;5;6.
Если введем обозначение 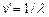 - волновое число, тогда:
- волновое число, тогда:
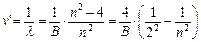 (8.2),
(8.2),
где 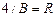 =1,10.107 м-1 – постоянная Ридберга.
=1,10.107 м-1 – постоянная Ридберга.
Из выражений (8.1) и (8.2) вытекает, что спектральные линии, отличающиеся различными значениями n, образуют группу или серию линий, называемую серией Бальмера:
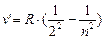 (8.3),
(8.3),
где n =3;4;5;6.
С увеличением n линии серии сближаются; волновые числа 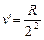 (при n®¥),
(при n®¥), 
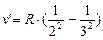 определяют границы спектральной серии.
определяют границы спектральной серии.
Наряду с серией Бальмера в спектре атомарного водорода были обнаружены другие серии, волновые числа которых можно представить аналогичными формулами.
В ультрафиолетовой области серия Лаймана:
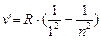 n = 2;3… (8.4)
n = 2;3… (8.4)
В инфракрасной области:
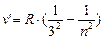 - серия Пашена, n =4;5…
- серия Пашена, n =4;5…
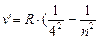 ) - серия Брэкета, n = 5;6… (8.5)
) - серия Брэкета, n = 5;6… (8.5)
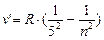 - серия Пфунда, n = 6;7…
- серия Пфунда, n = 6;7…
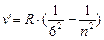 - серия Хемфри, n = 7;8…
- серия Хемфри, n = 7;8…
Анализируя соотношения (8.3) – (8.5), можно сказать, что все серии атомарного водорода можно представить общей формулой, называемой обобщенной формулой Бальмера:
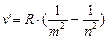 (8.6)
(8.6)
где m имеет в каждой данной серии постоянное значение, m =1;2;3;4;5;6 (определяет серию); а n = m +1, m +2,… (определяет отдельные линии этой серии). Обозначим величины 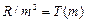 и
и 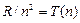 – спектральные термы. Тогда (8.6) запишется
– спектральные термы. Тогда (8.6) запишется 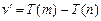 (8.7).
(8.7).
Соотношение (8.7) получило название комбинационный принцип.
Этот принцип был установлен опытным путем, а теория Бора дала ему толкование: каждому спектральному терму соответствует определенное стационарное состояние атома и 2–ой постулат Бора – это есть комбинационный принцип, выраженный иным способом. Действительно, т.к. 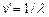 , а
, а 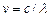 , то
, то 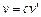 . По второму постулату Бора
. По второму постулату Бора 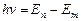 или
или 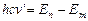 ,
,
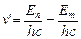 (8.8).
(8.8).
Сравнивая (8.7) и (8.8) можно записать:
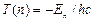 и
и 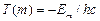 .
.
Отсюда получается выражение для энергии стационарного состояния атома: 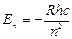 (8.9)
(8.9)
Знак «–» имеет условное значение, чисто физический смысл – энергия электрона в поле положительного ядра отрицательна. Из (8.9) видно, что энергия стационарных состояний образует дискретный ряд при n=1;2;3…
§ 9. Теория атома водорода по Бору.
Постулаты, выдвинутые Бором, позволили рассчитать спектр атома водорода и водородоподобных систем (систем, состоящих из ядра с зарядом Ze и одного электрона (например, ионы Не +, Li+), а также теоретически вычислить постоянную Ридберга.
Следуя Бору, рассмотрим движение электрона в водородоподобной системе, ограничиваясь круговыми стационарными орбитами. Потенциальная энергия взаимодействия электрона с ядром:
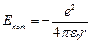 (9.1),
(9.1),
r – радиус орбиты. Кинетическая энергия электрона, движущего вокруг ядра: 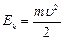 (9.2).
(9.2).
Тогда полная энергия атома:
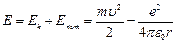 (9.3).
(9.3).
Электрон вокруг ядра движется с ускорением 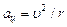 под действием кулоновской силы:
под действием кулоновской силы: 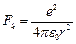 .
.
По второму закону Ньютона (ma = Fk) можно записать:
 (9.4);
(9.4);
отсюда 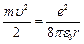 (9.5).
(9.5).
Поставим (9.5) в (9.3): 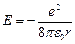 (9.6).
(9.6).
По классической механике радиус орбиты электрона может принимать любые значения, тогда и энергия согласно (9.6) может принимать любые значения. Согласно же постулатам Бора энергия атома, а значит и радиус орбиты электрона определенные. Бор предложил правило отбора или правило квантования (третий постулат Бора): из всех возможных орбит электрона осуществляется только те, для которых момент импульса электрона кратен постоянной Планка:
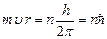 (9.7),
(9.7),
где n =1,2,3,… – главное квантовое число. Используя соотношения (9.4) и (9.7) определим радиус стационарной орбиты электрона:
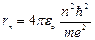
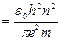 (9.8),
(9.8),
при 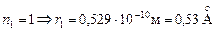 (радиус первой орбиты).
(радиус первой орбиты).
Из (9.8) следует 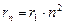 . Подставляя (9.8) в (9.10) получим выражение для энергии стационарных состояний:
. Подставляя (9.8) в (9.10) получим выражение для энергии стационарных состояний:
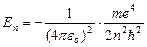 =
= 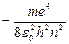 (9.9)
(9.9)
При 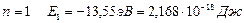 – энергия первого стационарного состояния.
– энергия первого стационарного состояния.
В состоянии с энергией Е1 атом может находиться сколь угодно долго. Для того, чтобы ионизировать атом водорода, т.е. оторвать от него электрон, ему нужно сообщить энергию 13,55 эВ.
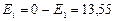 эВ;
эВ; 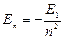 ;
;
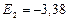 эВ;
эВ; 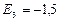 эВ;
эВ; 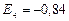 эВ и т.д.
эВ и т.д.
Состояние 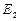 ,
, 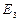 ,… соответствуют возбужденному атому. Время жизни в этих состояниях имеет порядок
,… соответствуют возбужденному атому. Время жизни в этих состояниях имеет порядок 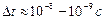 . За это время электрон успевает совершить около 100 млн. оборотов вокруг ядра.
. За это время электрон успевает совершить около 100 млн. оборотов вокруг ядра.
Придавая n различные целочисленные значения, получим для атома водорода, согласно формуле (9.9), возможные уровни энергии. Энергия атома водорода с увеличением п возрастает и энергетические уровни сближаются к границе, соответствующей значению п=¥. Атом водорода обладает, таким образом, минимальной энергией (Е1=–13,55 эВ) при n =1 и максимальной (Е¥=0) при п = ¥. Следовательно, значение Е¥=0 соответствуетионизацииатома (отрыву от него электрона). Согласно второму постулату Бора, при переходе атома водорода из стационарного состояния n в стационарное состояние т с меньшей энергией испускается квант: 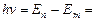
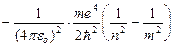 ,
,
откуда частота излучения: 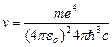
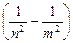 =R
=R 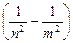 , (9.10)
, (9.10)
где 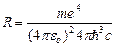 .
.
Воспользовавшись при вычислении R современными значениями универсальных постоянных, получим величину, совпадающую с экспериментальным значением постоянной Ридберга в эмпирических формулах для атома водорода: 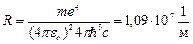 .
.
Это совпадение доказывает правильность полученной Бором формулы для энергетических уровней водородоподобной системы.
Подставляя, например, в формулу (9.10) т=1 и п=2, 3, 4,..., получим группу линий, образующих серию Лаймана и соответствующих переходам электронов с возбужденных уровней (п= 2, 3, 4,...) на основной (т= 1 ). Аналогично, при подстановке т= 2, 3, 4, 5, 10 и соответствующих им значений n получим серии Бальмера, Пашена, Брэкета, Пфунда и Хэмфри (часть из них схематически представлена на рис.9.1.). Следовательно, по теории Бора, количественно объяснившей спектр атома водорода, спектральные серии соответствуют излучению, возникающему в результате перехода атома в данное состояние из возбужденных состояний, расположенных выше данного.
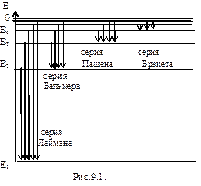 Теория Бора показала неприменимость классической физики к внутриатомным явлениям и необходимость применения квантовых законов в микромире. Но попытка построить аналогичную теорию для атома гелия потерпела неудачу. Теория Бора не была ни последовательно классической, ни последовательно квантовой теорией. Недостатки теории Бора могли быть устранены путем создания новой квантовой теории, в которой поведение и движение микрочастиц подчиняется своим законам. Это было осуществлено при создании квантовой механики.
Теория Бора показала неприменимость классической физики к внутриатомным явлениям и необходимость применения квантовых законов в микромире. Но попытка построить аналогичную теорию для атома гелия потерпела неудачу. Теория Бора не была ни последовательно классической, ни последовательно квантовой теорией. Недостатки теории Бора могли быть устранены путем создания новой квантовой теории, в которой поведение и движение микрочастиц подчиняется своим законам. Это было осуществлено при создании квантовой механики.
§ 10. Квантовые числа. Принцип Паули.
Строение электронных оболочек атома.
Состояние электрона в атоме характеризуется не одним, а несколькими квантовыми числами.
Первое их квантовых чисел – главное квантовое число: n = 1; 2;3,… Оно определяет уровни энергии электрона в атоме: 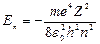 и радиусы стационарных орбит
и радиусы стационарных орбит 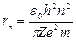 . Эти выражения вытекают из решения уравнения Шредингера и совпадают с соответствующими формулами, полученными Бором.
. Эти выражения вытекают из решения уравнения Шредингера и совпадают с соответствующими формулами, полученными Бором.
Второе квантовое число – орбитальное квантовое число  , которое при данном n может принимать значения 0, 1, 2,..., n –1. Это число определяет орбитальный момент импульса
, которое при данном n может принимать значения 0, 1, 2,..., n –1. Это число определяет орбитальный момент импульса 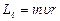 электрона относительно ядра. Момент импульса электрона в атоме квантуется по формуле:
электрона относительно ядра. Момент импульса электрона в атоме квантуется по формуле: 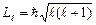
Третье квантовое число – магнитное квантовое число 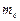 , которое при данном
, которое при данном  принимает значения 0; ±1; ±2,…, ±
принимает значения 0; ±1; ±2,…, ±  ; всего 2
; всего 2  +1 значений. Это число определяет проекции орбитального момента импульса электрона на некоторое произвольно выбранное направление Z. Возможны лишь такие ориентации вектора момента импульса
+1 значений. Это число определяет проекции орбитального момента импульса электрона на некоторое произвольно выбранное направление Z. Возможны лишь такие ориентации вектора момента импульса 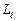 , при которых проекция
, при которых проекция 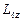 вектора
вектора 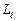 на направление внешнего магнитного поля (ось OZ) принимает значения:
на направление внешнего магнитного поля (ось OZ) принимает значения: 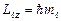
Четвертое квантовое число – спиновое (магнитное спиновое) квантовое число ms. Оно может принимать только два значения 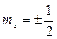 и характеризует возможные значения проекции на ось Z спина (собственного механического момента импульса)
и характеризует возможные значения проекции на ось Z спина (собственного механического момента импульса) 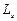 электрона:
электрона: 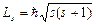 , где
, где 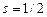 – спиновое квантовое число. Пространственное квантование спина означает, что проекция
– спиновое квантовое число. Пространственное квантование спина означает, что проекция 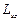 вектора спина
вектора спина 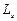 на направление внешнего магнитного поля находится по формуле:
на направление внешнего магнитного поля находится по формуле: 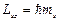 .
.
В 1924 г. швейцарский физик Паули сформулировал принцип, согласно которому: в любом атоме не может быть двух электронов, находящихся в двух одинаковых стационарных состояниях, определяемых набором четырех квантовых чисел – главного n; орбитального  ; магнитного m и спинового ms. Принципу Паули, кроме электронов подчиняются другие частицы, имеющие полуцелый спин (в единицах
; магнитного m и спинового ms. Принципу Паули, кроме электронов подчиняются другие частицы, имеющие полуцелый спин (в единицах 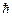 ).
).
Для электронов в атоме принцип Паули записывается таким образом: 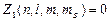 или 1,
или 1,
где 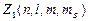 –число электронов в состоянии, характеризуемом данным набором квантовых чисел.
–число электронов в состоянии, характеризуемом данным набором квантовых чисел.
Максимальное число электронов, находящихся в состояниях, описываемых набором трех квантовых чисел n;  и m и отличающихся только ориентацией спинов электронов, равно
и m и отличающихся только ориентацией спинов электронов, равно

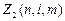 =2,
=2,
т.к. ms принимает два значения, т.е. ±1/2. Можно сказать: не может быть больше двух электронов, движение которых характеризуется одинаковыми значениями трех квантовых чисел n;  и m.
и m.
Максимальное число 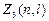 электронов, находящихся в состояниях, описываемых двумя квантовыми числами n и
электронов, находящихся в состояниях, описываемых двумя квантовыми числами n и  :
:
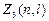 =2(2
=2(2  +1)
+1)
т. к. m принимает 2  + 1 значений,
+ 1 значений,
Определим число электронов с определенным  .
.
Электроны с  =0 называются s -электронами, их максимальное количество равно
=0 называются s -электронами, их максимальное количество равно 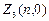 = 2(2×0+1)=2.
= 2(2×0+1)=2.
Электроны с  =1 называются р -электронами, их максимальное количество равно
=1 называются р -электронами, их максимальное количество равно 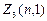 =2(2×1+1)=6.
=2(2×1+1)=6.
Электроны с  =2 называются d -электронами, их максимальное количество равно
=2 называются d -электронами, их максимальное количество равно 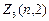 =2(2 2+1)=10.
=2(2 2+1)=10.
Электроны с  =3 называются f -электронами, их максимальное количество равно
=3 называются f -электронами, их максимальное количество равно 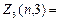 2(2×3+1)=14 и т.д.
2(2×3+1)=14 и т.д.
Максимальное число 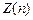 электронов, находящихся в состояниях, определяемых значением n главного квантового числа
электронов, находящихся в состояниях, определяемых значением n главного квантового числа
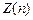 =
= 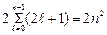
Электроны, занимающие совокупность состояний с одинаковым значением главного квантового числа n, образуют электронную оболочку. Различают следующие электронные оболочки (или слои): К-слой при n = 1; L -слой при n = 2; M -слой при n = 3; N -слой при n =4 и т.д. В каждой квантовой оболочке атома электроны распределяются по подоболочкам, соответствующим определенному значению орбитального квантового числа  ; в зависимости от
; в зависимости от  электрон находится в подгруппе с символами s, p, d, f и т.д.
электрон находится в подгруппе с символами s, p, d, f и т.д.
| Главное квантовое число | Электронная оболочка (слой) | Число электронов в состояниях | Максимальное число электронов | |||
s
( =0) =0)
| p
( =1) =1)
| d
( =2) =2)
| f
( =3) =3)
| |||
| K | – | – | – | |||
| L | – | – | ||||
| M | – | |||||
| N |
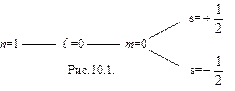 В состоянии, определяемом главным квантовым числом n = 1, могут находиться лишь два s-электрона с двумя различными ориентациями спинов (см.рис.10.1).
В состоянии, определяемом главным квантовым числом n = 1, могут находиться лишь два s-электрона с двумя различными ориентациями спинов (см.рис.10.1).
Если n = 2, то схема имеет вид, показанный на рис. 10.2.
Последовательность заполнения электронных состояний в атомах химических элементов объясняется принципом Паули.
Этот принцип дает объяснение периодичности свойств химических элементов в периодической системе, созданной Д.И.Менделеевым.
§ 11. Периодическая система элементов Менделеева.
Принцип Паули позволяет объяснить периодическую повторяемость свойств атомов. В 1869 г. Д.И.Менделеев создал периодическую систему элементов. Он показал, что если элементы расположены по порядку возрастных атомных весов за некоторым исключением, то их физические и химические свойства периодически повторяются. Это сходство распространяется и на их атомные спектры.
По теории Бора такая периодичность в свойствах элементов объясняется тем, что электроны в атомах располагаются по определенным слоям и оболочкам. Электроны, входящие в состав одного слоя, имеют одно и то же главное квантовое число. Оказалось, что каждый период таблицы Менделеева начинается с заполнения электронами нового слоя. Физико-химические свойства элементов (валентность) и оптические свойства определяются числом и расположением самых внешних валентных электронов.
Проследим построение периодической системы (или заполнение электронами слоев атома), которые подчиняются двум принципам: а) заполнение начинается с наименьшей энергии (наиболее устойчивое состояние); б) принцип запрета Паули.
Первый элемент в таблице Менделеева – атом водорода Н, для него Z = 1. Он имеет один электрон, квантовые числа для которого: n =1,  = 0, mе = 0, ms = +1/2 или –1/2, т. е. электронная конфигурация атома водорода: 1S1.
= 0, mе = 0, ms = +1/2 или –1/2, т. е. электронная конфигурация атома водорода: 1S1.
У следующего элемента гелия Не имеются два электрона, квантовые числа: n =1, 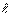 = 0, mе = 0, ms = ±1/2, т. е. электронная конфигурация атома гелия: 1S2. Слой К с числом электронов N = 2 заполнен полностью.
= 0, mе = 0, ms = ±1/2, т. е. электронная конфигурация атома гелия: 1S2. Слой К с числом электронов N = 2 заполнен полностью.
Третий элемент литий Li. Его третий электрон имеет квантовые числа: n = 2, 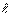 = 0, mе = 0, ms = +1/2 или – 1/2, т. е. электронная конфигурация атома 1S2 2S1.
= 0, mе = 0, ms = +1/2 или – 1/2, т. е. электронная конфигурация атома 1S2 2S1.
У берилия Ве: Z = 4 электронная конфигурация атома 1S2 2S2.
У последующих шести элементов происходит заполнение оболочек 2р. В результате у неона Nе с Z = 10 электронная конфигурация атома 1S2 2S2 2Р6, т.е. L – слой полностью заполнен и на этом заканчивается второй слой периодической таблицы. Не, Nе, а также другие атомы, в которых s- или s- и p-подгруппы полностью заняты электронами, по свойствам аналогичны и химически инертны.
| Z | символ элемента | Название элемента | Электронная конфигурация |
| Н | водород | 1s1 | |
| Не | гелий | 1s2 | |
| Li | литий | 1s1 2s1 | |
| Be | бериллий | 1s22s2 | |
| B | бор | 1s22s22p1 | |
| C | углерод | 1s22s22p2 | |
| N | азот | 1s22s22p3 | |
| O | кислород | 1s22s22p4 | |
| F | фтор | 1s22s22p5 | |
| Ne | неон | 1s22s22p6 | |
| Na | натрий | 1s22s22p63s1 | |
| Mg | магний | 1s22s22p63s2 | |
| Al | алюминий | 1s22s22p63s23р1 | |
| Si | кремний | 1s22s22p63s23р2 | |
| Р | фосфор | 1s22s22p63s23р3 | |
| S | сера | 1s22s22p63s23р4 | |
| Cl | хлор | 1s22s22p63s23р5 | |
| Ar | аргон | 1s22s22p63s23р6 |
Нарушения при заполнении слоев наблюдаются у элемента с Z=19 (калий К), где начинается заполнение оболочки 4s при незаполненной 3d:
| К | калий | 1s22s22p63s23р64s1 | |
| Сa | кальций | 1s22s22p63s23р64s2 | |
| Sc | скандий | 1s22s22p63s23р63d14s2 | |
| Ti | титан | 1s22s22p63s23р63d24s2 |
и т.д., пока не будет заполнена 3d-оболочка.
Это нарушение связано с взаимодействием между электронами, состояние которых характеризуется главными квантовыми числами n=3, n=4 и т.д. В результате взаимодействия возникает такое положение, что состояние с большим n, но малым 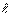 может быть энергетически более выгодным.
может быть энергетически более выгодным.
Аналогичная ситуация наблюдается у редкоземельных элементов, или лантаноидов (атомов с номерами 58-71), у которых заполнены оболочки 5s, 5р, 6s при незаполненной 4 f оболочке. У них у всех внешняя оболочка 6s2. Еще одно отступление относится к актиноидам (атомов с номерами 90-103), у которых заполняются 5 f оболочка после заполнения внешней оболочки 7s2.
Date: 2015-05-19; view: 962; Нарушение авторских прав