Волновая функция и ее физический смысл

Из содержания предыдущих двух параграфов следует, что с микрочастицей сопоставляют волновой процесс, который соответствует ее движению, поэтому состояние частицы в квантовой механике описывают волновой функцией, которая зависит от координат и времени y(x,y,z,t). Конкретный вид y -функции определяется состоянием частицы, характером действующих на нее сил. Если силовое поле, действующее на частицу, является стационарным, т.е. не завися­щим от времени, то y -функцию можно представить в виде произведения двух сомножителей, один из которых зависит от времени, а другой – от координат:

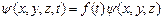(3.1)

В дальнейшем будем рассматривать только стационарные состояния. y-функция является вероятностной характеристикой состояния частицы. Чтобы пояснить это, мысленно выделим достаточно малый объем , в пределах которого значения y-функции будем считать одинаковыми. Тогда вероятность нахождения dW частицы в данном объ­еме пропорциональна ему и зависит от квадрата модуля y-функции (квадрата модуля амплитуды волн де Бройля): (3.2)

Отсюда следует физический смысл волновой функции: . (3.3)

Квадрат модуля волновой функции имеет смысл плотности вероят­ности, т.е. определяет вероятность нахождения частицы в единичном объеме в окрестности точки с координатами х, у, z.

Интегрируя выражение (3.2) по объему, определяем вероятность нахождения частицы в этом объеме в условиях стационарного поля: (3.4)

Если известно, что частица находится в пределах объема V, то инте­грал выражения (3.4), взятый по объему V, должен быть равен единице: 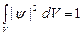(3.5)

Date: 2015-05-19; view: 518; Нарушение авторских прав