Гипотеза де-Бройля. Волны де-Бройля

КВАНТОВАЯ ФИЗИКА

Предисловие.

Предлагаемое учебное пособие предназначено для организации самостоятельной и аудиторной работы на лекционных и семинарских занятиях по курсу общей физики со студентами физико-математического факультета педагогического вуза. Оно написано по разделу “Квантовая физика” в соответствии с государственными образовательными стандартами высшего профессионального образования для специальности «032200.00 – физика с дополнительной специальностью» по физике для педвузов и является обобщением опыта лекционной работы автора. Материал распределен по пяти темам, изучаемым в данном разделе курса общей физики: волновые свойства частиц, элементы квантовой механики; атом водорода по Резерфорду-Бору; элементы физики излучения; физика атомного ядра; элементарные частицы. Пособие не исключает работу с учебниками для вузов, более того, ряд вопросов в него не вошли в связи с дефицитом лекционного времени. Например, в пособие не включен материал по квантованию момента импульса, туннельный эффект, эффект Штарка, элементы квантовой статистики и др. Изучение этих тем предусмотрено на семинарских и практических занятиях. Данное пособие может быть также рекомендовано и для студентов других специальностей физико-математического факультета с ограниченным число часов по физике, а также студентов заочной формы обучения. В данном случае предполагается возможность части материала пособия для самостоятельного изучения.

I. ВОЛНОВЫЕ СВОЙСТВА ЧАСТИЦ.

ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ

Гипотеза де-Бройля. Волны де-Бройля.

Дифракция электронов.

Французский ученый Луи де Бройль, развивая представления о двойственной корпускулярно-волновой природе света, выдвинул в 1923 году гипотезу об универсальности корпускулярно-волнового дуализма. Де Бройль утверждал, что между свойствами света и свойствами материальных частиц существует глубокая аналогия, следовательно материальные частицы обладают также двойственной природой, т.е. в определенных условиях проявляются их волновые свойства.

Как известно из оптики, квант света – фотон, кроме энергии 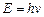характеризуется импульсом : 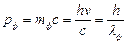; так как . Следовательно, длина волны фотона:

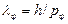(1.1)

Де-Бройль постулировал, что частице с импульсом 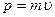соответствует длина волны: 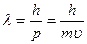(1.2)

Это соотношение (формула де Бройля) справедливо для любой частицы с импульсом р.

Вскоре гипотеза де Бройля была подтверждена экспериментально. Американские физики К.Дэвиссон и Л.Джермер в 1927 г. изучали рассеяние электронов на монокристалле никеля с помощью установки, изображенной на рис. Пучок электронов из электронной пушки 1 направлялся на кристалл никеля 2, рассеянные от кристалла электроны 3 улавливались специальным приемником 4, соединенным с чувствительным гальванометром. Интенсивность отраженного пучка определялась по силе тока, текущего через гальванометр. Опыты показали, что при заданном угле падения электроны отражаются от поверхности кристалла под различными углами, причем в одних направлениях наблюдаются максимумы числа отраженных электронов, в других – минимумы, то есть наблюдалась дифракционная картина. Это явление наблюдалось, когда длина электронной волны де Бройля 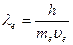имеет порядок межатомного расстояния в кристалле. Дифракционные максимумы соответствовали формуле Вульфа-Брэггов 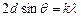, а брэгговская длина волны оказалась в точности равной длине волны, вычисленной по формуле (1.2).

Действительно, в опыте Джермера и Дэвиссона скорость электрону сообщалась в ускоряющем электрическое поле пушки: 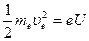. Следовательно: 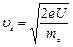. (1.3)

Поставив (1.3) в (1.2), получим: 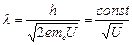, где .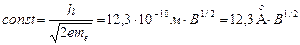

В обычных электронных приборах , следовательно, длина волны де Бройля должна иметь порядок 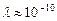м, то есть такой же, что и рентгеновские лучи, а расстояние между узлами кристаллической решетки имеет тот же порядок: 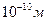. При энергии электронов 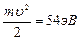получался острый максимум для угла рассеивания 50^о. По условию дифракции (формуле Вульфа-Брэггов) это соответствовало длине волны 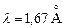и из формулы де-Бройля тоже: .

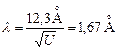Позже П.С.Тартаковский и Г.Томсон исследовали прохождение быстрых электронов через тонкие металлические пленки. При этом на фотопластинках за этими пленками получалась дифракционная картина такая же, как при дифракции рентгеновских лучей на поликристаллах.

В 1949 г. В.А.Фабрикант, Л.М.Биберман и Н.Г.Сушкин осуществили опыты по дифракции электронов с очень малой силой тока в приборе, то есть каждый электрон регистрировался фотопластинкой в случайных местах. При длительной экспозиции была получена такая же дифракционная картина, как и при короткой с большой силой тока. Это означает, что волновые свойства присущи каждому электрону в отдельности, однако дифракция одного электрона не дает всей системы точек, которая получается при дифракции от потока. След одного электрона окажется лишь в одной точке, которая разрешена условием дифракции. В этом проявляется корпускулярная природа электронов, так как электрон не может расплыться. В какое именно из мест попадет электрон, говорить нельзя. Можно говорить лишь о вероятности попадания в точку пространства.

Таким образом, электрону присуща двойственная природа, т.е. он сочетает в себе свойства и частицы, и волны. Волновая природа электронов подтверждается опытами по их дифракции. Корпускулярная природа электронов проявляется в том, что электрон действует как единое целое, не дробясь на части.

Впоследствии дифракционные явления обнаружили также для нейтронов, протонов, атомных и молекулярных пучков. Это окончательно послужило доказательством наличия волновых свойств микрочастиц и позволило описать движение микрочастиц в виде волнового процесса, характеризующегося определенной длиной волны, рассчитываемой по формуле де Бройля (1.2).

Date: 2015-05-19; view: 609; Нарушение авторских прав