Уравнение Дирака–Вейля. Не занятые в связях электроны подрешеток A и B движутся согласованно друг с другом, поэтому состояние квазичастицы описывается спинором

Не занятые в связях электроны подрешеток A и B движутся согласованно друг с другом, поэтому состояние квазичастицы описывается спинором

,

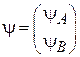где 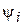– амплитуда вероятности обнаружения электрона в подрешетке .

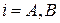Уравнение состояния. Для графена в плоскости (x, y) гамильтониан электрона

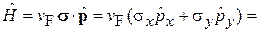
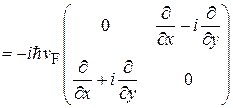, (9.1)

где

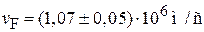- скорость Ферми;

;

, .

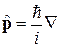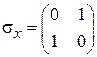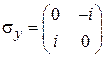Стационарное состояние с энергией Е является собственной функцией гамильтониана

.

С учетом (9.1) получаем уравнение Дирака-Вейля

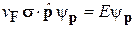. (9.2)

В явной форме

,

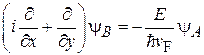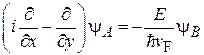. (9.3)

Состояние 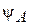, связанное с подрешеткой A, зависит от ближайшего окружения, т. е. от состояния 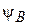подрешетки B, и наоборот.

Состояния свободного движения. Гамильтониан коммутирует с оператором импульса 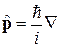, тогда решение (9.2) является плоской волной с импульсом 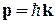. Между состояниями подрешеток A и B возможна разность фаз, поэтому решение ищем в виде спинора

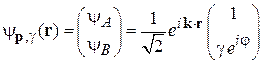. (9.9)

В декартовых координатах

,

.

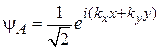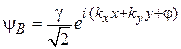Параметры γ и φ получим, подставляя (9.9) в уравнение (9.3):

,

.

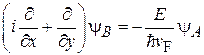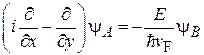Находим

,

.

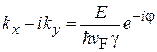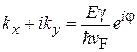Перемножение левых сторон и правых сторон уравнений дает

.

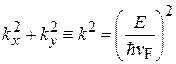Получаем дисперсионное соотношение

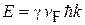, (9.10)

где

, ,

,

, ,

.

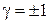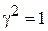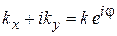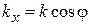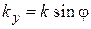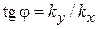Следовательно, для состояний

,

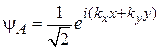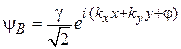
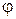- угол между импульсом 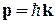и осью x;

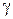– индекс зоны, в которой находится частица;

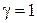соответствует электрону в зоне проводимости с энергией ;

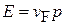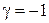соответствует дырке в валентной зоне с энергией .

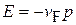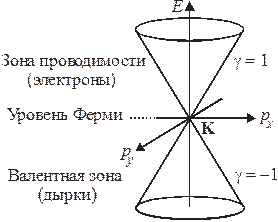
Частные случаи:

1. Импульс направлен вдоль оси x

, , ,

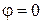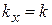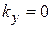тогда из

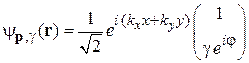
получаем

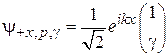, (9.11а)

2. Импульс направлен против оси x

, , , ,

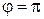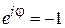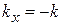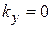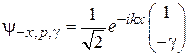, (9.11б)

3. Импульс направлен вдоль оси y

, , , ,

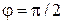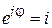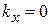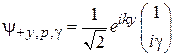. (9.11в)

4. Импульс направлен против оси y

, , , ,

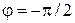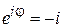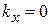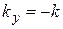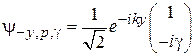. (9.11г)

Состояния удовлетворяют условиям ортогональности и нормировки

,

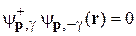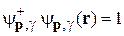. (9.12)

Date: 2015-05-19; view: 501; Нарушение авторских прав