Обменное взаимодействие

При отсутствии магнитного и спин-орбитального взаимодействия спин влияет на энергию двухчастичного состояния благодаря обменному взаимодействию, действующему на фоне любого взаимодействия между частицами.

Спиновая и координатная части волновой функции двух электронов независимые, и входят в волновую функцию сомножителями

.

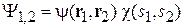Для фермионов функция Y_1,2 антисимметричная при перестановке частиц. Следовательно, если координатная функция 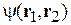симметричнаяпри перестановке частиц, то спиновая функция 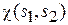антисимметричная, и наоборот.

Ранее показано, что спиновая функция двухчастичного состояния с полным спином 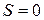антисимметричная при перестановке частиц, при 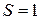– симметричная. Переход между 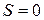и 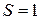происходит при повороте спина у одной частицы, и это вызывает изменение четности координатной функции. Такое влияние электронов друг на друга при любом расстоянии между ними объясняется обменным взаимодействием, действующим между перепутанными состояниями.

Четность координатной функции двух электронов. В сферической системе координат с началом в центре масс угловое состояние описывает сферическая функция 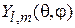, где – орбитальное число системы; 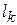– орбитальное число электрона . При взаимной перестановке частиц углы изменяются

, .

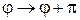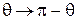Сферическая функция согласно (4.27) получает множитель

.

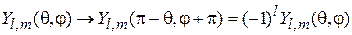Следовательно, четностькоординатной функции двух частиц

совпадает с четностью орбитального числа .

Четность спиновой функции определяется полным спином S.

При

, ,

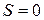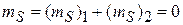состояние называется синглетным, от лат. singularis – «одиночный». Как показано ранее, спиновая функция (П.11.16)

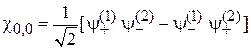
нечетная при перестановке частиц, тогда координатная функция четная и согласно (7.40)

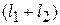– четное.

При

,

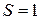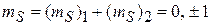
состояние называется триплетным от лат. triplex – «тройной». Спиновые функции (П.11.14), (П.11.15) и (П.11.17):

,

,

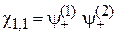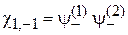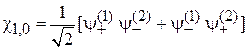
четные при перестановке частиц. Координатные функции нечетные, и

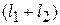– нечетное.

Существует корреляция между четностью орбитального числа двух электронов и их суммарным спином. Корреляция объясняется обменным взаимодействием.

Координатная часть волновой функции системы двух электронов

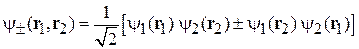(8.41)

является четной или нечетной в зависимости от спина системы S. Знак «плюс» соответствует 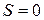, знак «минус» соответствует 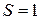. Состояние 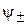является перепутанным по положениям частиц.

Обменное взаимодействие. Пусть между электронами существует немагнитное взаимодействие 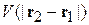, не зависящее от спина. Тип симметрии координатной части волновой функции влияет на энергию состояния, и она зависит от спина системы. Это влияние спина на энергию состояния является следствием обменного взаимодействия. Рассмотрим взаимодействие в рамках первого порядка теории возмущений.

Энергия системы в состоянии (8.41)

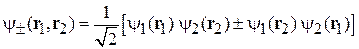
согласно (6.10) равна

,

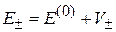где

,

,

,

,

.

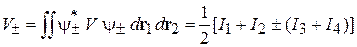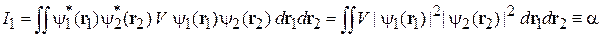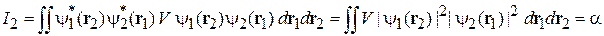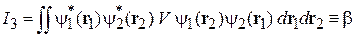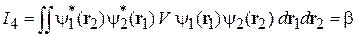Учтена симметрия интегралов при замене 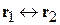. Поправка к энергии α возникает за счет взаимодействия между электроном 1, находящимся в определенной точке 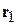, или 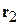, и электроном 2, находящимся в другой точке 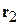, или 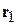. Поправка β вызвана обменным взаимодействием, когда каждый электрон присутствует одновременно в двух точках.

В результате для состояний с координатными функциями и полным спином получаем

,

,

,

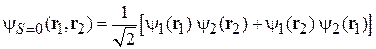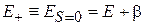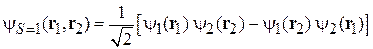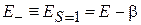, (8.42)

где

;

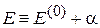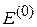– невозмущенная энергия состояния; α – энергия взаимодействия частиц, одна из которых распределена в пространстве c плотностью вероятности 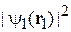, а другая – c плотностью вероятности .

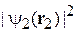Date: 2015-05-19; view: 513; Нарушение авторских прав