Уравнение Паули. В отсутствии магнитного поля спин электрона не входит в гамильтониан и в экспериментах в явной форме не проявляется

В отсутствии магнитного поля спин электрона не входит в гамильтониан и в экспериментах в явной форме не проявляется. Учет спина в волновой функции приводит, согласно (7.19), лишь к появлению постоянного множителя. В магнитном поле спиновый магнитный момент изменяет энергию системы, дает вклад в гамильтониан и уравнение Шредингера переходит в уравнение, полученное В. Паули в 1927 г.

Гамильтониан электрона в электромагнитном поле без учета спина имеет вид (5.40)

.

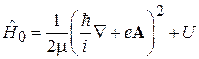Взаимодействие спина с магнитным полем с учетом (7.2), (7.5) и (7.9) дает

,

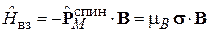где оператор спинового магнитного момента электрона

.

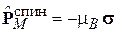Полный гамильтониан в матричной форме 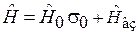получает вид

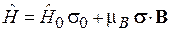, (7.20)

где

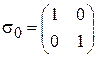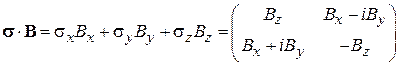, . (7.21)

Уравнение Паули. Подстановка (7.20) в уравнение Шредингера 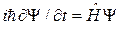дает

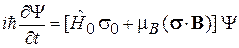, (7.22)

где 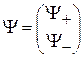; 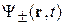– состояния с проекциями спина 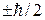на направление поля.

Однородное магнитное поле. Слагаемое 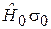в (7.22) не зависит от спина, а 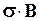не зависит от координат, поэтому спиновые и координатные переменные разделяются

,

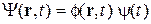где 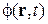– координатная функция, 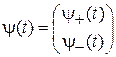– спиновая функция. Подстановка функции в (7.22) дает независимые уравнения

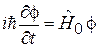, (7.23)

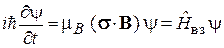. (7.24)

Взаимодействие спина с однородным магнитным полем не влияет на координатную часть волновой функции. При 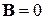спиновая функция не зависит от времени. При 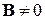из (7.24) и (7.21) для спиновых функций с противоположными проекциями спина получаем

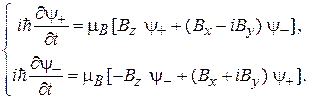(7.25)

В поле 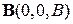уравнения разделяются

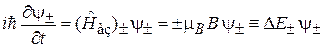, (7.26)

где ; .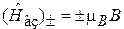

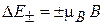Стационарное состояние. Из (7.23) и (7.26) следует, что функции состояния 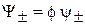удовлетворяют стационарному уравнению Шредингера

.

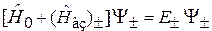Учитывая 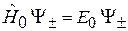и (7.26), получаем

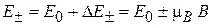. (7.27)

Если спин электрона направлен по полю, то его спиновый магнитный момент – против поля и энергия состояния увеличивается на 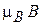.Если спин направлен против поля, то магнитный момент – по полю и энергия состояния понижается на 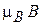. Магнитное поле расщепляет уровень энергии, снимая вырождение по спиновому числу 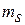. Расщепление в магнитном поле уровней атома с разными значениями магнитного квантового числа и нулевым спином описал П. Зееман в 1896 г. Спиновое расщепление (7.27) называется аномальным эффектом Зеемана.

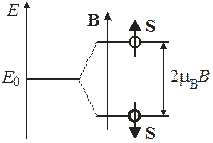
Спиновое расщепление уровня

Решения (7.26) имеют вид

, ,

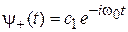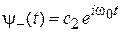где

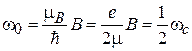, (7.28)

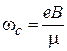– циклотронная частота, тогда получаем спиновую функцию

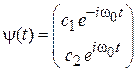(7.29)

с условием нормировки 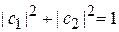. Из (7.15) 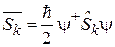находим средние проекции спина

,

,

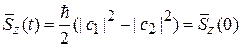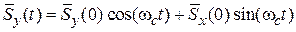. (7.30)

В постоянном магнитном поле средняя проекция спина электрона на направление поля сохраняется, вектор спина прецессирует вокруг направления поля с циклотронной частотой.

Спиновый магнитный резонанс. Взаимодействие спинового магнитного момента с магнитным полем расщепляет уровень энергии электрона на два подуровня. Периодическое возмущение двухуровневой системы вызывает переходы между уровнями с частотой Раби. Комбинированное однородное постоянное поле 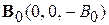, расщепляющее уровни, и периодическое поле 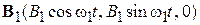, вращающееся в плоскости (x,y) с частотой w₁, позволяют управлять спиновым состоянием, т. е. получать желаемую проекцию спина, измерять магнитный момент и массу частицы.

Для частицы с положительным зарядом, спином 1/2 и магнитным моментом m₀ система уравнений (7.25) для спиновой функции 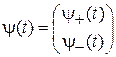имеет вид

Учитываем 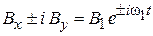и 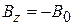, тогда

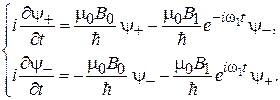(7.31)

Заменяем

, ,

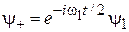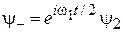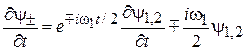
и обозначаем

,

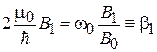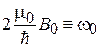
– циклотронная частота, или частота прецессии магнитного момента, или частота квантового перехода между уровнями с противоположенными направлениями магнитного момента. Из (7.31) получаем

(7.32)

Общие решения ищем в виде

, .

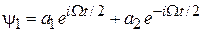Подставляем решения в (7.32), тогда второе уравнение удовлетворяется при любом t, если

, .

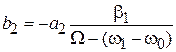Первое уравнение удовлетворяется при любом t, если

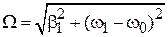(7.33)

– частота Раби. В результате

,

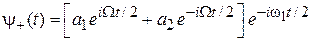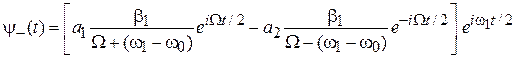(7.34)

с условием нормировки

.

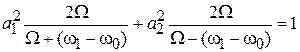Если при проекция спина положительная – 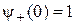, , 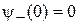то из (7.34) находим

, .

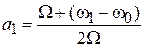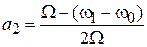При 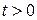решения (7.34) получают вид

,

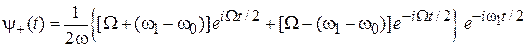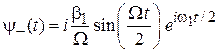. (7.35)

Вероятность перевернутого спина

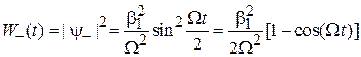. (7.36)

Проекция спина на направление постоянного магнитного поля периодически изменяется с частотой Раби. Через время 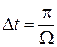спин переворачивается. Измеряя период осцилляций 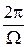, получаем магнитный момент 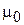частицы.

Циклотронный резонанс. Если поле В ₁ слабое 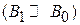и осциллирует с высокой частотой 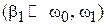, тогда из (7.33) получаем

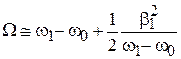, (7.37)

и вероятность переворота спина мала. Исключением является резонансная частота вынуждающего поля

,

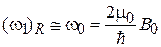совпадающая с циклотронной частотой, пропорциональной постоянному магнитному полю. Длина электромагнитной волны, вызывающей резонанс системы с 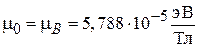и 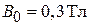, находится в СВЧ диапазоне

.

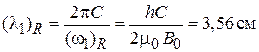Из (7.33) 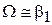и из (7.36) с учетом (7.37) находим

.

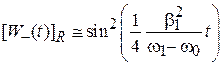Границы области резонанса определяем условием 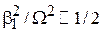, или 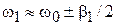, тогда ширина резонанса

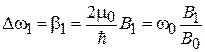
пропорциональна амплитуде осциллирующего поля. Измерив частоту 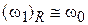наибольшего поглощения энергии вращающегося поля, по формуле циклотронной частоты (1.24) находим массу заряда. Для эксперимента необходимо, чтобы время свободного пробега заряда было достаточно большим 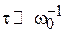, поэтому измерение эффективной массы носителя тока в кристалле требует охлаждения до низких температур.

Date: 2015-05-19; view: 886; Нарушение авторских прав