Повышающий и понижающий операторы

МОМЕНТ ИМПУЛЬСА

Динамика вращательного движения квантового объекта описывается операторами момента импульса и их собственными функциями.

Вектор момента импульса в классической механике и его проекции в декартовых координатах

,

, , ,

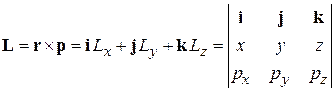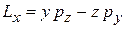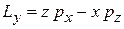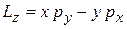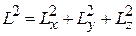. (4.1)

Выражения симметричны при циклической перестановке .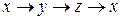

Операторы момента импульса

Декартовые координаты. Величины в (4.1) заменяем операторами и получаем оператор момента импульса

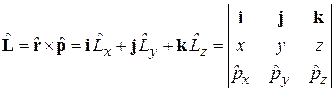, (4.2)

операторы проекций

, ,

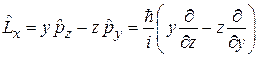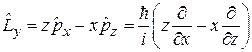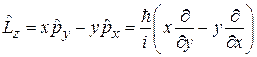, (4.3)

Оператор квадрата момента импульса

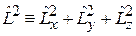. (4.4)

Перестановочные соотношения

, , ,

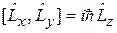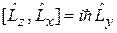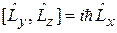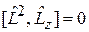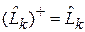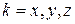, , . (4.5)

Следовательно, 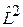и имеют одинаковый набор собственных функций.

Сферические координаты :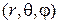

; ; ,

, , ,

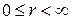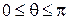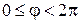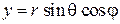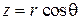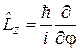, (4.6)

. (4.7)

Оператор Лапласа

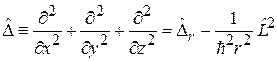, (4.8)

радиальная часть оператора Лапласа

, (4.9)

радиальный импульс

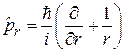, (4.9а)

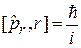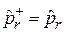, . (4.9б)

Повышающий и понижающий операторы

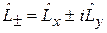, (4.10)

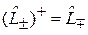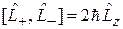, , (4.11)

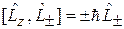, (4.12)

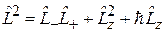. (4.13)

Сферическая функция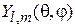

Является собственнойфункцией 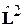и

, (4.14)

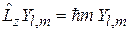, (4.15)

где 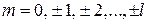– магнитное квантовое число; 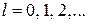– орбитальное квантовое число. Состояния 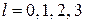обозначаются s, p, d, f (от англ. sharp – резкий, principal – главный, diffuse – расплывчатый, fundamental – фундаментальный). m и l определяют проекцию L на ось z и модуль

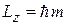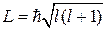, . (4.16)

Число проекций 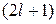. Направление L квантуется

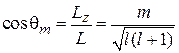. (4.17)

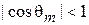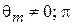, , поэтому L не может быть направлен вдоль оси z. Определенность 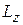приводит к неопределенностям некоммутирующих с ним 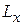и 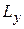, которые дают вклад в 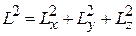, поэтому .

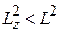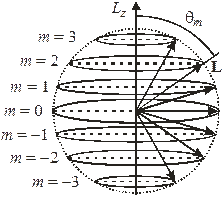
Пространственное квантование

момента импульса при l = 3

Из (4.12) и (4.15) следует

.

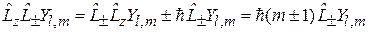Операторы 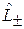переводят состояние с собственным значением m в состояния с собственными значениями 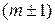, т. е. 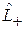повышает на единицу число m, а 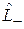понижает. Выполняется

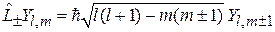, (4.18)

Выражение для сферической функции. Подстановка (4.6) в (4.15) и (4.7) в (4.14) дает дифференциальные уравнения. Переменные разделяются

.

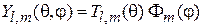Получаются уравнения и условие периодичности

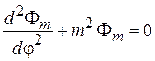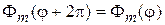, , (4.19)

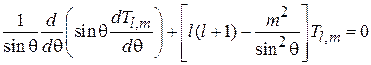. (4.20)

Из (4.19)

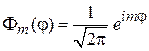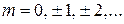, (4.21)

На основании 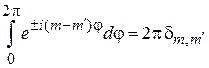выполняется условие ортонормированности

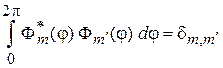. (4.22)

Уравнение (4.20) совпадает с уравнением для присоединенных функций Лежандра, тогда ,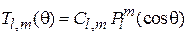

.

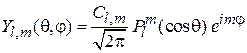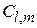определяется из условия нормировки

, .

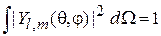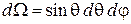При 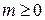получаем

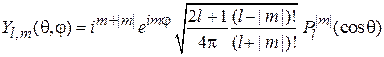. (4.23)

Выполняются

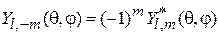, (4.24)

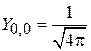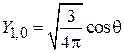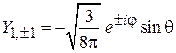, , . (4.25)

Условие ортонормированности

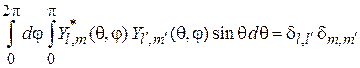. (4.26)

Инверсия координат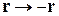

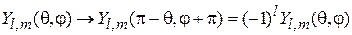. (4.27)

Четность состояния, описываемого сферической функцией, совпадает с четностью числа l.

Date: 2015-05-19; view: 3909; Нарушение авторских прав