Основные теоретические положения

Электропроводностью вещества называется величина, обратная его электрическому сопротивлению. В системе СИ электропроводность измеряется в сименсах (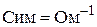). Удельная электропроводность – величина, обратная удельному сопротивлению :

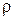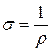. (3.1)

Металлы обладают высокой удельной электропроводностью 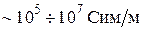. Способностью проводить электрический ток металлы обладают при всех температурах, вплоть до абсолютного нуля, причем, чем ниже температура, тем больше электропроводность металла.

Удельная электропроводность полупроводников изменяется в широких пределах 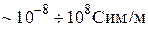. Диэлектрики обладают проводимостью, заключенной в диапазоне . Для всех неметаллических твердых тел характерен рост электропроводности с повышением температуры.

Классическая электронная теория металлов исходила из предположения, что валентные электроны не связаны с атомами, а свободно движутся по всему кристаллу, образуя электронный газ. Внешнее электрическое поле создает упорядоченное движение свободных электронов металла, то есть электрический ток. Столкновения электронов с колеблющимися ионами кристаллической решетки приводит к изменению скорости электронов и тем самым к нарушению их упорядоченного движения, чем и объяснялась причина электрического сопротивления металлов.

Теория непроводящих твердых тел опиралась на предположение о том, что кристаллические решетки этих тел состоят из положительных и отрицательных ионов, но не содержат свободных электронов, способных перемещаться под действием внешнего поля. В полупроводниковых материалах предполагалась слабая связь валентных электронов со своими атомами. Вследствие этого с ростом температуры происходит термический отрыв валентных электронов, что и обусловливает электропроводность.

Не смотря на большие успехи классической теории, оставалось много нерешенных проблем. В частности, не ясно, по какой причине в металлах электроны свободны, в полупроводниках слабо связаны, а в диэлектриках жестко связаны.

Современная теория твердого тела на основе квантовой механики объясняет всю совокупность свойств и причины различия твердых тел. При этом твердое тело необходимо рассматривать как многоядерную и многоэлектронную систему, в которой действуют электростатические силы. Однако, ни в классической, ни в квантовой теории не существует методов точного решения динамической задачи для системы многих частиц. Приближенное решение приводит к зонной теории.

Зонная теория твердых тел

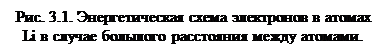
Если мысленно расположить N атомов в виде кристаллической решетки, но на большом расстоянии друг от друга, то атомы в такой системе практически не взаимодействуют и каждый электрон находится на соответствующем атомном уровне энергии («боровской орбите»). На рис. 3.1 изображены энергетические состояния электронов в атомах Li при больших межатомных расстояниях. Кривые линии изображают потенциальную энергию электрона в атоме, обусловленную его электростатическим притяжением к ядру. Горизонтальные прямые – разрешенные уровни энергии. На нижнем уровне находятся два электрона, на верхнем – один. Стрелки указывают направления спинов электронов. Для простоты на рисунке не показаны пустые воз­бужденные уровни между вторым уровнем и состояниями иони­за­ции, в которых электрон полностью отрывается от атома и потому может иметь любую энергию. Штриховкой на рис. 3.1 показан потенциальный барьер, препятствующий переходу валентного электрона от одного атома к другому.

Заселенность электронами различных уровней энергии квантовой системы (атома, молекулы или твердого тела), то есть относительное число электронов в данной системе, обладающих теми или иными значениями энергии, характеризуется распределением Ферми. Сущность этого распределения можно пояснить следующим образом. Если система, например атом, имеет только один электрон, то при температуре Т = 0 К электрон займет состояние с наименьшей энергией. Так как по принципу Паули в каждом состоянии не может находиться более одного электрона, то увеличение числа электронов в системе приводит к последовательному заполнению ими все более высоких энергетических уровней. Таким образом, при Т = 0 К в каждом состоянии с энергией E, меньшей, чем энергия верхнего заполненного уровня E_F, находится один электрон, а все состояния с бóльшими энергиями пусты. 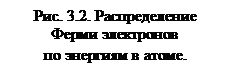Поэтому распределение Ферми при Т = 0 К имеет вид ступеньки (рис. 3.2, а). Энергия E _F последнего заполненного уровня называется энергией Ферми для Т = 0 К, а соответствующий уровень – уровнем Ферми. Чем больше число электронов в системе, тем выше расположен уровень Ферми.

При температуре, отличной от нуля, картина усложняется. Электроны с энергией, меньшей E_F, из-за теплового движения перебрасываются в состояния с энергией, большей E_F. Поэтому вероятность пребывания электрона в состоянии с энергией E > E_F становится отличной от нуля, а вероятность его нахождения в состоянии с энергией E < E_F меньше 1, ступенька сглаживается (рис. 3.2). Вероятность заполнения состояния с энергией E при любой температуре Т задается распределением Ферми:

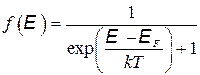, (3.2)

где k – постоянная Больцмана. Из (3.2) видно, что при E = E_F функция распределения 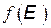= ½ при любой температуре 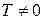. Это означает, что при отличной от абсолютного нуля температуре уровень Ферми имеет смысл энергетического уровня, вероятность заполнения которого равна ½.

Представим теперь, что решетка из разделенных атомов сжимается до реальных значений межатомных расстояний. При сближении атомов возникают несколько эффектов. На каждый электрон будет теперь действовать не только ядро собственного атома, но и ядра соседних атомов. Притягивая электрон, эти ядра ослабляют связь его в атоме, вследствие чего высота потенциального барьера, разделяющего атомы, уменьшается. Следовательно, уменьшается и энергия связи валентного электрона.

Влияние соседних атомов на валентные электроны и электроны внутренних заполненных оболочек будет различным. На электроны внутренних оболочек соседние атомы влияют незначительно, так как находятся от них гораздо дальше, чем собственное ядро атома. Тем не менее, в результате туннельного эффекта в твердом теле возникает движение электронов от атома к атому, что приводит к обобществлению всех электронов, находящихся на одном и том же атомном уровне. Вследствие соотношения неопределенностей 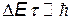, связывающего время жизни t электрона в некотором состоянии с неопределенностью его энергии 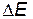(шириной уровня), туннельные переходы электронов приводят к расширению уровня энергии электрона в атоме и превращению его в кристалле в энергетическую полосу (зону) шириной 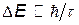. Поскольку вероятность туннелирования экспоненциально убывает с ростом высоты барьера, ширина энергетической зоны для глубоких внутренних уровней оказывается очень малой и электроны этих уровней можно считать локализованными на узлах решетки. Поэтому атомное ядро вместе со всеми внутренними электронами выступает в твердом теле как единый атомный остов – ион данного элемента.

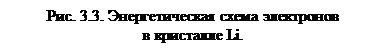
Иначе ведут себя валентные электроны. Так как потенциальные ямы соседних атомов в кристалле значительно перекрываются, атомные уровни валентных электронов обычно оказываются несколько выше потенциального барьера. В результате сами валентные электроны приобретают возможность почти свободно двигаться по кристаллу (рис. 3.3). Характер этого движения определяется периодическим потенциалом кристаллической решетки, создаваемым атомными остовами. В стационарном состоянии валентный электрон в кристалле обладает вполне определенной энергией, находится на определенном уровне энергии. Только теперь этот уровень принадлежит уже не отдельному атому, а всему кристаллу.

Взаимодействие между N атомами приводит к расщеплению уровней электронов. Число их остается прежним, равным N, но они уже не совпадают. Одни уровни смещаются вверх, другие – вниз, и уровень превращается в энергетическую зону, состоящую из N близких уровней. На рис. 3.4 показано расщепление электронных уровней лития и превращение их в энергетические зоны в кристалле. При истинном межатомном расстоянии d₀ основной уровень Е₁ практически не изменяется, тогда как валентный уровень превращается в широкую зону. Слева изображены получившиеся зоны, причем верхняя соответствует зоне валентных электронов, то есть электронов проводимости.

Состояния электронов в кристалле отличаются уже не тем, какому атому принадлежит электрон, а уровнем энергии, на котором он находится в зоне. При температуре абсолютного нуля, Т = 0 К, все уровни в заштрихованных областях зон заняты электронами, а в незаштрихованных – пусты.

Таким образом, каждому энергетическому уровню изолированного атома в кристалле соответствует зона разрешенных энергий. Зоны разрешенных энергий разделены областями запрещенных энергий – запрещенными зонами. С увеличением энергии электрона в атоме ширина разрешенных зон увеличивается, ширина запрещенных – уменьшается.

Степень заполнения электронами уровней в какой-либо энергетической зоне зависит от заполнения того атомного уровня, из которого эта зона возникла. Из пустых уровней получаются пустые зоны, из заполненных – заполненные. Если же уровень заполнен частично, то есть, например, на нем находится один электрон, как в случае лития, то из такого уровня образуется частично заполненная зона. Жирная линия внутри частично заполненной зоны на рис. 3.4 проведена так, что при любом межатомном расстоянии в рассматриваемой системе атомов лития выше и ниже нее находится по N /2 уровней. Так как наиболее устойчивым состоянием системы является такое, при котором энергия минимальна, то N валентных электронов в кристалле будут находиться в нижней половине зоны, то есть заполнять N /2 нижних уровней. Поэтому зона заполнена лишь частично.

При хаотическом тепловом движении электронов элементарные токи взаимно компенсируются. Чтобы в твердом теле возник электрический ток, нужно приложить к нему электрическое поле, которое ускорит электроны, движущиеся в одном направлении, и замедлит те электроны, которые движутся в противоположном направлении. Но ускорение и замедление электрона проявляется как изменение его энергии, то есть означает переход электрона на другой энергетический уровень. Это возможно, если в энергетическом спектре кристалла свободные уровни непосредственно прилегают к заполненным. При наложении поля происходит перераспределение электронов по уровням, возникает упорядоченное движение электронов. Такие кристаллы являются металлами.

Если же заполненные и свободные уровни разделены областью значений энергии, которых у электронов в кристалле быть не может, то слабое электрическое поле не может перевести электроны на свободные уровни, а следовательно, тока не возникает и кристаллы являются неметаллами.

Таким образом, принадлежность кристалла к металлам или неметаллам определяется характером заполнения зон. Если в его энергетическом спектре при Т = 0 есть частично заполненная зона – это металл, если спектр энергий состоит из целиком заполненных и целиком вакантных зон – это неметалл. При Т ≠ 0 в неметаллах частично заполненные уровни возникают в двух зонах – самой нижней из тех, которые при Т = 0 были пусты, и в прилежащей снизу зоне, которая при Т = 0 была целиком заполнена. Первая из них называется зоной проводимости, вторая – валентной зоной. Энергетический промежуток между этими зонами называется запрещенной зоной.

Из приведенных рассуждений становится понятно, что в твердом состоянии будут металлами, прежде всего, элементы с нечетной валентностью. Действительно, для твердых тел, в элементарной ячейке которых содержится только один атом, число уровней в каждой зоне равно числу атомов в кристаллической решетке. Для заполнения всех состояний зоны на ее уровнях должно находиться 2 N электронов, то есть, четное число. Но в атомах элементов, принадлежащих к нечетным группам периодической системы, содержится нечетное число валентных электронов. Следовательно, одна из зон кристалла, состоящего из таких атомов, будет заполнена лишь частично и такой кристалл должен обладать металлическими свойствами.

В сложных кристаллических решетках такая простая картина нарушается. Например, трехвалентный бор является диэлектриком, поскольку он имеет сложную кристаллическую структуру, в которой все зоны оказываются заполненными, так как в элементарной ячейке его решетки число атомов четное. Аналогично, в ряде случаев элементы с четной валентностью являются проводниками. Это объясняется тем, что близкие друг к другу уровни расщепляются настолько сильно, что получающиеся из них зоны перекрываются. В результате возникает единая зона, часть уровней которой занята, а часть свободна.

Многочисленные металлические сплавы также являются проводниками. Природа электропроводности сплавов та же, что у чистых металлов. При изменении состава сплава изменяется степень заполнения электронами уровней энергии. В ряде случаев при определенных соотношениях концентраций компонентов происходит изменение кристаллической структуры сплава. При изменении состава сплава в пределах неизменной структуры степень ее упорядоченности также оказывается неодинаковой: чем сильнее отличается состав сплава от однокомпонентного, тем больше искажений в кристаллической решетке. Все эти факторы приводят к тому, что электрическое сопротивление сплавов обычно больше, чем у чистых металлов.

Электрический ток представляет собой направленное движение электрических зарядов. Подвижными носителями заряда в металлах являются электроны, в полупроводниках – электроны и дырки, в растворах электролитов – ионы. Плотность тока 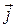связана с напряженностью электрического поля в среде 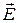посредством соотношения:

,

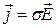называемого дифференциальной формой закона Ома. Если в веществе одновременно присутствуют подвижные носители заряда двух знаков, то электропроводность складывается из электропроводности положительных носителей 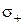и отрицательных носителей 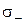. В этом случае:

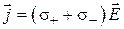. (3.3)

Плотность тока 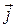может быть представлена через концентрацию свободных носителей , их заряд 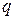и скорость упорядоченного движения :

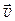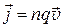. (3.4)

Из дифференциальной формы закона Ома и (3.4) находим:

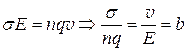. (3.5)

Величину 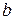называют подвижностью носителей заряда. Из (3.3) и (3.5) находим:

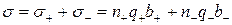. (3.6)

Электропроводность металлов

Предположим, что n – концентрация свободных электронов в металле. Двигаясь в кристаллической решетке, электрон получает энергию от поля 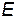и растрачивает ее на столкновения с решеткой. В результате устанавливается некоторая стационарная скорость 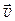в направлении, противоположном полю, при которой электрон отдает решетке столько энергии, сколько получает от поля. Эту скорость электронов называют дрейфовой скоростью или скоростью дрейфа.

Запишем уравнение движения для электрона в металле:

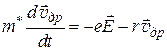, (3.7)

где 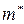– эффективная масса электрона, 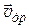– дрейфовая скорость электронов, 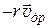– слагаемое, описывающее силу «трения», действующую на электрон. Эффективная масса описывает инерционные свойства электрона в периодическом поле кристаллической решетки. Приписывая электрону, находящемуся в периодическом поле кристалла, массу 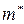, можно считать этот электрон свободным и описывать его движение как движение свободной частицы.

После выключения внешнего поля 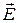дрейфовая скорость будет убывать. Действительно, при 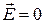, уравнение (3.7) переходит в:

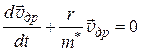. (3.8)

Решение (3.8) имеет вид:

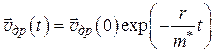. (3.9)

Из (3.9) следует, что за время 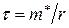значение дрейфовой скорости уменьшается в e раз. Время 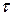является характерным временем установления равновесия между электронами и решеткой, нарушенного действием внешнего электрического поля.

Установившееся значение дрейфовой скорости можно найти, приравняв нулю сумму электрической силы и силы трения:

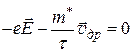. (3.10)

Отсюда

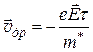. (3.11)

Из соотношения (3.5) с использованием (3.11) находим выражение для плотности тока и удельной электропроводности:

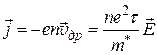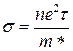, . (3.12)

В реальных кристаллах геометрическая периодичность нарушается как дефектами структуры решетки (атомы в междоузлиях, примеси, пустые узлы и т.п.), так и тепловыми колебаниями решетки. Все эти нарушения периодичности вызывают рассеяние электронов. Электрическое сопротивление металлов возрастает с температурой, так как чем выше температура, тем интенсивнее колебания решетки. При низкой температуре, ~ 10 К, сопротивление определяется только рассеянием на дефектах структуры.

Удельное сопротивление 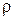металла, содержащего примесные атомы, можно записать в виде суммы:

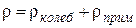, (3.13)

где 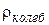– часть удельного сопротивления, обусловленная тепловым движением атомов решетки, а 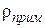– часть, обусловленная рассеянием электронов на примесных атомах.

Если концентрация примесных атомов невелика, то часть 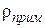оказывается не зависящей от температуры. Это утверждение называется правилом Матиссена.

Решеточный вклад в удельное сопротивление в металлах зависит от температуры по-разному. При высоких температурах 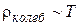. При низких температурах, то есть при ( 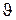– температура Дебая, при которой в твердом теле возбуждается весь спектр нормальных колебаний, включая колебание с максимально возможной частой), 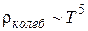. Линейная зависимость 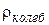от Т при высоких температурах есть следствие того факта, что вероятность рассеяния любого электрона пропорциональна числу фононов, которое 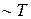. Слагаемое 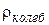уменьшается с понижением температуры и обращается в 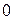при .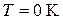

Таким образом, учитывая (3.1), находим:

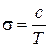, (3.14)

где 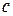– константа, зависящая от рода металла. Данное соотношение выполняется с высокой степенью точности для многих металлов в температурном диапазоне от 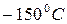до 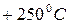. Зависимость 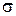от 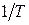представлена на рис. 3.5. Угол наклона прямой зависит от рода металла и .

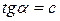Date: 2015-05-19; view: 726; Нарушение авторских прав