Основные теоретические положения. Явления, связанные с действием магнитного поля на электрические свойства металлов и полупроводников

Явления, связанные с действием магнитного поля 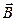на электрические свойства металлов и полупроводников, по которым течет электрический ток, называются гальваномагнитными явлениями. Различают два типа гальваномагнитных явлений: четные, зависящие от четных степеней 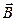, и нечетные, зависящие от нечетных степеней .

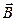Наиболее существенным из четных эффектов является изменение сопротивления в поперечном магнитном поле (эффект магнитосопротивления). Как показывает опыт, относительное изменение электропроводности 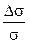при не очень сильных полях выражается формулой

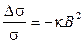, (3.1)

где 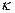– коэффициент магнитосопротивления, зависящий от свойств материала. Впервые существенное изменение сопротивления под действием магнитного поля было получено Капицей П.Л. (1927 г.).

Наиболее важным из нечетных эффектов является эффект Холла. Этот эффект, открытый Холлом в 1879 году, представляет собой явление возникновения разности потенциалов в направлении, перпендикулярном магнитному полю и току.

Физическая сущность всех этих явлений состоит в том, что внешнее поле 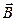влияет на траектории носителей тока в металлах и полупроводниках.

Существование эффекта Холла может быть объяснено следующим образом.

Если проводящую пластинку, вдоль которой течет ток 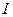поместить в перпендикулярное к ней магнитное поле 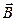, то между точками 1 и 2, расположенными на противоположных сторонах пластинки, возникает разность потенциалов 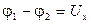. Опыт показывает, что

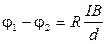, (3.2)

где 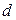– толщина пластинки, R – постоянная Холла.

Эффект Холла объясняется существованием силы Лоренца, действующей на электрический заряд 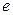, движущийся в магнитном поле

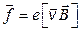, (3.3)

где 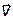– скорость движения заряда.

Плотность тока 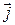и поле 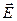связаны соотношением

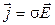(3.4)

где 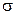– проводимость проводника.

Под действием силы Лоренца заряды будут перемещаться в поперечном току направлении, в результате чего на противоположных гранях образца возникнут избыточные заряды противоположных знаков. Они создадут поперечное электрическое поле 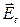, в котором действует сила

.

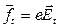Движение зарядов прекратится, когда сила, действующая на заряд, уравновесит силу Лоренца:

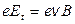. (3.5)

С другой стороны, средняя скорость направленного движения электронов в проводнике связана с плотностью тока 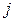уравнением

, (3.6)

где 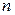– число электронов в единице объема. Комбинируя уравнения (3.5) и (3.6), можем исключить 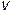, получим:

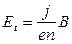. (3.7)

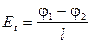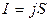Так как , а , где 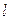– длина, а 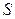– поперечное сечение бруска, то

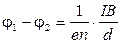. (3.8)

Сравнивая соотношения (3.2) и (3.8), получаем для постоянной Холла

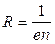. (3.9)

Рассмотрим элементарную теорию эффекта Холла в примесных полупроводниках с проводимостью одного типа (p - или n -). Образец полупроводника в виде прямоугольного бруска показан на рис.3.1.

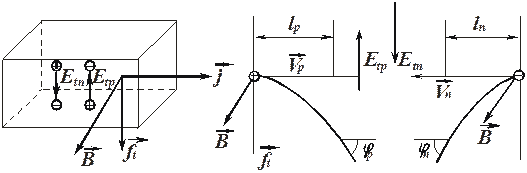
Пусть ток протекает слева направо. Если ток создается дырками, то скорость направленного движения дырок 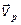имеет то же направление, что и ток, если же электронами, то их скорость 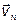направлена в противоположную сторону. Поместим полупроводник во внешнее магнитное поле 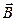. Для дырок сила Лоренца в случае, показанном на рис. 3.1, будет направ­ле­на вниз; такое же направление силы Лоренца будет и для электронов. Следовательно, как дырки, так и электроны, будут отклоняться магнитным полем на нижнюю грань, а верхняя грань будет обедняться в первом случае дырками, во втором – электронами.

Таким образом, в полупроводнике p -типа нижняя грань зарядится положительно, а верхняя – отрицательно, и возникает электрическое поле 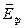, направленное снизу вверх. В полупроводнике n -типа нижняя грань при этом же направлении тока заряжается отрицательно, верхняя – положительно, и возникающее поле 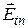направлено сверху вниз.

Положения дырки и электрона, отклоненных магнитным полем при дрейфовом перемещении дырки (электрона) на протяжении длины свободного пробега 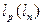, показаны на рис. 3.2. При этом предполагается, что поле 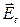еще отсутствует. Углы 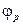и 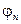называют углами Холла.

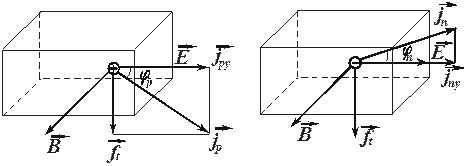
Если изобразить векторы плотности тока дырок и электронов, то, учитывая направления поворотов 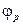и 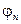, имеем, что плотности тока 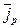и 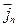поворачиваются в противоположные стороны (рис. 3.3).

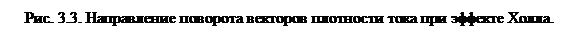
Накопление зарядов, отклоненных магнитным полем на противоположных гранях, происходит до тех пор, пока сила 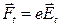не уравновесит силу Лоренца (3.3). Записав это условие равновесия и преобразовав его так же, как соотношение (3.5), получим следующие выражения для коэффициентов Холла:

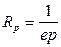– для полупроводников p -типа,

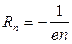– для полупроводников n -типа.

Здесь n, p – концентрации электронов и дырок в n - и p -полупроводниках соответственно.

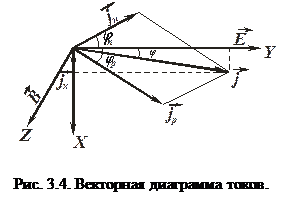Рассмотрим полупроводник с собственной электропроводностью. Векторы плотности токов дырок и электронов 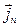отклоняются внешним магнитным полем в разные стороны, поэтому для такого полупроводника необходимо изображать векторную диаграмму токов (рис. 3.4). На этой диаграмме холловское поле 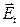еще не действует.

Полная плотность тока 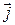является векторной суммой плотностей токов 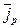и 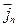и составляет угол 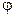с направлением внешнего поля 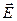, создающего дрейф носителей заряда. Следовательно,

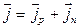. (3.10)

Выберем оси координат так, чтобы ось x была направлена по холловскому полю 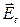или против него; ось y – по внешнему полю 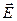, ось z – по магнитному полю .

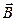Тогда, для малого угла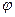

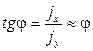. (3.11)

В соответствии с рис. 3.4

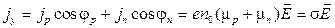. (3.12)

В выражении (3.12) учтено, что в полупроводнике с собственной проводимостью 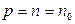, 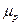и 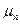– подвижности дырок и электронов соответственно. (Подвижность свободных носителей заряда численно равна средней скорости направленного движения, которую они приобретают в электрическом поле единичной напряженности). Здесь, считая углы 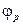и 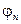малыми, то есть, рассматривая слабые магнитные поля, положили 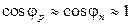. Тогда

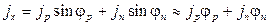, (3.13)

причем

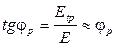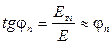, . (3.14)

Величину 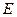можно выразить следующим образом:

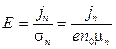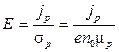, . (3.15)

Согласно (3.7)

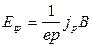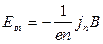, . (3.16)

Следовательно,

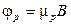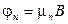, . (3.17)

Подставляя (3.17) в (3.13), получим:

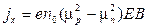. (3.18)

Холловское поле 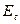можно определить из соотношения:

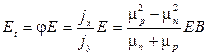. (3.19)

Кроме того, по формуле (3.7) имеем

. (3.20)

Сравнивая соотношения (3.19) и (3.20), получим

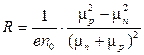, (3.21)

где .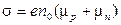

Date: 2015-05-19; view: 668; Нарушение авторских прав