
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Квантовая механика_рус.rtf. Понятие тождественные частицы:
|
|
$$$001
Понятие тождественные частицы:
A) вводится для описания любых многочастичных систем
B) не требует введения спина для лептонов и барионов
C) отражает неразличимость микрочастиц с одинаковыми характеристиками
D) можно ввести только для связанных систем – атомов, атомных ядер
E) не имеет аналога в макромире
F) применимо только к виртуальным элементарным частицам
G) связано с принципом неопределенности Гейзенберга
H) применимо, например, к бильярдным шарам одного цвета, размера
{ Правильный ответ} = C, E, G
{Сложность} = 1
{Учебник} = Давыдов А.С. Квантовая механика. Санкт-Петербург: 2011. 703 с.
{Характеристика} =
{Курс} =4
{Семестр} = 7
$$$002
Принцип тождественности на примере двух тождественных частиц:
A) при замене 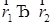 справедливо утверждение
справедливо утверждение 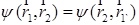
B) перестановка частиц не связана с заменой 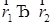
C) при перестановке двух частиц нарушается изотропность пространства
D) плотность вероятности 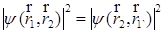
E) не учитывает спиновые характеристики частиц
F) свойства пространства не изменятся при перестановке двух частиц
G) замена переменных 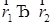 эквивалентна операции отражения
эквивалентна операции отражения
H) перестановка частиц эквивалентна замене 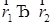
{ Правильный ответ} = D, F, H
{Сложность} = 1
{Учебник} = Давыдов А.С. Квантовая механика. Санкт-Петербург: 2011. 703 с.
{Характеристика} =
{Курс} =4
{Семестр} = 7
$$$003
Оператор перестановки частиц в координатном пространстве 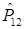 :
:
A) 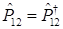 – эрмитов
– эрмитов
B) не эрмитов
C) имеет 4 собственных значения 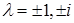
D) интеграл движения
E) 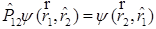
F) не сохраняется в переменных внешних полях
G) 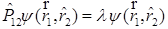 , собственные значения
, собственные значения 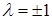
H) имеет собственные значения 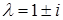
{ Правильный ответ} = A, E, G
{Сложность} = 2
{Учебник} = Давыдов А.С. Квантовая механика. Санкт-Петербург: 2011. 703 с.
{Характеристика} =
{Курс} =4
{Семестр} = 7
$$$004
Фермионы:
A) частицы с полуцелым спином – все адроны
B) 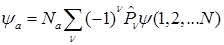 имеет нормировку
имеет нормировку 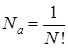
C) частицы с полуцелым спином – лептоны, барионы, кварки
D) 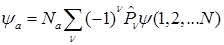 имеет нормировку
имеет нормировку 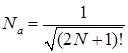
E) подчиняются статистике Бозе-Эйнштейна
F) подчиняются статистике Ферми-Дирака
G) 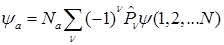 имеет нормировку
имеет нормировку 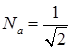
H) 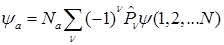 эквивалентна детерминанту Слэтера
эквивалентна детерминанту Слэтера
{ Правильный ответ} = C, F, H
{Сложность} = 2
{Учебник} = Давыдов А.С. Квантовая механика. Санкт-Петербург: 2011. 703 с.
{Характеристика} =
{Курс} =4
{Семестр} = 7
$$$005
Детерминант Слэтера 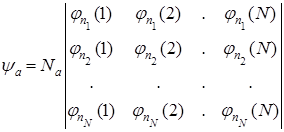 описывает систему из
описывает систему из 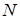 фермионов:
фермионов:
A) не меняет симметрию функции 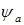 при отражении относительно диагонали
при отражении относительно диагонали
B) эквивалентен процедуре антисимметризации 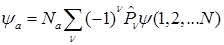
C) не эквивалентен процедуре антисимметризации 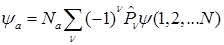
D) иллюстрирует принцип Паули
E) не меняет знак при перестановке двух столбцов
F) меняет знак при перестановке двух столбцов
G) при равенстве двух строк: 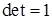
H) при равенстве двух строк: 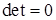
{ Правильный ответ} = B, D, H
{Сложность} = 2
{Учебник} = Давыдов А.С. Квантовая механика. Санкт-Петербург: 2011. 703 с.
{Характеристика} =
{Курс} =4
{Семестр} = 7
$$$006
Состояния фермиона с ориентацией спина 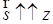 или
или 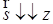 обозначим
обозначим 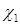 и
и 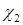 , соответственно. Спиновые волновые функции системы двух частиц со спиновыми квантовыми числами
, соответственно. Спиновые волновые функции системы двух частиц со спиновыми квантовыми числами 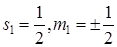 и
и 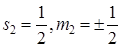 с учетом симметрии для суммарного спина
с учетом симметрии для суммарного спина 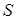 и его проекции
и его проекции 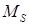 :
:
A) 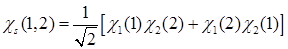 ,
, 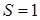 и
и 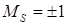
B) 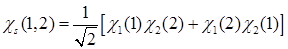 ,
, 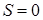 и
и 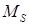 =0
=0
C) 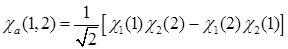 ,
, 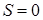 и
и 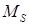 =0
=0
D) 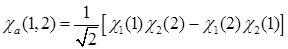 ,
, 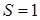 и
и 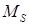 =0
=0
E) 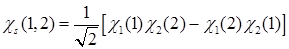 ,
, 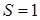 и
и 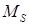 =0
=0
F) 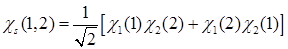 ,
, 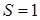 и
и 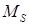 =0
=0
G) 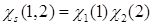 ,
, 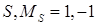 ;
; 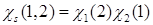 ,
, 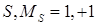
H) 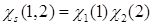 ,
, 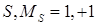 ;
; 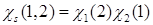 ,
, 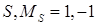
{ Правильный ответ} = C, F, H
{Сложность} = 2
{Учебник} = Давыдов А.С. Квантовая механика. Санкт-Петербург: 2011. 703 с.: стр.332-337.
{Характеристика} =
{Курс} =4
{Семестр} = 7
$$$007
Волновая функция для системы из трех частиц 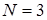 имеет
имеет 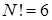 компонент, из которых строятся как симметричная функция
компонент, из которых строятся как симметричная функция 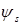 , так и антисимметричная
, так и антисимметричная 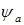 :
:
A) 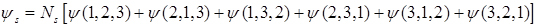
B) 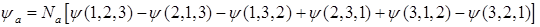
C) 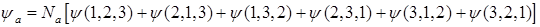
D) 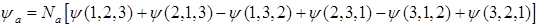
E) 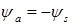
F) 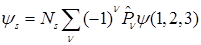 и
и 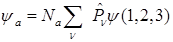
G) 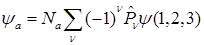 и
и 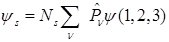
H) 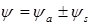 также имеет определенную симметрию
также имеет определенную симметрию
{ Правильный ответ} = A, B, G
{Сложность} = 3
{Учебник} = Давыдов А.С. Квантовая механика. Санкт-Петербург: 2011. 703 с.
{Характеристика} =
{Курс} =4
{Семестр} = 7
$$$008
Возбужденные состояния атома гелия соответствуют симметричной 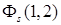 или антисимметричной
или антисимметричной 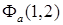 координатной волновой функции. С учетом спина полная волновая функция
координатной волновой функции. С учетом спина полная волновая функция 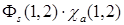 соответствует спину
соответствует спину 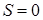 (парагелий);
(парагелий); 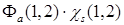 – соответствует спину
– соответствует спину 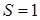 (ортогелий). Энергия складывается из энергии электронов
(ортогелий). Энергия складывается из энергии электронов 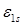 и
и 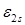 , кулоновской энергии взаимодействия
, кулоновской энергии взаимодействия 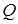 и обменной энергии
и обменной энергии 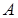 :
:
A) спиновые состояния не влияют на энергию пара- и орто-состояний
B) оба состояния имеют одинаковую энергию
C) спиновая симметрия влияет на энергию пара- и орто-состояний
D) для парагелия 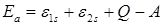
E) для ортогелия 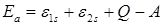
F) для ортогелия 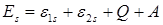
G) для парагелия 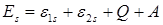
H) в этой системе не требуется учет принципа Паули
{ Правильный ответ} = C, E, G
{Сложность} = 3
{Учебник} = Давыдов А.С. Квантовая механика. Санкт-Петербург: 2011. 703 с.
{Характеристика} =
{Курс} =4
{Семестр} = 7
Date: 2015-05-19; view: 484; Нарушение авторских прав