
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Квантовая_механика_рус.rtf. Примеры операторов координаты, импульса и кинетической энергии в импульсном представлении:
|
|
$$$001
Примеры операторов координаты, импульса и кинетической энергии в импульсном представлении:
A) 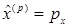
B) 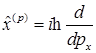
C) 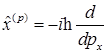
D) 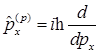
E) 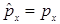
F) 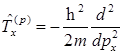
G) 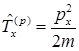
H) 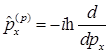
{ Правильный ответ} = B, E, G
{Сложность} = 1
{Учебник} = Давыдов А.С. Квантовая механика. Санкт-Петербург: 2011. 703 с.
{Характеристика}=
{Курс} = 4
{Семестр} = 7
$$$002
Определение матричных элементов оператора 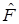 в явном виде и в обозначениях Дирака – элементов матрицы
в явном виде и в обозначениях Дирака – элементов матрицы 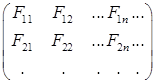 :
:
A) 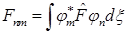
B) 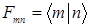
C) 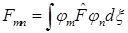
D) 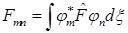
E) 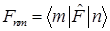
F) 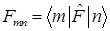
G) 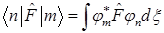
H) 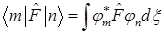
{ Правильный ответ} = D, F, H
{Сложность} = 1
{Учебник} = Давыдов А.С. Квантовая механика. Санкт-Петербург: 2011. 703 с.
{Характеристика}=
{Курс} = 4
{Семестр} = 7
$$$003
Коммутационные соотношения и операторные равенства в импульсном представлении:
A) 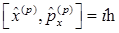
B) 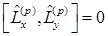
C) 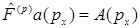
D) 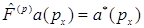
E) 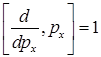
F) 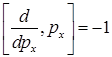
G) 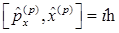
H) 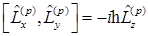
{ Правильный ответ} = A, C, E
{Сложность} = 1
{Учебник} = Давыдов А.С. Квантовая механика. Санкт-Петербург: 2011. 703 с.
{Характеристика}=
{Курс} = 4
{Семестр} = 7
$$$004
Волновые функции линейного гармонического осциллятора в импульсном представлении:
A) 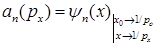
B) 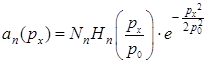 , где
, где 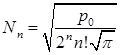
C) 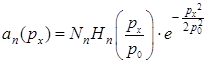 , где
, где 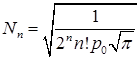
D) 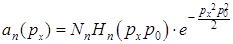 , где
, где 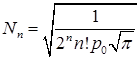
E) 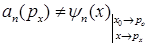
F) 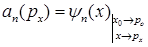
G) 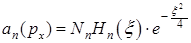
H) 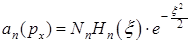
{ Правильный ответ} = C, F, H
{Сложность} = 1
{Учебник} = Давыдов А.С. Квантовая механика. Санкт-Петербург: 2011. 703 с.
{Характеристика}=
{Курс} = 4
{Семестр} = 7
$$$005
Уравнение Шредингера линейного гармонического осциллятора в безразмерных переменных 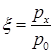 , где
, где 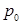 – осцилляторный параметр, и
– осцилляторный параметр, и 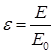 , где
, где 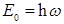 :
:
A) 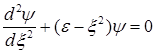 ,
, 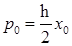
B) 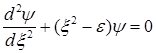 ,
, 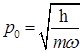
C) 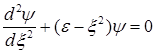 ,
, 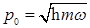
D) 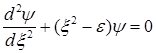 ,
, 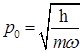
E) 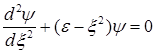 ,
, 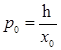
F) совпадает с безразмерным уравнением в координатном преставлении
G) не совпадает с безразмерным уравнением в координатном преставлении
H) 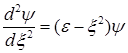 ,
, 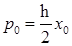
{ Правильный ответ} = C, E, F
{Сложность} = 2
{Учебник} = Давыдов А.С. Квантовая механика. Санкт-Петербург: 2011. 703 с.
{Характеристика}=
{Курс} = 4
{Семестр} = 7
$$$006
Уравнение Шредингера линейного гармонического осциллятора в импульсном представлении:
A) 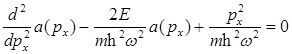
B) 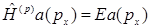
C) 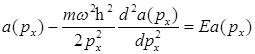
D) 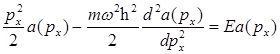
E) 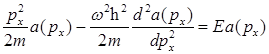
F) 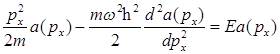
G) 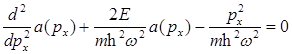
H) 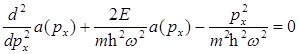
{ Правильный ответ} = B, F, H
{Сложность} = 2
{Учебник} = Давыдов А.С. Квантовая механика. Санкт-Петербург: 2011. 703 с.
{Характеристика}=
{Курс} = 4
{Семестр} = 7
$$$007
Для перехода к импульсному представлению в качестве базисных используются собственные функции оператора импульса 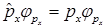 , так как они описывают движение свободной частицы, импульс
, так как они описывают движение свободной частицы, импульс 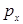 которой сохраняется. Спектр решений является непрерывным
которой сохраняется. Спектр решений является непрерывным 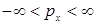 . Импульсное представление
. Импульсное представление 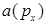 координатной функции
координатной функции 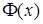 :
:
A) 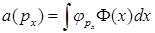
B) 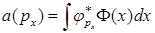
C) 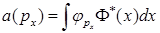
D) 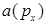 – это Фурье-образ функции
– это Фурье-образ функции 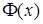
E) 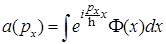
F) 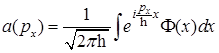
G) 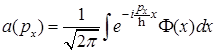
H) 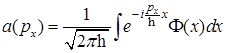
{ Правильный ответ} = B, D, H
{Сложность} = 2
{Учебник} = Давыдов А.С. Квантовая механика. Санкт-Петербург: 2011. 703 с.
{Характеристика}=
{Курс} = 4
{Семестр} = 7
$$$008
Для перехода к импульсному представлению в качестве базисных используются собственные функции оператора импульса 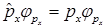 , так как они описывают движение свободной частицы, импульс
, так как они описывают движение свободной частицы, импульс 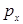 которой сохраняется. Спектр решений является непрерывным
которой сохраняется. Спектр решений является непрерывным 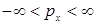 . Импульсное представление координатной функции
. Импульсное представление координатной функции 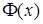 :
: 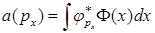 . Импульсное представление функции
. Импульсное представление функции 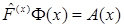 :
:
A) 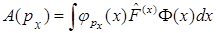
B) 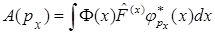
C) 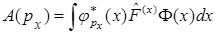
D) 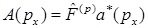
E) 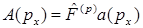
F) 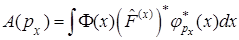 для эрмитовых операторов
для эрмитовых операторов
G) 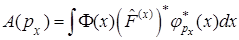 для любых операторов
для любых операторов
H) 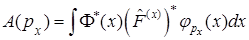
{ Правильный ответ} = C, E, F
{Сложность} = 2
{Учебник} = Давыдов А.С. Квантовая механика. Санкт-Петербург: 2011. 703 с.
{Характеристика}=
{Курс} = 4
{Семестр} = 7
$$$009
Основные свойства матричных элементов эрмитовых операторов:
A) 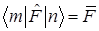
B) 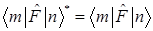 – действительные числа
– действительные числа
C) 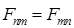
D) 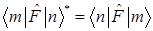
E) 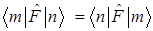
F) 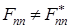
G) 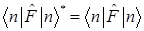 – действительные числа
– действительные числа
H) 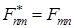
{ Правильный ответ} = D, G, H
{Сложность} = 2
{Учебник} = Давыдов А.С. Квантовая механика. Санкт-Петербург: 2011. 703 с.
{Характеристика}=
{Курс} = 4
{Семестр} = 7
$$$0010
Для расчета матричных элементов в представлении собственных функций линейного гармонического осциллятора используется рекуррентное соотношение 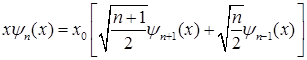 . Матричные элементы оператора
. Матричные элементы оператора 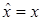 и правила отбора:
и правила отбора:
A) 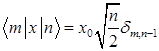
B) 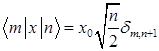
C) 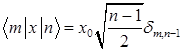
D) 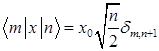
E) 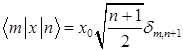
F) 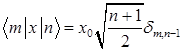
G) 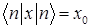
H) 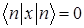
{ Правильный ответ} = A, E, H
{Сложность} = 3
{Учебник} = Давыдов А.С. Квантовая механика. Санкт-Петербург: 2011. 703 с.
{Характеристика}=
{Курс} = 4
{Семестр} = 7
$$$0011
Для расчета матричных элементов в представлении собственных функций линейного гармонического осциллятора используется рекуррентное соотношение 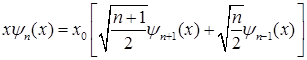 . Матричные элементы оператора
. Матричные элементы оператора 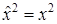 и правила отбора:
и правила отбора:
A) 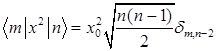
B) 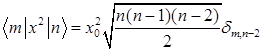
C) 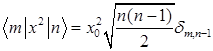
D) 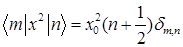
E) 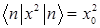
F) 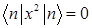
G) 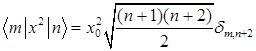
H) 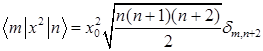
{ Правильный ответ} = A, D, G
{Сложность} = 3
{Учебник} = Давыдов А.С. Квантовая механика. Санкт-Петербург: 2011. 703 с.
{Характеристика}=
{Курс} = 4
{Семестр} = 7
$$$0012
В нерелятивистской квантовой механике оператор спина вводится через матрицы Паули 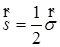 . Коммутационные свойства матриц Паули:
. Коммутационные свойства матриц Паули:
A) 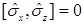
B) 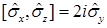
C) 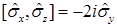
D) 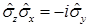
E) 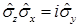
F) 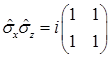
G) 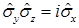
H) 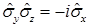
{ Правильный ответ} = C, E, G
{Сложность} = 3
{Учебник} = Давыдов А.С. Квантовая механика. Санкт-Петербург: 2011. 703 с.
{Характеристика}=
{Курс} = 4
{Семестр} = 7
Date: 2015-05-19; view: 709; Нарушение авторских прав