Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Решения задач
|
|
Задача 1.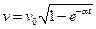 
, 
,
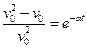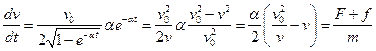. Откуда 
, 
.
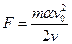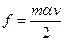Силы получены с точностью до некоторых функций скорости.
Ответ: , .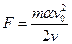
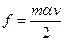Задача 2. Время, за которое вода преодолевает расстояние l равно t=l/v. За это время платформа повернется на угол a=wt=wl/v. Сила давления жидкости равно массовому расходу на нормальную составляющую относительной скорости F=g(vcos(a)-ωlsin(a)), момент M=Rtg(a)g(vcos(a)-ωlsin(a))=gvRtg(a)(cos(a)-asin(a))=gvRsin(a)(1-atg(a)).
Ответ: M= gvRsin(a)(1-atg(a)).
Задача 3. Запишем уравнение движения тела под действием силы трения F=kmg=armg
Учитывая, что l=r/cosα
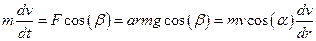, откуда 
.
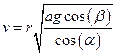Следовательно, угловая скорость w радиус-вектора r остается постоянной, постоянной и равной w должна оставаться угловая скорость вектора скорости v. (ω=vsin(a)/r)
Откуда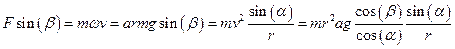 
. Далее 
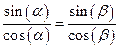, a=b, поэтому 
.
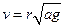Ответ: .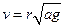
Задача 4. Момент инерции I=(maa2+mbb2)/3. Центр масс системы определяется вектором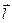 
.
, 
. 
.
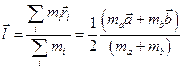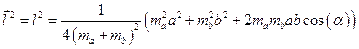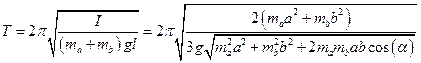Ответ: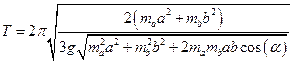 
.
Задача 5. Пусть минимальный объем равен V0, максимальный V. Рассмотрим два варианта: 1) p0V0=RT, 2p0V0=RTx, Tx=2T; 2) p0V=RT, 2p0V=RTx, Tx=2T.
Ответ: Tx=2T.
Задача 6. В силу цилиндрической симметрии диска относительно оси, распределим заряд на кольце путем вращения его вокруг оси по поверхности сферы радиуса R. Тогда поверхностная плотность заряда равна: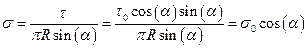 
, это распределение известно, оно создает однородное поле 
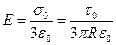, отсюда сила 
.
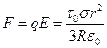Ответ: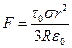 
.
Задача 7. Осевая составляющая поля первого соленоида равна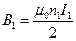 
, поток втекающий через торец второго соленоида равен 
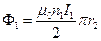. Этот поток вытекает через цилиндрическую поверхность второго соленоида. Вырежем кольцо толщиной dx из второго соленоида, на него действует сила ампера dF со стороны радиальной составляющей поля Br первого соленоида.
.
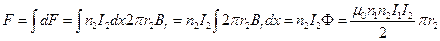Ответ: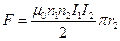 
.
Задача 8. Плоскую волну, при наличии рассеивающей линзы, можно заменить сферической волной от точечного источника, находящегося на расстоянии a от отверстия.При отсутствии отверстия интенсивность в точке наблюдения равна I0 /9. Радиус зон Френеля равен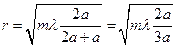 
, 
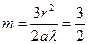. Интенсивность увеличится вдвое I = 2 I0 /9.
Ответ: I = 2 I0 /9.
Date: 2015-05-19; view: 348; Нарушение авторских прав