Решение задач. Задача 1. Сила тяги в начальный момент времени Fт=ma+c; при достижении максимальной скорости Fт=c+bvm; откуда ma+c=c+bvm и vm=ma/b

Задача 1. Сила тяги в начальный момент времени F_т=ma+c; при достижении максимальной скорости F_т=c+bv_m; откуда ma+c=c+bv_m и v_m=ma/b. Максимальное расстояние между автомобилями будет при достижении ими максимальных скоростей L=tv_m=tma/b.

Ответ: L=ma/b.

Задача 2. Движение происходит под действием силы сухого трения 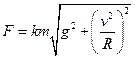. Уравнение динамики 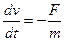. Уравнение кинематики 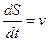. Исключаем время: 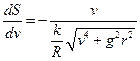Переменные делятся, решаем. Уравнение для определения величины v₀: 2pR = S(v₀), оно решается, 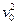=gRsh(4pk).

Ответ: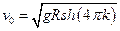

Задача 3. Пусть сила натяжения нити равна f. Уравнение тангенциального движения по окружности fsin(a)-F=0. Уравнение нормального движения по окружности f fcos(b)=mv²/r=mω²R. Тогда .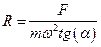

Ответ: .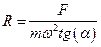

Задача 4. Особенность рассматриваемого цикла в том, что подвод тепла к рабочему телу и отвод тепла от рабочего тела происходит равномерно по времени, время подвода тепла и время отвода тепла одно и то же. В этом случае КПД цикла Карно .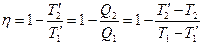

Из этих соотношений следует 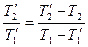. Находим 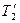, подставляем в выражение для работы цикла: 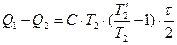, дифференцируем по 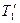, из условия максимума определяем этот параметр и подставляем в выражение для КПД, .

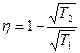Ответ: .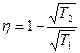

Задача 5. Уравнение движения по прямолинейной траектории под действием силы трения 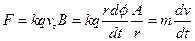. Откуда 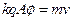и .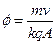

Ответ: .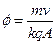

Задача 6. Из принципа суперпозиции во всех точках на срезе соленоида магнитное поле равно половине поля бесконечного соленоида, т.е. 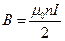, а поток 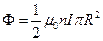. Вторая половина потока проходит через цилиндрическую поверхность.

Ответ: .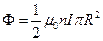

Задача 7. Рассмотрим рисунок к задаче. Если провести произвольную прямую из точки наблюдения под произвольным углом 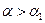и ещё такую же прямую под углом 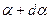, эти прямые вырежут отрезки «плоскостей» длиной dx и dX. Из подобия треугольников устанавливаем соотношение 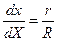, это расстояния до точки наблюдения. Определяя Н от одного и другого источника поля, убеждаемся, источники поля компенсируют друг друга.

Остаётся некомпенсированная часть нижней плоскости. Используем формулу для расчёта поля dН от бесконечной нити (дифференциал линейной координаты dX в этой области) и вычисляем проекции dH на х и на у. Заметим, что Rda/cos(a)=dX. Интегрируем полученные выражения 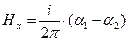, 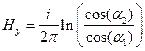- здесь получены абсолютные величины.

Ответ: , .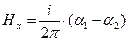

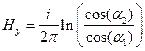Задача 8. Амплитуда волны с плоской поляризацией света: A_x=A₁cos²(a)-A₁/2, в перпендикулярной плоскости: A_y=A₁cos(a)sin(a). Результирующая интенсивность света: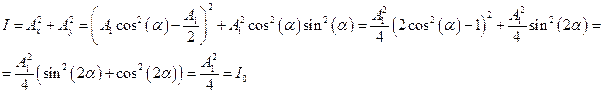

Ответ: I=I₀.

Date: 2015-05-19; view: 404; Нарушение авторских прав