Всероссийская олимпиада студентов по физике

III тур Всероссийской физической олимпиады студентов технических вузов прошел 16 мая 2013 года в Московском государственном техническом университете (МГТУ) им. Н.Э. Баумана.

Победители в командном зачете: команда Санкт-Петербургского государственного политехнического университета, набравшая 98 баллов - первое место, команда Калужского филиала Московского государственного технического университета им Н.Э. Баумана, набравшая 70 баллов - второе место, команда Московского института электронной техники, набравшая 67 баллов - третье место.

Победители в личном зачете: Авдеев Иван Дмитриевич, СПб ПТУ– первое место, Шубин Николай Михайлович, МИЭТ - второе место, Буряков Михаил Александрович, СПб ПТУ - третье место.

Задачи олимпиады:

Задача 1. Автомобиль массой m начинает движение. Определить зависимость силы тяги F и силы сопротивления f от скорости, если v зависит от времени следующим образом 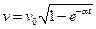, где v₀ и a - константы.

Задача 2. Горизонтальная платформа может вращаться относительно вертикальной оси. На оси симметрии платформы установлено горизонтально сопло, связанное с платформой, из которого вытекает вода cо скоростью v и массовым расходом g=dm/dt. На краю платформы установлен вертикально экран перпендикулярно оси струи на расстоянии R. Струя взаимодействует с экраном, растекаясь строго по поверхности без трения. Платформу начали вращать с угловой скоростью w. Определить момент силы, приложенный со стороны струи к экрану, если расстояние от сопла до точки касания струи с экраном при вращении стало равной l. Силой тяжести пренебречь.

Задача 3. Горизонтальная платформа вращается относительно вертикальной оси. По платформе от оси по спирали движется тело массы m так, что угол a между радиус-вектором и вектором скорости постоянен. Коэффициент трения между телом и платформой линейно зависит от радиуса k=ar. Определить зависимость скорости тела от радиуса r и величину угла между вектором скорости и вектором силы трения b.

Задача 4. Система состоит из двух однородных стержней, скрепленных у торцов (точка О) под углом a. Первый стержень имеет длину a и массу m_a, второй - b и m_b соответственно. Система совершает малые колебания относительно точки O в плоскости, проходящей через стержни. Определить период колебаний такой системы.

Задача 5. С одним киломолем газа совершается круговой процесс, состоящий из изохоры, изобары и адиабаты. Известно, что давление меняется в пределах от P₀ до 2P₀, а минимальная температура цикла равна T. Определить максимальную температуру цикла.

Задача 6. Кольцо радиуса R заряжено симметрично относительно оси, лежащей в плоскости кольца и проходящей через его центр. Линейная плотность заряда на кольце равна t=t₀cos(a)sin(a), где a - угол между осью и радиус вектором, проведенным из центра кольца. Внутри кольца находится диск радиуса r, равномерно заряженный поверхностным зарядом s, центр которого находится на оси, а плоскость перпендикулярна ей. Определить силу взаимодействия между диском и кольцом.

Задача 7. Определить силу взаимодействия между двумя длинными соленоидами, находящимися на одной оси, лежащие торцами на одной плоскости. Диаметры соленоидов равны r₁ и r₂, токи I₁ и I₂, плотности намотки n₁ и n₂.

Задача 8. Плоская световая волна l с интенсивностью I₀ падает нормально на круглое отверстие, в которое вставлена тонкая рассеивающая линза с фокусным расстоянием a. Какова интенсивность света в точке наблюдения, находящегося на оси системы на расстоянии 2а от отверстия, если радиус отверстия равен .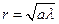

Date: 2015-05-19; view: 389; Нарушение авторских прав