Всероссийская олимпиада студентов по физике. II тур Всероссийской физической олимпиады студентов технических вузов прошел 23 марта 2013 года в Московском государственном техническом университете (МГТУ)

II тур Всероссийской физической олимпиады студентов технических вузов прошел 23 марта 2013 года в Московском государственном техническом университете (МГТУ) им. Н.Э. Баумана.

Победители в командном зачете: команда Московского государственного технического университета им. Н.Э.Баумана, набравшая 118 баллов - первое место, команда Московского авиационного института, набравшая 93 балла - второе место, команда Московского государственного университета нефти и газа им. И.М. Губкина, набравшая 89 баллов - третье место.

Победители в личном зачете: Никитин Иван Сергеевич МГТУ им. Н.Э. Баумана - первое место, Светличный Леонид Игоревич МИФИ (Обнинск) - второе место, Шубин Николай Михайлович МИЭТ - третье место.

Задачи олимпиады:

Задача 1. Два одинаковых автомобиля массы m начинают движение с постоянной тягой при сопротивлении движению, определяемому формулой F=c+bv, где v – текущая скорость, а c и b – константы. Отрезок времени между началом движения первого и второго автомобиля равен t. Определить максимальное расстояние между автомобилями в процессе дальнейшего движения, если известно, что начальное ускорение автомобилей равно a.

Задача 2. На проволочной окружности радиуса R, расположенной горизонтально, насажен небольшой шарик, который может двигаться по проволоке. С какой начальной скоростью надо толкнуть шарик вдоль проволоки, чтобы он сделал точно один оборот? Коэффициент трения скольжения равен k.

Задача 3. Газонокосилка типа «триммер» косит траву посредством невесомой нити, к концу которой привязан грузик массой m. Другой конец нити закреплен на роторе, вращающемся с угловой скоростью w, на расстоянии r от вертикальной оси вращения ротора. Угол между нитью и радиус-вектором грузика равен α. Определить радиус траектории грузика R, если сила сопротивления движению грузика постоянна и равна F.

Задача 4. Тепловая машина работает по циклу Карно, забирая тепло от нагревателя с температурой T₁ и отдавая его холодильнику с температурой T₂. Поток тепла между нагревателем и рабочим телом c температурой 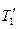пропорционален разности температур между ними 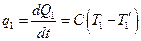, аналогично, поток тепла между рабочим телом с температурой 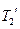и холодильником 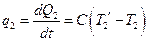. Считая, что изотермические процессы тепловой машины одинаковы по времени, а адиабатические процессы протекают мгновенно, определить КПД тепловой машины, когда ее мощность за цикл максимальна.

Задача 5. Частица массой m с зарядом q скользит в магнитном поле по горизонтальной плоскости, коэффициент трения с которой равен k. Вектор магнитного поля на всей траектории движения частицы направлен по радиусу r, проведенному из точки O, меняется по закону B = A/r и параллелен плоскости. Определить угол, на который повернется радиус-вектор частицы до полной остановки, если в начальный момент скорость частицы равна v. Силой тяжести пренебречь.

Задача 6. Определить поток магнитного поля через цилиндрическую поверхность полубесконечного соленоида радиуса R с плотностью намотки n, током I. Поле в выходном сечении соленоида считать однородным.

Задача 7. Две полубесконечные параллельные проводящие плоскости расположены напротив друг друга. По ним протекают вдоль границы полуплоскостей токи, равномерно распределенные по плоскости линейной плотностью i в противоположных направлениях. Определить магнитное поле в точке O, положение которой задается углами a₁ и a₂ между нормалью к плоскостям и нормалями к границам соответствующих плоскостей.

Задача 8. На пути плоскополяризованной световой волны интенсивности I₀ находится пластинка-поляризатор, закрывающая первую зону Френеля. Определить интенсивность света в точке наблюдения, если угол между плоскостью поляризации света и плоскостью поляризации поляризатора равен a.

Date: 2015-05-19; view: 522; Нарушение авторских прав